Assignment Problem: Meaning, Methods and Variations | Operations Research
After reading this article you will learn about:- 1. Meaning of Assignment Problem 2. Definition of Assignment Problem 3. Mathematical Formulation 4. Hungarian Method 5. Variations.

Meaning of Assignment Problem:
An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.
The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.
Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.
Definition of Assignment Problem:
ADVERTISEMENTS:
Suppose there are n jobs to be performed and n persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let c ij be the cost if the i-th person is assigned to the j-th job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.
The assignment problem can be stated in the form of n x n cost matrix C real members as given in the following table:
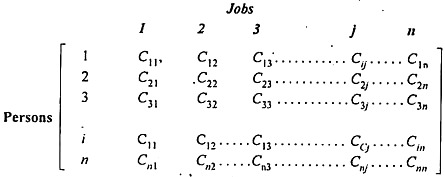
www.springer.com The European Mathematical Society
- StatProb Collection
- Recent changes
- Current events
- Random page
- Project talk
- Request account
- What links here
- Related changes
- Special pages
- Printable version
- Permanent link
- Page information
- View source
Assignment problem
The problem of optimally assigning $ m $ individuals to $ m $ jobs. It can be formulated as a linear programming problem that is a special case of the transport problem :
maximize $ \sum _ {i,j } c _ {ij } x _ {ij } $
$$ \sum _ { j } x _ {ij } = a _ {i} , i = 1 \dots m $$
(origins or supply),
$$ \sum _ { i } x _ {ij } = b _ {j} , j = 1 \dots n $$
(destinations or demand), where $ x _ {ij } \geq 0 $ and $ \sum a _ {i} = \sum b _ {j} $, which is called the balance condition. The assignment problem arises when $ m = n $ and all $ a _ {i} $ and $ b _ {j} $ are $ 1 $.
If all $ a _ {i} $ and $ b _ {j} $ in the transposed problem are integers, then there is an optimal solution for which all $ x _ {ij } $ are integers (Dantzig's theorem on integral solutions of the transport problem).
In the assignment problem, for such a solution $ x _ {ij } $ is either zero or one; $ x _ {ij } = 1 $ means that person $ i $ is assigned to job $ j $; the weight $ c _ {ij } $ is the utility of person $ i $ assigned to job $ j $.
The special structure of the transport problem and the assignment problem makes it possible to use algorithms that are more efficient than the simplex method . Some of these use the Hungarian method (see, e.g., [a5] , [a1] , Chapt. 7), which is based on the König–Egervary theorem (see König theorem ), the method of potentials (see [a1] , [a2] ), the out-of-kilter algorithm (see, e.g., [a3] ) or the transportation simplex method.
In turn, the transportation problem is a special case of the network optimization problem.
A totally different assignment problem is the pole assignment problem in control theory.
| [a1] | D.B. Yudin, E.G. Gol'shtein, "Linear programming" , Israel Program Sci. Transl. (1965) (In Russian) |
| [a2] | R. Frisch, "La résolution des problèmes de programme linéaire par la méthode du potentiel logarithmique" , (1956) pp. 20–23 |
| [a3] | K. Murtz, "Linear and combinatorial programming" , Wiley (1976) |
| [a4] | M. Grötschel, L. Lovász, A. Schrijver, "Geometric algorithms and combinatorial optimization" , Springer (1987) |
| [a5] | C.H. Papadimitriou, K. Steiglitz, "Combinatorial optimization" , Prentice-Hall (1982) |
- This page was last edited on 5 April 2020, at 18:48.
- Privacy policy
- About Encyclopedia of Mathematics
- Disclaimers
- Impressum-Legal
Algorithms: The Assignment Problem
One of the interesting things about studying optimization is that the techniques show up in a lot of different areas. The “assignment problem” is one that can be solved using simple techniques, at least for small problem sizes, and is easy to see how it could be applied to the real world.
Assignment Problem
Pretend for a moment that you are writing software for a famous ride sharing application. In a crowded environment, you might have multiple prospective customers that are requesting service at the same time, and nearby you have multiple drivers that can take them where they need to go. You want to assign the drivers to the customers in a way that minimizes customer wait time (so you keep the customers happy) and driver empty time (so you keep the drivers happy).
The assignment problem is designed for exactly this purpose. We start with m agents and n tasks. We make the rule that every agent has to be assigned to a task. For each agent-task pair, we figure out a cost associated to have that agent perform that task. We then figure out which assignment of agents to tasks minimizes the total cost.
Of course, it may be true that m != n , but that’s OK. If there are too many tasks, we can make up a “dummy” agent that is more expensive than any of the others. This will ensure that the least desirable task will be left to the dummy agent, and we can remove that from the solution. Or, if there are too many agents, we can make up a “dummy” task that is free for any agent. This will ensure that the agent with the highest true cost will get the dummy task, and will be idle.
If that last paragraph was a little dense, don’t worry; there’s an example coming that will help show how it works.
There are special algorithms for solving assignment problems, but one thing that’s nice about them is that a general-purpose solver can handle them too. Below is an example, but first it will help to cover a few concepts that we’ll be using.
Optimization Problems
Up above, we talked about making “rules” and minimizing costs. The usual name for this is optimization. An optimization problem is one where we have an “objective function” (which tells us what our goals are) and one or more “constraint functions” (which tell us what the rules are). The classic example is a factory that can make both “widgets” and “gadgets”. Each “widget” and “gadget” earns a certain amount of profit, but it also uses up raw material and time on the factory’s machines. The optimization problem is to determine exactly how many “widgets” and how many “gadgets” to make to maximize profit (the objective) while fitting within the material and time available (the constraints).
If we were to write this simple optimization problem out, it might look like this:
In this case, we have two variables: g for the number of gadgets we make and w for the number of widgets we make. We also have three constraints that we have to meet. Note that they are inequalities; we might not use all the available material or time in our optimal solution.
Just to unpack this a little: in English, the above is saying that we make 45 dollars / euros / quatloos per gadget we make. However, to make a gadget needs 120 lbs of raw material 1, 80 lbs of raw material 2, and 3.8 hours of machine time. So there is a limit on how many gadgets we can make, and it might be a better use of resources to balance gadgets with widgets.
Of course, real optimization problems have many more than two variables and many constraint functions, making them much harder to solve. The easiest kind of optimization problem to solve is linear, and fortunately, the assignment problem is linear.
Linear Programming
A linear program is a kind of optimization problem where both the objective function and the constraint functions are linear. (OK, that definition was a little self-referential.) We can have as many variables as we want, and as many constraint functions as we want, but none of the variables can have exponents in any of the functions. This limitation allows us to apply very efficient mathematical approaches to solve the problem, even for very large problems.
We can state the assignment problem as a linear programming problem. First, we choose to make “i” represent each of our agents (drivers) and “j” to represent each of our tasks (customers). Now, to write a problem like this, we need variables. The best approach is to use “indicator” variables, where xij = 1 means “driver i picks up customer j” and xij = 0 means “driver i does not pick up customer j”.
We wind up with:
This is a compact mathematical way to describe the problem, so again let me put it in English.
First, we need to figure out the cost of having each driver pick up each customer. Then, we can calculate the total cost for any scenario by just adding up the costs for the assignments we pick. For any assignment we don’t pick, xij will equal zero, so that term will just drop out of the sum.
Of course, the way we set up the objective function, the cheapest solution is for no drivers to pick up any customers. That’s not a very good business model. So we need a constraint to show that we want to have a driver assigned to every customer. At the same time, we can’t have a driver assigned to mutiple customers. So we need a constraint for that too. That leads us to the two constraints in the problem. The first just says, if you add up all the assignments for a given driver, you want the total number of assignments for that driver to be exactly one. The second constraint says, if you add up all the assignments to a given customer, you want the total number of drivers assigned to the customer to be one. If you have both of these, then each driver is assigned to exactly one customer, and the customers and drivers are happy. If you do it in a way that minimizes costs, then the business is happy too.
Solving with Octave and GLPK
The GNU Linear Programming Kit is a library that solves exactly these kinds of problems. It’s easy to set up the objective and constraints using GNU Octave and pass these over to GLPK for a solution.
Given some made-up sample data, the program looks like this:
Start with the definition of “c”, the cost information. For this example, I chose to have four drivers and three customers. There are sixteen numbers there; the first four are the cost of each driver to get the first customer, the next four are for the second customer, and the next four are for the third customer. Because we have an extra driver, we add a “dummy” customer at the end that is zero cost. This represents one of the drivers being idle.
The next definition is “b”, the right-hand side of our constraints. There are eight constraints, one for each of the drivers, and one for each of the customers (including the dummy). For each constraint, the right-hand side is 1.
The big block in the middle defines our constraint matrix “a”. This is the most challenging part of taking the mathematical definition and putting it into a form that is usable by GLPK; we have to expand out each constraint. Fortunately, in these kinds of cases, we tend to get pretty patterns that help us know we’re on the right track.
The first line in “a” says that the first customer needs a driver. To see why, remember that in our cost information, the first four numbers are the cost for each driver to get the first customer. With this constraint, we are requiring that one of those four costs be included and therefore that a driver is “selected” for the first customer. The other lines in “a” work similarly; the last four ensure that each driver has an assignment.
Note that the number of rows in “a” matches the number of items in “b”, and the number of columns in “a” matches the number of items in “c”. This is important; GLPK won’t run if this is not true (and our problem isn’t stated right in any case).
Compared to the above, the last few lines are easy.
- “lb” gives the lower bound for each variable.
- “ub” gives the upper bound.
- “ctype” tells GLPK that each constraint is an equality (“strict” as opposed to providing a lower or upper bound).
- “vartype” tells GLPK that these variables are all integers (can’t have half a driver showing up).
- “s” tells GLPK that we want to minimize our costs, not maximize them.
We push all that through a function call to GLPK, and what comes back are two values (along with some other stuff I’ll exclude for clarity):
The first item tells us that our best solution takes 27 minutes, or dollars, or whatever unit we used for cost. The second item tells us the assignments we got. (Note for pedants: I transposed this output to save space.)
This output tells us that customer 1 gets driver 2, customer 2 gets driver 3, customer 3 gets driver 4, and driver 1 is idle. If you look back at the cost data, you can see this makes sense, because driver 1 had some of the most expensive times to the three customers. You can also see that it managed to pick the least expensive pairing for each customer. (Of course, if I had done a better job making up cost data, it might not have picked the least expensive pairing in all cases, because a suboptimal individual pairing might still lead to an overall optimal solution. But this is a toy example.)
Of course, for a real application, we would have to take into consideration many other factors, such as the passage of time. Rather than knowing all of our customers and drivers up front, we would have customers and drivers continually showing up and being assigned. But I hope this simple example has revealed some of the concepts behind optimization and linear programming and the kinds of real-world problems that can be solved.
Quantitative Techniques: Theory and Problems by P. C. Tulsian, Vishal Pandey
Get full access to Quantitative Techniques: Theory and Problems and 60K+ other titles, with a free 10-day trial of O'Reilly.
There are also live events, courses curated by job role, and more.
WHAT IS ASSIGNMENT PROBLEM
Assignment Problem is a special type of linear programming problem where the objective is to minimise the cost or time of completing a number of jobs by a number of persons.
The assignment problem in the general form can be stated as follows:
“Given n facilities, n jobs and the effectiveness of each facility for each job, the problem is to assign each facility to one and only one job in such a way that the measure of effectiveness is optimised (Maximised or Minimised).”
Several problems of management has a structure identical with the assignment problem.
Example I A manager has four persons (i.e. facilities) available for four separate jobs (i.e. jobs) and the cost of assigning (i.e. effectiveness) each job to each ...
Get Quantitative Techniques: Theory and Problems now with the O’Reilly learning platform.
O’Reilly members experience books, live events, courses curated by job role, and more from O’Reilly and nearly 200 top publishers.
Don’t leave empty-handed
Get Mark Richards’s Software Architecture Patterns ebook to better understand how to design components—and how they should interact.
It’s yours, free.

Check it out now on O’Reilly
Dive in for free with a 10-day trial of the O’Reilly learning platform—then explore all the other resources our members count on to build skills and solve problems every day.


- Google OR-Tools
- Español – América Latina
- Português – Brasil
- Tiếng Việt
Solving an Assignment Problem
This section presents an example that shows how to solve an assignment problem using both the MIP solver and the CP-SAT solver.
In the example there are five workers (numbered 0-4) and four tasks (numbered 0-3). Note that there is one more worker than in the example in the Overview .
The costs of assigning workers to tasks are shown in the following table.
| Worker | Task 0 | Task 1 | Task 2 | Task 3 |
|---|---|---|---|---|
| 90 | 80 | 75 | 70 | |
| 35 | 85 | 55 | 65 | |
| 125 | 95 | 90 | 95 | |
| 45 | 110 | 95 | 115 | |
| 50 | 100 | 90 | 100 |
The problem is to assign each worker to at most one task, with no two workers performing the same task, while minimizing the total cost. Since there are more workers than tasks, one worker will not be assigned a task.
MIP solution
The following sections describe how to solve the problem using the MPSolver wrapper .
Import the libraries
The following code imports the required libraries.

Create the data
The following code creates the data for the problem.
The costs array corresponds to the table of costs for assigning workers to tasks, shown above.
Declare the MIP solver
The following code declares the MIP solver.
Create the variables
The following code creates binary integer variables for the problem.
Create the constraints
Create the objective function.
The following code creates the objective function for the problem.
The value of the objective function is the total cost over all variables that are assigned the value 1 by the solver.
Invoke the solver
The following code invokes the solver.
Print the solution
The following code prints the solution to the problem.
Here is the output of the program.
Complete programs
Here are the complete programs for the MIP solution.
CP SAT solution
The following sections describe how to solve the problem using the CP-SAT solver.
Declare the model
The following code declares the CP-SAT model.
The following code sets up the data for the problem.
The following code creates the constraints for the problem.
Here are the complete programs for the CP-SAT solution.
Except as otherwise noted, the content of this page is licensed under the Creative Commons Attribution 4.0 License , and code samples are licensed under the Apache 2.0 License . For details, see the Google Developers Site Policies . Java is a registered trademark of Oracle and/or its affiliates.
Last updated 2024-08-28 UTC.
The assignment problem as a cooperative game
- Published: 28 August 2024
Cite this article

- V. V. Morozov 1 &
- S. I. Romanov 1
We consider the problem of optimal distribution of assignments between workers on machines. Workers can exchange machines with the aim of saving the total time to execute the assignments, compared to their initial distribution. It is proved that the corresponding cooperative game has a non-empty c -core and is totally balanced. Based on the Hungarian method of solving the assignment problem, an algorithm for constructing an imputation from the c -core is formulated. In the case of an integer characteristic function, the algorithm constructs an imputation from the c -core with integer components. This result is generalized to the case of arbitrary totally balanced games of three and four persons, as well as for symmetric games.
This is a preview of subscription content, log in via an institution to check access.
Access this article
Subscribe and save.
- Get 10 units per month
- Download Article/Chapter or eBook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
Price includes VAT (Russian Federation)
Instant access to the full article PDF.
Rent this article via DeepDyve
Institutional subscriptions
Mazalov, V.V.: Matematicheskaya teoriya igr i prilozheniya [in Russian] (Mathematical game theory and applications). Lan, Saint-Petersburg (2010)
Google Scholar
Peleg, B., Sudhölter, P.: Introduction to the theory of cooperative games. Springer-Verlag, Berlin (2007)
Bondareva, O.N.: Nekotorye primeneniya metodov lineynogo programmirovaniya k teorii kooperativnyh igr [in Russian] (Some applications of linear programming methods to the theory of cooperative games). Probl. Cybern. 10 , 119–140 (1963)
Shapley, L.S.: On balanced sets and cores. RM-4601-PR. The Rand Corporation, Santa Monica, California (1965)
Charnes, A., Kortanek, K.: On balanced sets, cores and programming. Cah. Centre Etudes Rech. Oper. 9 (1), 32–43 (1967)
MathSciNet Google Scholar
Vasin, A.A., Morozov, V.V.: Teoriya igr i modeli matematicheskoy ekonomiki [in Russian] (Game theory and models of mathematical economics). MAX Press, Moscow (2005)
Peleg, B.: An inductive method for constructing minimal balanced collections of finite sets. Nav. Res. Logist. Quart. 12 (2), 155–162 (1965)
Article MathSciNet Google Scholar
Raiser, G.D.: Combinatorial mathematics. Mir, Moscow (1966)
Kuhn, H.W.: The Hungarian method for the assignment problem. Nav. Res. Logist. Quart. 2 (1-2), 155–162 (1955)
Download references
Author information
Authors and affiliations.
Faculty of Computational Mathematics and Cybernetics, Lomonosov Moscow State University, Moscow, Russian Federation
V. V. Morozov & S. I. Romanov
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to V. V. Morozov .
Additional information
Translated from Prikladnaya Matematika i Informatika , No. 74, pp. 19–26, 2023
This article is a translation of the original article published in Russian in the journal Prikladnaya Matematika i Informatika . The translation was done with the help of an artificial intelligence machine translation tool, and subsequently reviewed and revised by an expert with knowledge of the field. Springer Nature works continuously to further the development of tools for the production of journals, books and on the related technologies to support the authors.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
Reprints and permissions
About this article
Morozov, V.V., Romanov, S.I. The assignment problem as a cooperative game. Comput Math Model (2024). https://doi.org/10.1007/s10598-024-09600-0
Download citation
Received : 06 May 2023
Accepted : 12 October 2023
Published : 28 August 2024
DOI : https://doi.org/10.1007/s10598-024-09600-0
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Optimal assignment problem
- Core of a cooperative game
- Hungarian method
- Directed multigraph
- Find a journal
- Publish with us
- Track your research

COMMENTS
The assignment problem is a fundamental combinatorial optimization problem. In its most general form, the problem is as follows: The problem instance has a number of agents and a number of tasks. Any agent can be assigned to perform any task, incurring some cost that may vary depending on the agent-task assignment.
An assignment problem is a case of optimizing the allocation of resources to activities based on their efficiency and cost. Learn the mathematical formulation, Hungarian method and a practical example of an assignment problem in operations research.
Problem 4. Job shop needs to assign 4 jobs to 4 workers. The cost of performing a job is a function of the skills of the workers. Table summarizes the cost of the assignments. Worker1 cannot do job3, and worker 3 cannot do job 4. Determine the optimal assignment using the Hungarian method. Job.
The assignment problem is a fundamental combinatorial optimization problem. In its most general form, the problem is as follows: The problem instance has a number of agents and a number of tasks. Any agent can be assigned to perform any task, incurring some cost that may vary depending on the agent-task assignment.
Title: "Cracking the Balanced Assignment Problem in Operations Research!"🔍 Uncover the secrets of the Balanced Assignment Problem in this quick guide to Ope...
Operations Research-Assignment Problems/Models (Part-1)In this part, students will learn about the fundamentals of assignment problems, definition and variou...
The assignment problem is one of the fundamental combinatorial optimization problems in the branch of optimization or operations research in mathematics. In an assignment problem, we must find a maximum matching that has the minimum weight in a weighted bipartite graph. The Assignment problem ...
The assignment problem is one of the special type of transportation problem for which more efficient (less-time consuming) solution method has been devised by KUHN (1956) and FLOOD (1956). The justification of the steps leading to the solution is based on theorems proved by Hungarian mathematicians KONEIG (1950) and EGERVARY (1953), hence the ...
Abstract. Having reached the 50th (golden) anniversary of the publication of Kuhn's seminal article on the solution of the classic assignment problem, it seems useful to take a look at the variety of models to which it has given birth. This paper is a limited survey of what appear to be the most useful of the variations of the assignment ...
The problem is a special form of the transportation problem and, as such, has an optimal solution in which each variable is either zero or one. The problem can be solved by the simplex method, but special assignment problem algorithms tend to be computationally more efficient.
The assignment problem arises when $ m = n $ and all $ a _ {i} $ and $ b _ {j} $ are $ 1 $. If all $ a _ {i} $ and $ b _ {j} $ in the transposed problem are integers, then there is an optimal solution for which all $ x _ {ij } $ are integers (Dantzig's theorem on integral solutions of the transport problem). In the assignment problem, for such ...
The assignment problem is important from a theoretical point of view because it appears as a subproblem of a vast number of combinatorial optimization problems , and its solution allows the development of algorithms to solve other combinatorial optimization problems.
Introduction. Although the name "assignment problem" seems to have first appeared in a 1952 paper by Votaw and Orden [69], what is generally recognized to be the beginning of the development of practical solution methods for and variations on the classic assignment problem (hereafter referred to as the AP) was the publication in 1955 of Kuhn's article on the Hungarian method for its ...
Chapter 17 The Assignment Problem 301 These problems are all examples of problems which may be solved as as-signment problems. In this chapter we will derive an efficient algorithm for solving assignment problems, and then discuss several problems which may be solved using this algorithm. The assignment problem will then be described in terms ...
The "assignment problem" is one that can be solved using simple techniques, at least for small problem sizes, and is easy to see how it could be applied to the real world. Assignment Problem Pretend for a moment that you are writing software for a famous ride sharing application. In a crowded environment, you might have multiple prospective ...
assignment problem occurs frequently in practice and is a basic problem in network flow theory since it can be reduced to a number of other problems, including the shortest path, weighted matching, transportation, and minimal cost flow [4]. Furthermore, a World Bank-funded review estimated that in the "Greater Cai-ro ...
Equivalent Assignment Problem c(x, y) 00312 01015 43330 00110 12204 cp(x, y) 3891510 41071614 913111910 813122013 175119 8 13 11 19 13 5 4 3 0 8 9 + 8 - 13 10 Reduced costs. For x # X, y # Y, define cp(x, y) = p(x) + c(x, y) - p(y). Observation 1. Finding a min cost perfect matching with reduced costs
From this, we could solve it as a transportation problem or as a linear program. However, we can also take advantage of the form of the problem and put together an algorithm that takes advantage of it- this is the Hungarian Algorithm. The Hungarian Algorithm The Hungarian Algorithm is an algorithm designed to solve the assignment problem. We ...
The assignment problem is a special case of the transportation problem, which in turn is a special case of the min-cost flow problem, so it can be solved using algorithms that solve the more general cases. Also, our problem is a special case of binary integer linear programming problem (which is NP-hard). But, due to the specifics of the ...
In this video, let us understand what is an assignment problem and what is its linear programming formulation.
Assignment Problem is a linear programming problem of assigning facilities to jobs to optimise a measure of effectiveness. Learn the general form, a specific example and how to solve it with Quantitative Techniques: Theory and Problems book.
The problem is to assign each worker to at most one task, with no two workers performing the same task, while minimizing the total cost. Since there are more workers than tasks, one worker will not be assigned a task. MIP solution. The following sections describe how to solve the problem using the MPSolver wrapper. Import the libraries
The assignment problem can be understood as the issue how decision rights are allocated to the agents and organizational subunits of a society. In this wide interpretation, the assignment problem refers to three different, albeit related phenomena: i) the allocation of property rights to individuals, i.e. households, and to firms, ii) the ...
We consider the problem of optimal distribution of assignments between workers on machines. Workers can exchange machines with the aim of saving the total time to execute the assignments, compared to their initial distribution. It is proved that the corresponding cooperative game has a non-empty c-core and is totally balanced. Based on the Hungarian method of solving the assignment problem, an ...