- FOR INSTRUCTOR
- FOR INSTRUCTORS

8.4.3 Hypothesis Testing for the Mean
$\quad$ $H_0$: $\mu=\mu_0$, $\quad$ $H_1$: $\mu \neq \mu_0$.
$\quad$ $H_0$: $\mu \leq \mu_0$, $\quad$ $H_1$: $\mu > \mu_0$.
$\quad$ $H_0$: $\mu \geq \mu_0$, $\quad$ $H_1$: $\mu \lt \mu_0$.
Two-sided Tests for the Mean:
Therefore, we can suggest the following test. Choose a threshold, and call it $c$. If $|W| \leq c$, accept $H_0$, and if $|W|>c$, accept $H_1$. How do we choose $c$? If $\alpha$ is the required significance level, we must have
- As discussed above, we let \begin{align}%\label{} W(X_1,X_2, \cdots,X_n)=\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}}. \end{align} Note that, assuming $H_0$, $W \sim N(0,1)$. We will choose a threshold, $c$. If $|W| \leq c$, we accept $H_0$, and if $|W|>c$, accept $H_1$. To choose $c$, we let \begin{align} P(|W| > c \; | \; H_0) =\alpha. \end{align} Since the standard normal PDF is symmetric around $0$, we have \begin{align} P(|W| > c \; | \; H_0) = 2 P(W>c | \; H_0). \end{align} Thus, we conclude $P(W>c | \; H_0)=\frac{\alpha}{2}$. Therefore, \begin{align} c=z_{\frac{\alpha}{2}}. \end{align} Therefore, we accept $H_0$ if \begin{align} \left|\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}} \right| \leq z_{\frac{\alpha}{2}}, \end{align} and reject it otherwise.
- We have \begin{align} \beta (\mu) &=P(\textrm{type II error}) = P(\textrm{accept }H_0 \; | \; \mu) \\ &= P\left(\left|\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}} \right| \lt z_{\frac{\alpha}{2}}\; | \; \mu \right). \end{align} If $X_i \sim N(\mu,\sigma^2)$, then $\overline{X} \sim N(\mu, \frac{\sigma^2}{n})$. Thus, \begin{align} \beta (\mu)&=P\left(\left|\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}} \right| \lt z_{\frac{\alpha}{2}}\; | \; \mu \right)\\ &=P\left(\mu_0- z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}} \leq \overline{X} \leq \mu_0+ z_{\frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}\right)\\ &=\Phi\left(z_{\frac{\alpha}{2}}+\frac{\mu_0-\mu}{\sigma / \sqrt{n}}\right)-\Phi\left(-z_{\frac{\alpha}{2}}+\frac{\mu_0-\mu}{\sigma / \sqrt{n}}\right). \end{align}
- Let $S^2$ be the sample variance for this random sample. Then, the random variable $W$ defined as \begin{equation} W(X_1,X_2, \cdots, X_n)=\frac{\overline{X}-\mu_0}{S / \sqrt{n}} \end{equation} has a $t$-distribution with $n-1$ degrees of freedom, i.e., $W \sim T(n-1)$. Thus, we can repeat the analysis of Example 8.24 here. The only difference is that we need to replace $\sigma$ by $S$ and $z_{\frac{\alpha}{2}}$ by $t_{\frac{\alpha}{2},n-1}$. Therefore, we accept $H_0$ if \begin{align} |W| \leq t_{\frac{\alpha}{2},n-1}, \end{align} and reject it otherwise. Let us look at a numerical example of this case.
$\quad$ $H_0$: $\mu=170$, $\quad$ $H_1$: $\mu \neq 170$.
- Let's first compute the sample mean and the sample standard deviation. The sample mean is \begin{align}%\label{} \overline{X}&=\frac{X_1+X_2+X_3+X_4+X_5+X_6+X_7+X_8+X_9}{9}\\ &=165.8 \end{align} The sample variance is given by \begin{align}%\label{} {S}^2=\frac{1}{9-1} \sum_{k=1}^9 (X_k-\overline{X})^2&=68.01 \end{align} The sample standard deviation is given by \begin{align}%\label{} S&= \sqrt{S^2}=8.25 \end{align} The following MATLAB code can be used to obtain these values: x=[176.2,157.9,160.1,180.9,165.1,167.2,162.9,155.7,166.2]; m=mean(x); v=var(x); s=std(x); Now, our test statistic is \begin{align} W(X_1,X_2, \cdots, X_9)&=\frac{\overline{X}-\mu_0}{S / \sqrt{n}}\\ &=\frac{165.8-170}{8.25 / 3}=-1.52 \end{align} Thus, $|W|=1.52$. Also, we have \begin{align} t_{\frac{\alpha}{2},n-1} = t_{0.025,8} \approx 2.31 \end{align} The above value can be obtained in MATLAB using the command $\mathtt{tinv(0.975,8)}$. Thus, we conclude \begin{align} |W| \leq t_{\frac{\alpha}{2},n-1}. \end{align} Therefore, we accept $H_0$. In other words, we do not have enough evidence to conclude that the average height in the city is different from the average height in the country.
Let us summarize what we have obtained for the two-sided test for the mean.
| Case | Test Statistic | Acceptance Region |
|---|---|---|
| $X_i \sim N(\mu, \sigma^2)$, $\sigma$ known | $W=\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}}$ | $|W| \leq z_{\frac{\alpha}{2}}$ |
| $n$ large, $X_i$ non-normal | $W=\frac{\overline{X}-\mu_0}{S / \sqrt{n}}$ | $|W| \leq z_{\frac{\alpha}{2}}$ |
| $X_i \sim N(\mu, \sigma^2)$, $\sigma$ unknown | $W=\frac{\overline{X}-\mu_0}{S / \sqrt{n}}$ | $|W| \leq t_{\frac{\alpha}{2},n-1}$ |
One-sided Tests for the Mean:
- As before, we define the test statistic as \begin{align}%\label{} W(X_1,X_2, \cdots,X_n)=\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}}. \end{align} If $H_0$ is true (i.e., $\mu \leq \mu_0$), we expect $\overline{X}$ (and thus $W$) to be relatively small, while if $H_1$ is true, we expect $\overline{X}$ (and thus $W$) to be larger. This suggests the following test: Choose a threshold, and call it $c$. If $W \leq c$, accept $H_0$, and if $W>c$, accept $H_1$. How do we choose $c$? If $\alpha$ is the required significance level, we must have \begin{align} P(\textrm{type I error}) &= P(\textrm{Reject }H_0 \; | \; H_0) \\ &= P(W > c \; | \; \mu \leq \mu_0) \leq \alpha. \end{align} Here, the probability of type I error depends on $\mu$. More specifically, for any $\mu \leq \mu_0$, we can write \begin{align} P(\textrm{type I error} \; | \; \mu) &= P(\textrm{Reject }H_0 \; | \; \mu) \\ &= P(W > c \; | \; \mu)\\ &=P \left(\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}}> c \; | \; \mu\right)\\ &=P \left(\frac{\overline{X}-\mu}{\sigma / \sqrt{n}}+\frac{\mu-\mu_0}{\sigma / \sqrt{n}}> c \; | \; \mu\right)\\ &=P \left(\frac{\overline{X}-\mu}{\sigma / \sqrt{n}}> c+\frac{\mu_0-\mu}{\sigma / \sqrt{n}} \; | \; \mu\right)\\ &\leq P \left(\frac{\overline{X}-\mu}{\sigma / \sqrt{n}}> c \; | \; \mu\right) \quad (\textrm{ since }\mu \leq \mu_0)\\ &=1-\Phi(c) \quad \big(\textrm{ since given }\mu, \frac{\overline{X}-\mu}{\sigma / \sqrt{n}} \sim N(0,1) \big). \end{align} Thus, we can choose $\alpha=1-\Phi(c)$, which results in \begin{align} c=z_{\alpha}. \end{align} Therefore, we accept $H_0$ if \begin{align} \frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}} \leq z_{\alpha}, \end{align} and reject it otherwise.
| Case | Test Statistic | Acceptance Region |
|---|---|---|
| $X_i \sim N(\mu, \sigma^2)$, $\sigma$ known | $W=\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}}$ | $W \leq z_{\alpha}$ |
| $n$ large, $X_i$ non-normal | $W=\frac{\overline{X}-\mu_0}{S / \sqrt{n}}$ | $W \leq z_{\alpha}$ |
| $X_i \sim N(\mu, \sigma^2)$, $\sigma$ unknown | $W=\frac{\overline{X}-\mu_0}{S / \sqrt{n}}$ | $W \leq t_{\alpha,n-1}$ |
$\quad$ $H_0$: $\mu \geq \mu_0$, $\quad$ $H_1$: $\mu \lt \mu_0$,
| Case | Test Statistic | Acceptance Region |
|---|---|---|
| $X_i \sim N(\mu, \sigma^2)$, $\sigma$ known | $W=\frac{\overline{X}-\mu_0}{\sigma / \sqrt{n}}$ | $W \geq -z_{\alpha}$ |
| $n$ large, $X_i$ non-normal | $W=\frac{\overline{X}-\mu_0}{S / \sqrt{n}}$ | $W \geq -z_{\alpha}$ |
| $X_i \sim N(\mu, \sigma^2)$, $\sigma$ unknown | $W=\frac{\overline{X}-\mu_0}{S / \sqrt{n}}$ | $W \geq -t_{\alpha,n-1}$ |
The print version of the book is available on . |
|
Have a language expert improve your writing
Run a free plagiarism check in 10 minutes, generate accurate citations for free.
- Knowledge Base
Hypothesis Testing | A Step-by-Step Guide with Easy Examples
Published on November 8, 2019 by Rebecca Bevans . Revised on June 22, 2023.
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics . It is most often used by scientists to test specific predictions, called hypotheses, that arise from theories.
There are 5 main steps in hypothesis testing:
- State your research hypothesis as a null hypothesis and alternate hypothesis (H o ) and (H a or H 1 ).
- Collect data in a way designed to test the hypothesis.
- Perform an appropriate statistical test .
- Decide whether to reject or fail to reject your null hypothesis.
- Present the findings in your results and discussion section.
Though the specific details might vary, the procedure you will use when testing a hypothesis will always follow some version of these steps.
Table of contents
Step 1: state your null and alternate hypothesis, step 2: collect data, step 3: perform a statistical test, step 4: decide whether to reject or fail to reject your null hypothesis, step 5: present your findings, other interesting articles, frequently asked questions about hypothesis testing.
After developing your initial research hypothesis (the prediction that you want to investigate), it is important to restate it as a null (H o ) and alternate (H a ) hypothesis so that you can test it mathematically.
The alternate hypothesis is usually your initial hypothesis that predicts a relationship between variables. The null hypothesis is a prediction of no relationship between the variables you are interested in.
- H 0 : Men are, on average, not taller than women. H a : Men are, on average, taller than women.
Here's why students love Scribbr's proofreading services
Discover proofreading & editing
For a statistical test to be valid , it is important to perform sampling and collect data in a way that is designed to test your hypothesis. If your data are not representative, then you cannot make statistical inferences about the population you are interested in.
There are a variety of statistical tests available, but they are all based on the comparison of within-group variance (how spread out the data is within a category) versus between-group variance (how different the categories are from one another).
If the between-group variance is large enough that there is little or no overlap between groups, then your statistical test will reflect that by showing a low p -value . This means it is unlikely that the differences between these groups came about by chance.
Alternatively, if there is high within-group variance and low between-group variance, then your statistical test will reflect that with a high p -value. This means it is likely that any difference you measure between groups is due to chance.
Your choice of statistical test will be based on the type of variables and the level of measurement of your collected data .
- an estimate of the difference in average height between the two groups.
- a p -value showing how likely you are to see this difference if the null hypothesis of no difference is true.
Based on the outcome of your statistical test, you will have to decide whether to reject or fail to reject your null hypothesis.
In most cases you will use the p -value generated by your statistical test to guide your decision. And in most cases, your predetermined level of significance for rejecting the null hypothesis will be 0.05 – that is, when there is a less than 5% chance that you would see these results if the null hypothesis were true.
In some cases, researchers choose a more conservative level of significance, such as 0.01 (1%). This minimizes the risk of incorrectly rejecting the null hypothesis ( Type I error ).
The results of hypothesis testing will be presented in the results and discussion sections of your research paper , dissertation or thesis .
In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p -value). In the discussion , you can discuss whether your initial hypothesis was supported by your results or not.
In the formal language of hypothesis testing, we talk about rejecting or failing to reject the null hypothesis. You will probably be asked to do this in your statistics assignments.
However, when presenting research results in academic papers we rarely talk this way. Instead, we go back to our alternate hypothesis (in this case, the hypothesis that men are on average taller than women) and state whether the result of our test did or did not support the alternate hypothesis.
If your null hypothesis was rejected, this result is interpreted as “supported the alternate hypothesis.”
These are superficial differences; you can see that they mean the same thing.
You might notice that we don’t say that we reject or fail to reject the alternate hypothesis . This is because hypothesis testing is not designed to prove or disprove anything. It is only designed to test whether a pattern we measure could have arisen spuriously, or by chance.
If we reject the null hypothesis based on our research (i.e., we find that it is unlikely that the pattern arose by chance), then we can say our test lends support to our hypothesis . But if the pattern does not pass our decision rule, meaning that it could have arisen by chance, then we say the test is inconsistent with our hypothesis .
If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.
- Normal distribution
- Descriptive statistics
- Measures of central tendency
- Correlation coefficient
Methodology
- Cluster sampling
- Stratified sampling
- Types of interviews
- Cohort study
- Thematic analysis
Research bias
- Implicit bias
- Cognitive bias
- Survivorship bias
- Availability heuristic
- Nonresponse bias
- Regression to the mean
Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.
A hypothesis states your predictions about what your research will find. It is a tentative answer to your research question that has not yet been tested. For some research projects, you might have to write several hypotheses that address different aspects of your research question.
A hypothesis is not just a guess — it should be based on existing theories and knowledge. It also has to be testable, which means you can support or refute it through scientific research methods (such as experiments, observations and statistical analysis of data).
Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.
Bevans, R. (2023, June 22). Hypothesis Testing | A Step-by-Step Guide with Easy Examples. Scribbr. Retrieved August 26, 2024, from https://www.scribbr.com/statistics/hypothesis-testing/
Is this article helpful?
Rebecca Bevans
Other students also liked, choosing the right statistical test | types & examples, understanding p values | definition and examples, what is your plagiarism score.

Hypothesis Testing for Means & Proportions
- 1
- | 2
- | 3
- | 4
- | 5
- | 6
- | 7
- | 8
- | 9
- | 10

Introduction to Hypothesis Testing
- Techniques for Hypothesis Testing
- General Approach:A Simple Example

All Modules

Z score Table
t score Table
Techniques for Hypothesis Testing
The techniques for hypothesis testing depend on
- the type of outcome variable being analyzed (continuous, dichotomous, discrete)
- the number of comparison groups in the investigation
- whether the comparison groups are independent (i.e., physically separate such as men versus women) or dependent (i.e., matched or paired such as pre- and post-assessments on the same participants).
In estimation we focused explicitly on techniques for one and two samples and discussed estimation for a specific parameter (e.g., the mean or proportion of a population), for differences (e.g., difference in means, the risk difference) and ratios (e.g., the relative risk and odds ratio). Here we will focus on procedures for one and two samples when the outcome is either continuous (and we focus on means) or dichotomous (and we focus on proportions).
General Approach: A Simple Example
The Centers for Disease Control (CDC) reported on trends in weight, height and body mass index from the 1960's through 2002. 1 The general trend was that Americans were much heavier and slightly taller in 2002 as compared to 1960; both men and women gained approximately 24 pounds, on average, between 1960 and 2002. In 2002, the mean weight for men was reported at 191 pounds. Suppose that an investigator hypothesizes that weights are even higher in 2006 (i.e., that the trend continued over the subsequent 4 years). The research hypothesis is that the mean weight in men in 2006 is more than 191 pounds. The null hypothesis is that there is no change in weight, and therefore the mean weight is still 191 pounds in 2006.
| Null Hypothesis | H : μ= 191 (no change) |
| Research Hypothesis | H : μ> 191 (investigator's belief) |
In order to test the hypotheses, we select a random sample of American males in 2006 and measure their weights. Suppose we have resources available to recruit n=100 men into our sample. We weigh each participant and compute summary statistics on the sample data. Suppose in the sample we determine the following:
Do the sample data support the null or research hypothesis? The sample mean of 197.1 is numerically higher than 191. However, is this difference more than would be expected by chance? In hypothesis testing, we assume that the null hypothesis holds until proven otherwise. We therefore need to determine the likelihood of observing a sample mean of 197.1 or higher when the true population mean is 191 (i.e., if the null hypothesis is true or under the null hypothesis). We can compute this probability using the Central Limit Theorem. Specifically,
(Notice that we use the sample standard deviation in computing the Z score. This is generally an appropriate substitution as long as the sample size is large, n > 30. Thus, there is less than a 1% probability of observing a sample mean as large as 197.1 when the true population mean is 191. Do you think that the null hypothesis is likely true? Based on how unlikely it is to observe a sample mean of 197.1 under the null hypothesis (i.e., <1% probability), we might infer, from our data, that the null hypothesis is probably not true.
Suppose that the sample data had turned out differently. Suppose that we instead observed the following in 2006:
How likely it is to observe a sample mean of 192.1 or higher when the true population mean is 191 (i.e., if the null hypothesis is true)? We can again compute this probability using the Central Limit Theorem. Specifically,
There is a 33.4% probability of observing a sample mean as large as 192.1 when the true population mean is 191. Do you think that the null hypothesis is likely true?
Neither of the sample means that we obtained allows us to know with certainty whether the null hypothesis is true or not. However, our computations suggest that, if the null hypothesis were true, the probability of observing a sample mean >197.1 is less than 1%. In contrast, if the null hypothesis were true, the probability of observing a sample mean >192.1 is about 33%. We can't know whether the null hypothesis is true, but the sample that provided a mean value of 197.1 provides much stronger evidence in favor of rejecting the null hypothesis, than the sample that provided a mean value of 192.1. Note that this does not mean that a sample mean of 192.1 indicates that the null hypothesis is true; it just doesn't provide compelling evidence to reject it.
In essence, hypothesis testing is a procedure to compute a probability that reflects the strength of the evidence (based on a given sample) for rejecting the null hypothesis. In hypothesis testing, we determine a threshold or cut-off point (called the critical value) to decide when to believe the null hypothesis and when to believe the research hypothesis. It is important to note that it is possible to observe any sample mean when the true population mean is true (in this example equal to 191), but some sample means are very unlikely. Based on the two samples above it would seem reasonable to believe the research hypothesis when x̄ = 197.1, but to believe the null hypothesis when x̄ =192.1. What we need is a threshold value such that if x̄ is above that threshold then we believe that H 1 is true and if x̄ is below that threshold then we believe that H 0 is true. The difficulty in determining a threshold for x̄ is that it depends on the scale of measurement. In this example, the threshold, sometimes called the critical value, might be 195 (i.e., if the sample mean is 195 or more then we believe that H 1 is true and if the sample mean is less than 195 then we believe that H 0 is true). Suppose we are interested in assessing an increase in blood pressure over time, the critical value will be different because blood pressures are measured in millimeters of mercury (mmHg) as opposed to in pounds. In the following we will explain how the critical value is determined and how we handle the issue of scale.
First, to address the issue of scale in determining the critical value, we convert our sample data (in particular the sample mean) into a Z score. We know from the module on probability that the center of the Z distribution is zero and extreme values are those that exceed 2 or fall below -2. Z scores above 2 and below -2 represent approximately 5% of all Z values. If the observed sample mean is close to the mean specified in H 0 (here m =191), then Z will be close to zero. If the observed sample mean is much larger than the mean specified in H 0 , then Z will be large.
In hypothesis testing, we select a critical value from the Z distribution. This is done by first determining what is called the level of significance, denoted α ("alpha"). What we are doing here is drawing a line at extreme values. The level of significance is the probability that we reject the null hypothesis (in favor of the alternative) when it is actually true and is also called the Type I error rate.
α = Level of significance = P(Type I error) = P(Reject H 0 | H 0 is true).
Because α is a probability, it ranges between 0 and 1. The most commonly used value in the medical literature for α is 0.05, or 5%. Thus, if an investigator selects α=0.05, then they are allowing a 5% probability of incorrectly rejecting the null hypothesis in favor of the alternative when the null is in fact true. Depending on the circumstances, one might choose to use a level of significance of 1% or 10%. For example, if an investigator wanted to reject the null only if there were even stronger evidence than that ensured with α=0.05, they could choose a =0.01as their level of significance. The typical values for α are 0.01, 0.05 and 0.10, with α=0.05 the most commonly used value.
Suppose in our weight study we select α=0.05. We need to determine the value of Z that holds 5% of the values above it (see below).

The critical value of Z for α =0.05 is Z = 1.645 (i.e., 5% of the distribution is above Z=1.645). With this value we can set up what is called our decision rule for the test. The rule is to reject H 0 if the Z score is 1.645 or more.
With the first sample we have
Because 2.38 > 1.645, we reject the null hypothesis. (The same conclusion can be drawn by comparing the 0.0087 probability of observing a sample mean as extreme as 197.1 to the level of significance of 0.05. If the observed probability is smaller than the level of significance we reject H 0 ). Because the Z score exceeds the critical value, we conclude that the mean weight for men in 2006 is more than 191 pounds, the value reported in 2002. If we observed the second sample (i.e., sample mean =192.1), we would not be able to reject the null hypothesis because the Z score is 0.43 which is not in the rejection region (i.e., the region in the tail end of the curve above 1.645). With the second sample we do not have sufficient evidence (because we set our level of significance at 5%) to conclude that weights have increased. Again, the same conclusion can be reached by comparing probabilities. The probability of observing a sample mean as extreme as 192.1 is 33.4% which is not below our 5% level of significance.
return to top | previous page | next page
Content ©2017. All Rights Reserved. Date last modified: November 6, 2017. Wayne W. LaMorte, MD, PhD, MPH
Hypothesis tests about the mean
by Marco Taboga , PhD
This lecture explains how to conduct hypothesis tests about the mean of a normal distribution.
We tackle two different cases:
when we know the variance of the distribution, then we use a z-statistic to conduct the test;
when the variance is unknown, then we use the t-statistic.
In each case we derive the power and the size of the test.
We conclude with two solved exercises on size and power.
Table of contents
Known variance: the z-test
The null hypothesis, the test statistic, the critical region, the decision, the power function, the size of the test, how to choose the critical value, unknown variance: the t-test, how to choose the critical values, solved exercises.
The assumptions are the same we made in the lecture on confidence intervals for the mean .
A test of hypothesis based on it is called z-test .
Otherwise, it is not rejected.
![hypothesis testing for means [eq7]](https://www.statlect.com/images/hypothesis-testing-mean__19.png)
We explain how to do this in the page on critical values .
This case is similar to the previous one. The only difference is that we now relax the assumption that the variance of the distribution is known.
The test of hypothesis based on it is called t-test .
Otherwise, we do not reject it.
The page on critical values explains how this equation is solved.
Below you can find some exercises with explained solutions.
Suppose that a statistician observes 100 independent realizations of a normal random variable.
The mean and the variance of the random variable, which the statistician does not know, are equal to 1 and 4 respectively.
Find the probability that the statistician will reject the null hypothesis that the mean is equal to zero if:
she runs a t-test based on the 100 observed realizations;
A statistician observes 100 independent realizations of a normal random variable.
She performs a t-test of the null hypothesis that the mean of the variable is equal to zero.
![hypothesis testing for means [eq38]](https://www.statlect.com/images/hypothesis-testing-mean__116.png)
How to cite
Please cite as:
Taboga, Marco (2021). "Hypothesis tests about the mean", Lectures on probability theory and mathematical statistics. Kindle Direct Publishing. Online appendix. https://www.statlect.com/fundamentals-of-statistics/hypothesis-testing-mean.
Most of the learning materials found on this website are now available in a traditional textbook format.
- Gamma function
- Characteristic function
- Uniform distribution
- Mean square convergence
- Convergence in probability
- Likelihood ratio test
- Statistical inference
- Point estimation
- Combinations
- Mathematical tools
- Fundamentals of probability
- Probability distributions
- Asymptotic theory
- Fundamentals of statistics
- About Statlect
- Cookies, privacy and terms of use
- Discrete random variable
- Mean squared error
- Continuous mapping theorem
- Alternative hypothesis
- Probability density function
- IID sequence
- To enhance your privacy,
- we removed the social buttons,
- but don't forget to share .
Teach yourself statistics
Hypothesis Test: Difference Between Means
This lesson explains how to conduct a hypothesis test for the difference between two means. The test procedure, called the two-sample t-test , is appropriate when the following conditions are met:
- The sampling method for each sample is simple random sampling .
- The samples are independent .
- Each population is at least 20 times larger than its respective sample .
- The population distribution is normal.
- The population data are symmetric , unimodal , without outliers , and the sample size is 15 or less.
- The population data are slightly skewed , unimodal, without outliers, and the sample size is 16 to 40.
- The sample size is greater than 40, without outliers.
This approach consists of four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results.
State the Hypotheses
Every hypothesis test requires the analyst to state a null hypothesis and an alternative hypothesis . The hypotheses are stated in such a way that they are mutually exclusive. That is, if one is true, the other must be false; and vice versa.
The table below shows three sets of null and alternative hypotheses. Each makes a statement about the difference d between the mean of one population μ 1 and the mean of another population μ 2 . (In the table, the symbol ≠ means " not equal to ".)
| Set | Null hypothesis | Alternative hypothesis | Number of tails |
|---|---|---|---|
| 1 | μ - μ = d | μ - μ ≠ d | 2 |
| 2 | μ - μ d | μ - μ < d | 1 |
| 3 | μ - μ d | μ - μ > d | 1 |
The first set of hypotheses (Set 1) is an example of a two-tailed test , since an extreme value on either side of the sampling distribution would cause a researcher to reject the null hypothesis. The other two sets of hypotheses (Sets 2 and 3) are one-tailed tests , since an extreme value on only one side of the sampling distribution would cause a researcher to reject the null hypothesis.
When the null hypothesis states that there is no difference between the two population means (i.e., d = 0), the null and alternative hypothesis are often stated in the following form.
H o : μ 1 = μ 2
H a : μ 1 ≠ μ 2
Formulate an Analysis Plan
The analysis plan describes how to use sample data to accept or reject the null hypothesis. It should specify the following elements.
- Significance level. Often, researchers choose significance levels equal to 0.01, 0.05, or 0.10; but any value between 0 and 1 can be used.
- Test method. Use the two-sample t-test to determine whether the difference between means found in the sample is significantly different from the hypothesized difference between means.
Analyze Sample Data
Using sample data, find the standard error, degrees of freedom, test statistic, and the P-value associated with the test statistic.
SE = sqrt[ (s 1 2 /n 1 ) + (s 2 2 /n 2 ) ]
DF = (s 1 2 /n 1 + s 2 2 /n 2 ) 2 / { [ (s 1 2 / n 1 ) 2 / (n 1 - 1) ] + [ (s 2 2 / n 2 ) 2 / (n 2 - 1) ] }
t = [ ( x 1 - x 2 ) - d ] / SE
- P-value. The P-value is the probability of observing a sample statistic as extreme as the test statistic. Since the test statistic is a t statistic, use the t Distribution Calculator to assess the probability associated with the t statistic, having the degrees of freedom computed above. (See sample problems at the end of this lesson for examples of how this is done.)
Interpret Results
If the sample findings are unlikely, given the null hypothesis, the researcher rejects the null hypothesis. Typically, this involves comparing the P-value to the significance level , and rejecting the null hypothesis when the P-value is less than the significance level.
Test Your Understanding
In this section, two sample problems illustrate how to conduct a hypothesis test of a difference between mean scores. The first problem involves a two-tailed test; the second problem, a one-tailed test.
Problem 1: Two-Tailed Test
Within a school district, students were randomly assigned to one of two Math teachers - Mrs. Smith and Mrs. Jones. After the assignment, Mrs. Smith had 30 students, and Mrs. Jones had 25 students.
At the end of the year, each class took the same standardized test. Mrs. Smith's students had an average test score of 78, with a standard deviation of 10; and Mrs. Jones' students had an average test score of 85, with a standard deviation of 15.
Test the hypothesis that Mrs. Smith and Mrs. Jones are equally effective teachers. Use a 0.10 level of significance. (Assume that student performance is approximately normal.)
Solution: The solution to this problem takes four steps: (1) state the hypotheses, (2) formulate an analysis plan, (3) analyze sample data, and (4) interpret results. We work through those steps below:
State the hypotheses. The first step is to state the null hypothesis and an alternative hypothesis.
Null hypothesis: μ 1 - μ 2 = 0
Alternative hypothesis: μ 1 - μ 2 ≠ 0
- Formulate an analysis plan . For this analysis, the significance level is 0.10. Using sample data, we will conduct a two-sample t-test of the null hypothesis.
SE = sqrt[(s 1 2 /n 1 ) + (s 2 2 /n 2 )]
SE = sqrt[(10 2 /30) + (15 2 /25] = sqrt(3.33 + 9)
SE = sqrt(12.33) = 3.51
DF = (10 2 /30 + 15 2 /25) 2 / { [ (10 2 / 30) 2 / (29) ] + [ (15 2 / 25) 2 / (24) ] }
DF = (3.33 + 9) 2 / { [ (3.33) 2 / (29) ] + [ (9) 2 / (24) ] } = 152.03 / (0.382 + 3.375) = 152.03/3.757 = 40.47
t = [ ( x 1 - x 2 ) - d ] / SE = [ (78 - 85) - 0 ] / 3.51 = -7/3.51 = -1.99
where s 1 is the standard deviation of sample 1, s 2 is the standard deviation of sample 2, n 1 is the size of sample 1, n 2 is the size of sample 2, x 1 is the mean of sample 1, x 2 is the mean of sample 2, d is the hypothesized difference between the population means, and SE is the standard error.
Since we have a two-tailed test , the P-value is the probability that a t statistic having 40 degrees of freedom is more extreme than -1.99; that is, less than -1.99 or greater than 1.99.
We use the t Distribution Calculator to find P(t < -1.99) is about 0.027.
- If you enter 1.99 as the sample mean in the t Distribution Calculator, you will find the that the P(t ≤ 1.99) is about 0.973. Therefore, P(t > 1.99) is 1 minus 0.973 or 0.027. Thus, the P-value = 0.027 + 0.027 = 0.054.
- Interpret results . Since the P-value (0.054) is less than the significance level (0.10), we cannot accept the null hypothesis.
Note: If you use this approach on an exam, you may also want to mention why this approach is appropriate. Specifically, the approach is appropriate because the sampling method was simple random sampling, the samples were independent, the sample size was much smaller than the population size, and the samples were drawn from a normal population.
Problem 2: One-Tailed Test
The Acme Company has developed a new battery. The engineer in charge claims that the new battery will operate continuously for at least 7 minutes longer than the old battery.
To test the claim, the company selects a simple random sample of 100 new batteries and 100 old batteries. The old batteries run continuously for 190 minutes with a standard deviation of 20 minutes; the new batteries, 200 minutes with a standard deviation of 40 minutes.
Test the engineer's claim that the new batteries run at least 7 minutes longer than the old. Use a 0.05 level of significance. (Assume that there are no outliers in either sample.)
Null hypothesis: μ 1 - μ 2 <= 7
Alternative hypothesis: μ 1 - μ 2 > 7
where μ 1 is battery life for the new battery, and μ 2 is battery life for the old battery.
- Formulate an analysis plan . For this analysis, the significance level is 0.05. Using sample data, we will conduct a two-sample t-test of the null hypothesis.
SE = sqrt[(40 2 /100) + (20 2 /100]
SE = sqrt(16 + 4) = 4.472
DF = (40 2 /100 + 20 2 /100) 2 / { [ (40 2 / 100) 2 / (99) ] + [ (20 2 / 100) 2 / (99) ] }
DF = (20) 2 / { [ (16) 2 / (99) ] + [ (2) 2 / (99) ] } = 400 / (2.586 + 0.162) = 145.56
t = [ ( x 1 - x 2 ) - d ] / SE = [(200 - 190) - 7] / 4.472 = 3/4.472 = 0.67
where s 1 is the standard deviation of sample 1, s 2 is the standard deviation of sample 2, n 1 is the size of sample 1, n 2 is the size of sample 2, x 1 is the mean of sample 1, x 2 is the mean of sample 2, d is the hypothesized difference between population means, and SE is the standard error.
Here is the logic of the analysis: Given the alternative hypothesis (μ 1 - μ 2 > 7), we want to know whether the observed difference in sample means is big enough (i.e., sufficiently greater than 7) to cause us to reject the null hypothesis.
Interpret results . Suppose we replicated this study many times with different samples. If the true difference in population means were actually 7, we would expect the observed difference in sample means to be 10 or less in 75% of our samples. And we would expect to find an observed difference to be more than 10 in 25% of our samples Therefore, the P-value in this analysis is 0.25.
- Skip to secondary menu
- Skip to main content
- Skip to primary sidebar
Statistics By Jim
Making statistics intuitive
Hypothesis Testing: Uses, Steps & Example
By Jim Frost 4 Comments
What is Hypothesis Testing?
Hypothesis testing in statistics uses sample data to infer the properties of a whole population . These tests determine whether a random sample provides sufficient evidence to conclude an effect or relationship exists in the population. Researchers use them to help separate genuine population-level effects from false effects that random chance can create in samples. These methods are also known as significance testing.

For example, researchers are testing a new medication to see if it lowers blood pressure. They compare a group taking the drug to a control group taking a placebo. If their hypothesis test results are statistically significant, the medication’s effect of lowering blood pressure likely exists in the broader population, not just the sample studied.
Using Hypothesis Tests
A hypothesis test evaluates two mutually exclusive statements about a population to determine which statement the sample data best supports. These two statements are called the null hypothesis and the alternative hypothesis . The following are typical examples:
- Null Hypothesis : The effect does not exist in the population.
- Alternative Hypothesis : The effect does exist in the population.
Hypothesis testing accounts for the inherent uncertainty of using a sample to draw conclusions about a population, which reduces the chances of false discoveries. These procedures determine whether the sample data are sufficiently inconsistent with the null hypothesis that you can reject it. If you can reject the null, your data favor the alternative statement that an effect exists in the population.
Statistical significance in hypothesis testing indicates that an effect you see in sample data also likely exists in the population after accounting for random sampling error , variability, and sample size. Your results are statistically significant when the p-value is less than your significance level or, equivalently, when your confidence interval excludes the null hypothesis value.
Conversely, non-significant results indicate that despite an apparent sample effect, you can’t be sure it exists in the population. It could be chance variation in the sample and not a genuine effect.
Learn more about Failing to Reject the Null .
5 Steps of Significance Testing
Hypothesis testing involves five key steps, each critical to validating a research hypothesis using statistical methods:
- Formulate the Hypotheses : Write your research hypotheses as a null hypothesis (H 0 ) and an alternative hypothesis (H A ).
- Data Collection : Gather data specifically aimed at testing the hypothesis.
- Conduct A Test : Use a suitable statistical test to analyze your data.
- Make a Decision : Based on the statistical test results, decide whether to reject the null hypothesis or fail to reject it.
- Report the Results : Summarize and present the outcomes in your report’s results and discussion sections.
While the specifics of these steps can vary depending on the research context and the data type, the fundamental process of hypothesis testing remains consistent across different studies.
Let’s work through these steps in an example!
Hypothesis Testing Example
Researchers want to determine if a new educational program improves student performance on standardized tests. They randomly assign 30 students to a control group , which follows the standard curriculum, and another 30 students to a treatment group, which participates in the new educational program. After a semester, they compare the test scores of both groups.
Download the CSV data file to perform the hypothesis testing yourself: Hypothesis_Testing .
The researchers write their hypotheses. These statements apply to the population, so they use the mu (μ) symbol for the population mean parameter .
- Null Hypothesis (H 0 ) : The population means of the test scores for the two groups are equal (μ 1 = μ 2 ).
- Alternative Hypothesis (H A ) : The population means of the test scores for the two groups are unequal (μ 1 ≠ μ 2 ).
Choosing the correct hypothesis test depends on attributes such as data type and number of groups. Because they’re using continuous data and comparing two means, the researchers use a 2-sample t-test .
Here are the results.

The treatment group’s mean is 58.70, compared to the control group’s mean of 48.12. The mean difference is 10.67 points. Use the test’s p-value and significance level to determine whether this difference is likely a product of random fluctuation in the sample or a genuine population effect.
Because the p-value (0.000) is less than the standard significance level of 0.05, the results are statistically significant, and we can reject the null hypothesis. The sample data provides sufficient evidence to conclude that the new program’s effect exists in the population.
Limitations
Hypothesis testing improves your effectiveness in making data-driven decisions. However, it is not 100% accurate because random samples occasionally produce fluky results. Hypothesis tests have two types of errors, both relating to drawing incorrect conclusions.
- Type I error: The test rejects a true null hypothesis—a false positive.
- Type II error: The test fails to reject a false null hypothesis—a false negative.
Learn more about Type I and Type II Errors .
Our exploration of hypothesis testing using a practical example of an educational program reveals its powerful ability to guide decisions based on statistical evidence. Whether you’re a student, researcher, or professional, understanding and applying these procedures can open new doors to discovering insights and making informed decisions. Let this tool empower your analytical endeavors as you navigate through the vast seas of data.
Learn more about the Hypothesis Tests for Various Data Types .
Share this:

Reader Interactions
June 10, 2024 at 10:51 am
Thank you, Jim, for another helpful article; timely too since I have started reading your new book on hypothesis testing and, now that we are at the end of the school year, my district is asking me to perform a number of evaluations on instructional programs. This is where my question/concern comes in. You mention that hypothesis testing is all about testing samples. However, I use all the students in my district when I make these comparisons. Since I am using the entire “population” in my evaluations (I don’t select a sample of third grade students, for example, but I use all 700 third graders), am I somehow misusing the tests? Or can I rest assured that my district’s student population is only a sample of the universal population of students?
June 10, 2024 at 1:50 pm
I hope you are finding the book helpful!
Yes, the purpose of hypothesis testing is to infer the properties of a population while accounting for random sampling error.
In your case, it comes down to how you want to use the results. Who do you want the results to apply to?
If you’re summarizing the sample, looking for trends and patterns, or evaluating those students and don’t plan to apply those results to other students, you don’t need hypothesis testing because there is no sampling error. They are the population and you can just use descriptive statistics. In this case, you’d only need to focus on the practical significance of the effect sizes.
On the other hand, if you want to apply the results from this group to other students, you’ll need hypothesis testing. However, there is the complicating issue of what population your sample of students represent. I’m sure your district has its own unique characteristics, demographics, etc. Your district’s students probably don’t adequately represent a universal population. At the very least, you’d need to recognize any special attributes of your district and how they could bias the results when trying to apply them outside the district. Or they might apply to similar districts in your region.
However, I’d imagine your 3rd graders probably adequately represent future classes of 3rd graders in your district. You need to be alert to changing demographics. At least in the short run I’d imagine they’d be representative of future classes.
Think about how these results will be used. Do they just apply to the students you measured? Then you don’t need hypothesis tests. However, if the results are being used to infer things about other students outside of the sample, you’ll need hypothesis testing along with considering how well your students represent the other students and how they differ.
I hope that helps!
June 10, 2024 at 3:21 pm
Thank you so much, Jim, for the suggestions in terms of what I need to think about and consider! You are always so clear in your explanations!!!!
June 10, 2024 at 3:22 pm
You’re very welcome! Best of luck with your evaluations!
Comments and Questions Cancel reply
Hypothesis Testing
Hypothesis testing is a tool for making statistical inferences about the population data. It is an analysis tool that tests assumptions and determines how likely something is within a given standard of accuracy. Hypothesis testing provides a way to verify whether the results of an experiment are valid.
A null hypothesis and an alternative hypothesis are set up before performing the hypothesis testing. This helps to arrive at a conclusion regarding the sample obtained from the population. In this article, we will learn more about hypothesis testing, its types, steps to perform the testing, and associated examples.
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. | |
| 7. | |
| 8. |
What is Hypothesis Testing in Statistics?
Hypothesis testing uses sample data from the population to draw useful conclusions regarding the population probability distribution . It tests an assumption made about the data using different types of hypothesis testing methodologies. The hypothesis testing results in either rejecting or not rejecting the null hypothesis.
Hypothesis Testing Definition
Hypothesis testing can be defined as a statistical tool that is used to identify if the results of an experiment are meaningful or not. It involves setting up a null hypothesis and an alternative hypothesis. These two hypotheses will always be mutually exclusive. This means that if the null hypothesis is true then the alternative hypothesis is false and vice versa. An example of hypothesis testing is setting up a test to check if a new medicine works on a disease in a more efficient manner.
Null Hypothesis
The null hypothesis is a concise mathematical statement that is used to indicate that there is no difference between two possibilities. In other words, there is no difference between certain characteristics of data. This hypothesis assumes that the outcomes of an experiment are based on chance alone. It is denoted as \(H_{0}\). Hypothesis testing is used to conclude if the null hypothesis can be rejected or not. Suppose an experiment is conducted to check if girls are shorter than boys at the age of 5. The null hypothesis will say that they are the same height.
Alternative Hypothesis
The alternative hypothesis is an alternative to the null hypothesis. It is used to show that the observations of an experiment are due to some real effect. It indicates that there is a statistical significance between two possible outcomes and can be denoted as \(H_{1}\) or \(H_{a}\). For the above-mentioned example, the alternative hypothesis would be that girls are shorter than boys at the age of 5.
Hypothesis Testing P Value
In hypothesis testing, the p value is used to indicate whether the results obtained after conducting a test are statistically significant or not. It also indicates the probability of making an error in rejecting or not rejecting the null hypothesis.This value is always a number between 0 and 1. The p value is compared to an alpha level, \(\alpha\) or significance level. The alpha level can be defined as the acceptable risk of incorrectly rejecting the null hypothesis. The alpha level is usually chosen between 1% to 5%.
Hypothesis Testing Critical region
All sets of values that lead to rejecting the null hypothesis lie in the critical region. Furthermore, the value that separates the critical region from the non-critical region is known as the critical value.
Hypothesis Testing Formula
Depending upon the type of data available and the size, different types of hypothesis testing are used to determine whether the null hypothesis can be rejected or not. The hypothesis testing formula for some important test statistics are given below:
- z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\). \(\overline{x}\) is the sample mean, \(\mu\) is the population mean, \(\sigma\) is the population standard deviation and n is the size of the sample.
- t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\). s is the sample standard deviation.
- \(\chi ^{2} = \sum \frac{(O_{i}-E_{i})^{2}}{E_{i}}\). \(O_{i}\) is the observed value and \(E_{i}\) is the expected value.
We will learn more about these test statistics in the upcoming section.
Types of Hypothesis Testing
Selecting the correct test for performing hypothesis testing can be confusing. These tests are used to determine a test statistic on the basis of which the null hypothesis can either be rejected or not rejected. Some of the important tests used for hypothesis testing are given below.
Hypothesis Testing Z Test
A z test is a way of hypothesis testing that is used for a large sample size (n ≥ 30). It is used to determine whether there is a difference between the population mean and the sample mean when the population standard deviation is known. It can also be used to compare the mean of two samples. It is used to compute the z test statistic. The formulas are given as follows:
- One sample: z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).
- Two samples: z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).
Hypothesis Testing t Test
The t test is another method of hypothesis testing that is used for a small sample size (n < 30). It is also used to compare the sample mean and population mean. However, the population standard deviation is not known. Instead, the sample standard deviation is known. The mean of two samples can also be compared using the t test.
- One sample: t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\).
- Two samples: t = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{s_{1}^{2}}{n_{1}}+\frac{s_{2}^{2}}{n_{2}}}}\).
Hypothesis Testing Chi Square
The Chi square test is a hypothesis testing method that is used to check whether the variables in a population are independent or not. It is used when the test statistic is chi-squared distributed.
One Tailed Hypothesis Testing
One tailed hypothesis testing is done when the rejection region is only in one direction. It can also be known as directional hypothesis testing because the effects can be tested in one direction only. This type of testing is further classified into the right tailed test and left tailed test.
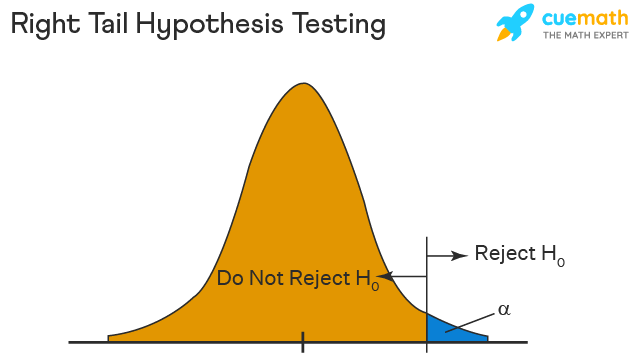
Right Tailed Hypothesis Testing
The right tail test is also known as the upper tail test. This test is used to check whether the population parameter is greater than some value. The null and alternative hypotheses for this test are given as follows:
\(H_{0}\): The population parameter is ≤ some value
\(H_{1}\): The population parameter is > some value.
If the test statistic has a greater value than the critical value then the null hypothesis is rejected
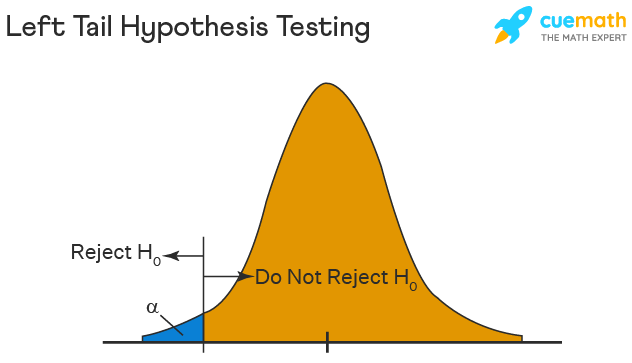
Left Tailed Hypothesis Testing
The left tail test is also known as the lower tail test. It is used to check whether the population parameter is less than some value. The hypotheses for this hypothesis testing can be written as follows:
\(H_{0}\): The population parameter is ≥ some value
\(H_{1}\): The population parameter is < some value.
The null hypothesis is rejected if the test statistic has a value lesser than the critical value.
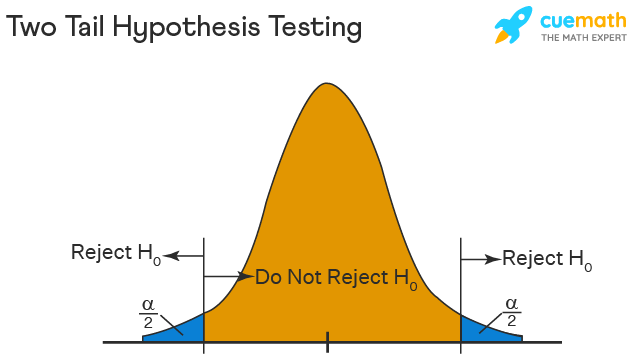
Two Tailed Hypothesis Testing
In this hypothesis testing method, the critical region lies on both sides of the sampling distribution. It is also known as a non - directional hypothesis testing method. The two-tailed test is used when it needs to be determined if the population parameter is assumed to be different than some value. The hypotheses can be set up as follows:
\(H_{0}\): the population parameter = some value
\(H_{1}\): the population parameter ≠ some value
The null hypothesis is rejected if the test statistic has a value that is not equal to the critical value.
Hypothesis Testing Steps
Hypothesis testing can be easily performed in five simple steps. The most important step is to correctly set up the hypotheses and identify the right method for hypothesis testing. The basic steps to perform hypothesis testing are as follows:
- Step 1: Set up the null hypothesis by correctly identifying whether it is the left-tailed, right-tailed, or two-tailed hypothesis testing.
- Step 2: Set up the alternative hypothesis.
- Step 3: Choose the correct significance level, \(\alpha\), and find the critical value.
- Step 4: Calculate the correct test statistic (z, t or \(\chi\)) and p-value.
- Step 5: Compare the test statistic with the critical value or compare the p-value with \(\alpha\) to arrive at a conclusion. In other words, decide if the null hypothesis is to be rejected or not.
Hypothesis Testing Example
The best way to solve a problem on hypothesis testing is by applying the 5 steps mentioned in the previous section. Suppose a researcher claims that the mean average weight of men is greater than 100kgs with a standard deviation of 15kgs. 30 men are chosen with an average weight of 112.5 Kgs. Using hypothesis testing, check if there is enough evidence to support the researcher's claim. The confidence interval is given as 95%.
Step 1: This is an example of a right-tailed test. Set up the null hypothesis as \(H_{0}\): \(\mu\) = 100.
Step 2: The alternative hypothesis is given by \(H_{1}\): \(\mu\) > 100.
Step 3: As this is a one-tailed test, \(\alpha\) = 100% - 95% = 5%. This can be used to determine the critical value.
1 - \(\alpha\) = 1 - 0.05 = 0.95
0.95 gives the required area under the curve. Now using a normal distribution table, the area 0.95 is at z = 1.645. A similar process can be followed for a t-test. The only additional requirement is to calculate the degrees of freedom given by n - 1.
Step 4: Calculate the z test statistic. This is because the sample size is 30. Furthermore, the sample and population means are known along with the standard deviation.
z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\).
\(\mu\) = 100, \(\overline{x}\) = 112.5, n = 30, \(\sigma\) = 15
z = \(\frac{112.5-100}{\frac{15}{\sqrt{30}}}\) = 4.56
Step 5: Conclusion. As 4.56 > 1.645 thus, the null hypothesis can be rejected.
Hypothesis Testing and Confidence Intervals
Confidence intervals form an important part of hypothesis testing. This is because the alpha level can be determined from a given confidence interval. Suppose a confidence interval is given as 95%. Subtract the confidence interval from 100%. This gives 100 - 95 = 5% or 0.05. This is the alpha value of a one-tailed hypothesis testing. To obtain the alpha value for a two-tailed hypothesis testing, divide this value by 2. This gives 0.05 / 2 = 0.025.
Related Articles:
- Probability and Statistics
- Data Handling
Important Notes on Hypothesis Testing
- Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant.
- It involves the setting up of a null hypothesis and an alternate hypothesis.
- There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
- Hypothesis testing can be classified as right tail, left tail, and two tail tests.
Examples on Hypothesis Testing
- Example 1: The average weight of a dumbbell in a gym is 90lbs. However, a physical trainer believes that the average weight might be higher. A random sample of 5 dumbbells with an average weight of 110lbs and a standard deviation of 18lbs. Using hypothesis testing check if the physical trainer's claim can be supported for a 95% confidence level. Solution: As the sample size is lesser than 30, the t-test is used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) > 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 5, s = 18. \(\alpha\) = 0.05 Using the t-distribution table, the critical value is 2.132 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = 2.484 As 2.484 > 2.132, the null hypothesis is rejected. Answer: The average weight of the dumbbells may be greater than 90lbs
- Example 2: The average score on a test is 80 with a standard deviation of 10. With a new teaching curriculum introduced it is believed that this score will change. On random testing, the score of 38 students, the mean was found to be 88. With a 0.05 significance level, is there any evidence to support this claim? Solution: This is an example of two-tail hypothesis testing. The z test will be used. \(H_{0}\): \(\mu\) = 80, \(H_{1}\): \(\mu\) ≠ 80 \(\overline{x}\) = 88, \(\mu\) = 80, n = 36, \(\sigma\) = 10. \(\alpha\) = 0.05 / 2 = 0.025 The critical value using the normal distribution table is 1.96 z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) z = \(\frac{88-80}{\frac{10}{\sqrt{36}}}\) = 4.8 As 4.8 > 1.96, the null hypothesis is rejected. Answer: There is a difference in the scores after the new curriculum was introduced.
- Example 3: The average score of a class is 90. However, a teacher believes that the average score might be lower. The scores of 6 students were randomly measured. The mean was 82 with a standard deviation of 18. With a 0.05 significance level use hypothesis testing to check if this claim is true. Solution: The t test will be used. \(H_{0}\): \(\mu\) = 90, \(H_{1}\): \(\mu\) < 90 \(\overline{x}\) = 110, \(\mu\) = 90, n = 6, s = 18 The critical value from the t table is -2.015 t = \(\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}\) t = \(\frac{82-90}{\frac{18}{\sqrt{6}}}\) t = -1.088 As -1.088 > -2.015, we fail to reject the null hypothesis. Answer: There is not enough evidence to support the claim.
go to slide go to slide go to slide

Book a Free Trial Class
FAQs on Hypothesis Testing
What is hypothesis testing.
Hypothesis testing in statistics is a tool that is used to make inferences about the population data. It is also used to check if the results of an experiment are valid.
What is the z Test in Hypothesis Testing?
The z test in hypothesis testing is used to find the z test statistic for normally distributed data . The z test is used when the standard deviation of the population is known and the sample size is greater than or equal to 30.
What is the t Test in Hypothesis Testing?
The t test in hypothesis testing is used when the data follows a student t distribution . It is used when the sample size is less than 30 and standard deviation of the population is not known.

What is the formula for z test in Hypothesis Testing?
The formula for a one sample z test in hypothesis testing is z = \(\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}\) and for two samples is z = \(\frac{(\overline{x_{1}}-\overline{x_{2}})-(\mu_{1}-\mu_{2})}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}}+\frac{\sigma_{2}^{2}}{n_{2}}}}\).
What is the p Value in Hypothesis Testing?
The p value helps to determine if the test results are statistically significant or not. In hypothesis testing, the null hypothesis can either be rejected or not rejected based on the comparison between the p value and the alpha level.
What is One Tail Hypothesis Testing?
When the rejection region is only on one side of the distribution curve then it is known as one tail hypothesis testing. The right tail test and the left tail test are two types of directional hypothesis testing.
What is the Alpha Level in Two Tail Hypothesis Testing?
To get the alpha level in a two tail hypothesis testing divide \(\alpha\) by 2. This is done as there are two rejection regions in the curve.
Tutorial Playlist
Statistics tutorial, everything you need to know about the probability density function in statistics, the best guide to understand central limit theorem, an in-depth guide to measures of central tendency : mean, median and mode, the ultimate guide to understand conditional probability.
A Comprehensive Look at Percentile in Statistics
The Best Guide to Understand Bayes Theorem
Everything you need to know about the normal distribution, an in-depth explanation of cumulative distribution function, a complete guide to chi-square test, what is hypothesis testing in statistics types and examples, understanding the fundamentals of arithmetic and geometric progression, the definitive guide to understand spearman’s rank correlation, mean squared error: overview, examples, concepts and more, all you need to know about the empirical rule in statistics, the complete guide to skewness and kurtosis, a holistic look at bernoulli distribution.
All You Need to Know About Bias in Statistics
A Complete Guide to Get a Grasp of Time Series Analysis
The Key Differences Between Z-Test Vs. T-Test
The Complete Guide to Understand Pearson's Correlation
A complete guide on the types of statistical studies, everything you need to know about poisson distribution, your best guide to understand correlation vs. regression, the most comprehensive guide for beginners on what is correlation, hypothesis testing in statistics - types | examples.
Lesson 10 of 24 By Avijeet Biswal

Table of Contents
In today’s data-driven world, decisions are based on data all the time. Hypothesis plays a crucial role in that process, whether it may be making business decisions, in the health sector, academia, or in quality improvement. Without hypothesis & hypothesis tests, you risk drawing the wrong conclusions and making bad decisions. In this tutorial, you will look at Hypothesis Testing in Statistics.
The Ultimate Ticket to Top Data Science Job Roles
What Is Hypothesis Testing in Statistics?
Hypothesis Testing is a type of statistical analysis in which you put your assumptions about a population parameter to the test. It is used to estimate the relationship between 2 statistical variables.
Let's discuss few examples of statistical hypothesis from real-life -
- A teacher assumes that 60% of his college's students come from lower-middle-class families.
- A doctor believes that 3D (Diet, Dose, and Discipline) is 90% effective for diabetic patients.
Now that you know about hypothesis testing, look at the two types of hypothesis testing in statistics.
Hypothesis Testing Formula
Z = ( x̅ – μ0 ) / (σ /√n)
- Here, x̅ is the sample mean,
- μ0 is the population mean,
- σ is the standard deviation,
- n is the sample size.
How Hypothesis Testing Works?
An analyst performs hypothesis testing on a statistical sample to present evidence of the plausibility of the null hypothesis. Measurements and analyses are conducted on a random sample of the population to test a theory. Analysts use a random population sample to test two hypotheses: the null and alternative hypotheses.
The null hypothesis is typically an equality hypothesis between population parameters; for example, a null hypothesis may claim that the population means return equals zero. The alternate hypothesis is essentially the inverse of the null hypothesis (e.g., the population means the return is not equal to zero). As a result, they are mutually exclusive, and only one can be correct. One of the two possibilities, however, will always be correct.
Your Dream Career is Just Around The Corner!
Null Hypothesis and Alternative Hypothesis
The Null Hypothesis is the assumption that the event will not occur. A null hypothesis has no bearing on the study's outcome unless it is rejected.
H0 is the symbol for it, and it is pronounced H-naught.
The Alternate Hypothesis is the logical opposite of the null hypothesis. The acceptance of the alternative hypothesis follows the rejection of the null hypothesis. H1 is the symbol for it.
Let's understand this with an example.
A sanitizer manufacturer claims that its product kills 95 percent of germs on average.
To put this company's claim to the test, create a null and alternate hypothesis.
H0 (Null Hypothesis): Average = 95%.
Alternative Hypothesis (H1): The average is less than 95%.
Another straightforward example to understand this concept is determining whether or not a coin is fair and balanced. The null hypothesis states that the probability of a show of heads is equal to the likelihood of a show of tails. In contrast, the alternate theory states that the probability of a show of heads and tails would be very different.
Become a Data Scientist with Hands-on Training!
Hypothesis Testing Calculation With Examples
Let's consider a hypothesis test for the average height of women in the United States. Suppose our null hypothesis is that the average height is 5'4". We gather a sample of 100 women and determine that their average height is 5'5". The standard deviation of population is 2.
To calculate the z-score, we would use the following formula:
z = ( x̅ – μ0 ) / (σ /√n)
z = (5'5" - 5'4") / (2" / √100)
z = 0.5 / (0.045)
We will reject the null hypothesis as the z-score of 11.11 is very large and conclude that there is evidence to suggest that the average height of women in the US is greater than 5'4".
Steps in Hypothesis Testing
Hypothesis testing is a statistical method to determine if there is enough evidence in a sample of data to infer that a certain condition is true for the entire population. Here’s a breakdown of the typical steps involved in hypothesis testing:
Formulate Hypotheses
- Null Hypothesis (H0): This hypothesis states that there is no effect or difference, and it is the hypothesis you attempt to reject with your test.
- Alternative Hypothesis (H1 or Ha): This hypothesis is what you might believe to be true or hope to prove true. It is usually considered the opposite of the null hypothesis.
Choose the Significance Level (α)
The significance level, often denoted by alpha (α), is the probability of rejecting the null hypothesis when it is true. Common choices for α are 0.05 (5%), 0.01 (1%), and 0.10 (10%).
Select the Appropriate Test
Choose a statistical test based on the type of data and the hypothesis. Common tests include t-tests, chi-square tests, ANOVA, and regression analysis. The selection depends on data type, distribution, sample size, and whether the hypothesis is one-tailed or two-tailed.
Collect Data
Gather the data that will be analyzed in the test. This data should be representative of the population to infer conclusions accurately.
Calculate the Test Statistic
Based on the collected data and the chosen test, calculate a test statistic that reflects how much the observed data deviates from the null hypothesis.
Determine the p-value
The p-value is the probability of observing test results at least as extreme as the results observed, assuming the null hypothesis is correct. It helps determine the strength of the evidence against the null hypothesis.
Make a Decision
Compare the p-value to the chosen significance level:
- If the p-value ≤ α: Reject the null hypothesis, suggesting sufficient evidence in the data supports the alternative hypothesis.
- If the p-value > α: Do not reject the null hypothesis, suggesting insufficient evidence to support the alternative hypothesis.
Report the Results
Present the findings from the hypothesis test, including the test statistic, p-value, and the conclusion about the hypotheses.
Perform Post-hoc Analysis (if necessary)
Depending on the results and the study design, further analysis may be needed to explore the data more deeply or to address multiple comparisons if several hypotheses were tested simultaneously.
Types of Hypothesis Testing
To determine whether a discovery or relationship is statistically significant, hypothesis testing uses a z-test. It usually checks to see if two means are the same (the null hypothesis). Only when the population standard deviation is known and the sample size is 30 data points or more, can a z-test be applied.
A statistical test called a t-test is employed to compare the means of two groups. To determine whether two groups differ or if a procedure or treatment affects the population of interest, it is frequently used in hypothesis testing.
Chi-Square
You utilize a Chi-square test for hypothesis testing concerning whether your data is as predicted. To determine if the expected and observed results are well-fitted, the Chi-square test analyzes the differences between categorical variables from a random sample. The test's fundamental premise is that the observed values in your data should be compared to the predicted values that would be present if the null hypothesis were true.
Hypothesis Testing and Confidence Intervals
Both confidence intervals and hypothesis tests are inferential techniques that depend on approximating the sample distribution. Data from a sample is used to estimate a population parameter using confidence intervals. Data from a sample is used in hypothesis testing to examine a given hypothesis. We must have a postulated parameter to conduct hypothesis testing.
Bootstrap distributions and randomization distributions are created using comparable simulation techniques. The observed sample statistic is the focal point of a bootstrap distribution, whereas the null hypothesis value is the focal point of a randomization distribution.
A variety of feasible population parameter estimates are included in confidence ranges. In this lesson, we created just two-tailed confidence intervals. There is a direct connection between these two-tail confidence intervals and these two-tail hypothesis tests. The results of a two-tailed hypothesis test and two-tailed confidence intervals typically provide the same results. In other words, a hypothesis test at the 0.05 level will virtually always fail to reject the null hypothesis if the 95% confidence interval contains the predicted value. A hypothesis test at the 0.05 level will nearly certainly reject the null hypothesis if the 95% confidence interval does not include the hypothesized parameter.
Become a Data Scientist through hands-on learning with hackathons, masterclasses, webinars, and Ask-Me-Anything! Start learning now!
Simple and Composite Hypothesis Testing
Depending on the population distribution, you can classify the statistical hypothesis into two types.
Simple Hypothesis: A simple hypothesis specifies an exact value for the parameter.
Composite Hypothesis: A composite hypothesis specifies a range of values.
A company is claiming that their average sales for this quarter are 1000 units. This is an example of a simple hypothesis.
Suppose the company claims that the sales are in the range of 900 to 1000 units. Then this is a case of a composite hypothesis.
One-Tailed and Two-Tailed Hypothesis Testing
The One-Tailed test, also called a directional test, considers a critical region of data that would result in the null hypothesis being rejected if the test sample falls into it, inevitably meaning the acceptance of the alternate hypothesis.
In a one-tailed test, the critical distribution area is one-sided, meaning the test sample is either greater or lesser than a specific value.
In two tails, the test sample is checked to be greater or less than a range of values in a Two-Tailed test, implying that the critical distribution area is two-sided.
If the sample falls within this range, the alternate hypothesis will be accepted, and the null hypothesis will be rejected.
Become a Data Scientist With Real-World Experience
Right Tailed Hypothesis Testing
If the larger than (>) sign appears in your hypothesis statement, you are using a right-tailed test, also known as an upper test. Or, to put it another way, the disparity is to the right. For instance, you can contrast the battery life before and after a change in production. Your hypothesis statements can be the following if you want to know if the battery life is longer than the original (let's say 90 hours):
- The null hypothesis is (H0 <= 90) or less change.
- A possibility is that battery life has risen (H1) > 90.
The crucial point in this situation is that the alternate hypothesis (H1), not the null hypothesis, decides whether you get a right-tailed test.
Left Tailed Hypothesis Testing
Alternative hypotheses that assert the true value of a parameter is lower than the null hypothesis are tested with a left-tailed test; they are indicated by the asterisk "<".
Suppose H0: mean = 50 and H1: mean not equal to 50
According to the H1, the mean can be greater than or less than 50. This is an example of a Two-tailed test.
In a similar manner, if H0: mean >=50, then H1: mean <50
Here the mean is less than 50. It is called a One-tailed test.
Type 1 and Type 2 Error
A hypothesis test can result in two types of errors.
Type 1 Error: A Type-I error occurs when sample results reject the null hypothesis despite being true.
Type 2 Error: A Type-II error occurs when the null hypothesis is not rejected when it is false, unlike a Type-I error.
Suppose a teacher evaluates the examination paper to decide whether a student passes or fails.
H0: Student has passed
H1: Student has failed
Type I error will be the teacher failing the student [rejects H0] although the student scored the passing marks [H0 was true].
Type II error will be the case where the teacher passes the student [do not reject H0] although the student did not score the passing marks [H1 is true].
Our Data Scientist Master's Program covers core topics such as R, Python, Machine Learning, Tableau, Hadoop, and Spark. Get started on your journey today!
Limitations of Hypothesis Testing
Hypothesis testing has some limitations that researchers should be aware of:
- It cannot prove or establish the truth: Hypothesis testing provides evidence to support or reject a hypothesis, but it cannot confirm the absolute truth of the research question.
- Results are sample-specific: Hypothesis testing is based on analyzing a sample from a population, and the conclusions drawn are specific to that particular sample.
- Possible errors: During hypothesis testing, there is a chance of committing type I error (rejecting a true null hypothesis) or type II error (failing to reject a false null hypothesis).
- Assumptions and requirements: Different tests have specific assumptions and requirements that must be met to accurately interpret results.
Learn All The Tricks Of The BI Trade
After reading this tutorial, you would have a much better understanding of hypothesis testing, one of the most important concepts in the field of Data Science . The majority of hypotheses are based on speculation about observed behavior, natural phenomena, or established theories.
If you are interested in statistics of data science and skills needed for such a career, you ought to explore the Post Graduate Program in Data Science.
If you have any questions regarding this ‘Hypothesis Testing In Statistics’ tutorial, do share them in the comment section. Our subject matter expert will respond to your queries. Happy learning!
1. What is hypothesis testing in statistics with example?
Hypothesis testing is a statistical method used to determine if there is enough evidence in a sample data to draw conclusions about a population. It involves formulating two competing hypotheses, the null hypothesis (H0) and the alternative hypothesis (Ha), and then collecting data to assess the evidence. An example: testing if a new drug improves patient recovery (Ha) compared to the standard treatment (H0) based on collected patient data.
2. What is H0 and H1 in statistics?
In statistics, H0 and H1 represent the null and alternative hypotheses. The null hypothesis, H0, is the default assumption that no effect or difference exists between groups or conditions. The alternative hypothesis, H1, is the competing claim suggesting an effect or a difference. Statistical tests determine whether to reject the null hypothesis in favor of the alternative hypothesis based on the data.
3. What is a simple hypothesis with an example?
A simple hypothesis is a specific statement predicting a single relationship between two variables. It posits a direct and uncomplicated outcome. For example, a simple hypothesis might state, "Increased sunlight exposure increases the growth rate of sunflowers." Here, the hypothesis suggests a direct relationship between the amount of sunlight (independent variable) and the growth rate of sunflowers (dependent variable), with no additional variables considered.
4. What are the 3 major types of hypothesis?
The three major types of hypotheses are:
- Null Hypothesis (H0): Represents the default assumption, stating that there is no significant effect or relationship in the data.
- Alternative Hypothesis (Ha): Contradicts the null hypothesis and proposes a specific effect or relationship that researchers want to investigate.
- Nondirectional Hypothesis: An alternative hypothesis that doesn't specify the direction of the effect, leaving it open for both positive and negative possibilities.
Find our PL-300 Microsoft Power BI Certification Training Online Classroom training classes in top cities:
| Name | Date | Place | |
|---|---|---|---|
| 7 Sep -22 Sep 2024, Weekend batch | Your City | ||
| 21 Sep -6 Oct 2024, Weekend batch | Your City | ||
| 12 Oct -27 Oct 2024, Weekend batch | Your City |
About the Author
Avijeet is a Senior Research Analyst at Simplilearn. Passionate about Data Analytics, Machine Learning, and Deep Learning, Avijeet is also interested in politics, cricket, and football.
Recommended Resources
Free eBook: Top Programming Languages For A Data Scientist
Normality Test in Minitab: Minitab with Statistics
Machine Learning Career Guide: A Playbook to Becoming a Machine Learning Engineer
- PMP, PMI, PMBOK, CAPM, PgMP, PfMP, ACP, PBA, RMP, SP, and OPM3 are registered marks of the Project Management Institute, Inc.
- Search Search Please fill out this field.
What Is Hypothesis Testing?
- How It Works
4 Step Process
The bottom line.
- Fundamental Analysis
Hypothesis Testing: 4 Steps and Example
:max_bytes(150000):strip_icc():format(webp)/ChristinaMajaski-5c9433ea46e0fb0001d880b1.jpeg)
Hypothesis testing, sometimes called significance testing, is an act in statistics whereby an analyst tests an assumption regarding a population parameter. The methodology employed by the analyst depends on the nature of the data used and the reason for the analysis.
Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data. Such data may come from a larger population or a data-generating process. The word "population" will be used for both of these cases in the following descriptions.
Key Takeaways
- Hypothesis testing is used to assess the plausibility of a hypothesis by using sample data.
- The test provides evidence concerning the plausibility of the hypothesis, given the data.
- Statistical analysts test a hypothesis by measuring and examining a random sample of the population being analyzed.
- The four steps of hypothesis testing include stating the hypotheses, formulating an analysis plan, analyzing the sample data, and analyzing the result.
How Hypothesis Testing Works
In hypothesis testing, an analyst tests a statistical sample, intending to provide evidence on the plausibility of the null hypothesis. Statistical analysts measure and examine a random sample of the population being analyzed. All analysts use a random population sample to test two different hypotheses: the null hypothesis and the alternative hypothesis.
The null hypothesis is usually a hypothesis of equality between population parameters; e.g., a null hypothesis may state that the population mean return is equal to zero. The alternative hypothesis is effectively the opposite of a null hypothesis. Thus, they are mutually exclusive , and only one can be true. However, one of the two hypotheses will always be true.
The null hypothesis is a statement about a population parameter, such as the population mean, that is assumed to be true.
- State the hypotheses.
- Formulate an analysis plan, which outlines how the data will be evaluated.
- Carry out the plan and analyze the sample data.
- Analyze the results and either reject the null hypothesis, or state that the null hypothesis is plausible, given the data.
Example of Hypothesis Testing
If an individual wants to test that a penny has exactly a 50% chance of landing on heads, the null hypothesis would be that 50% is correct, and the alternative hypothesis would be that 50% is not correct. Mathematically, the null hypothesis is represented as Ho: P = 0.5. The alternative hypothesis is shown as "Ha" and is identical to the null hypothesis, except with the equal sign struck-through, meaning that it does not equal 50%.
A random sample of 100 coin flips is taken, and the null hypothesis is tested. If it is found that the 100 coin flips were distributed as 40 heads and 60 tails, the analyst would assume that a penny does not have a 50% chance of landing on heads and would reject the null hypothesis and accept the alternative hypothesis.
If there were 48 heads and 52 tails, then it is plausible that the coin could be fair and still produce such a result. In cases such as this where the null hypothesis is "accepted," the analyst states that the difference between the expected results (50 heads and 50 tails) and the observed results (48 heads and 52 tails) is "explainable by chance alone."
When Did Hypothesis Testing Begin?
Some statisticians attribute the first hypothesis tests to satirical writer John Arbuthnot in 1710, who studied male and female births in England after observing that in nearly every year, male births exceeded female births by a slight proportion. Arbuthnot calculated that the probability of this happening by chance was small, and therefore it was due to “divine providence.”
What are the Benefits of Hypothesis Testing?
Hypothesis testing helps assess the accuracy of new ideas or theories by testing them against data. This allows researchers to determine whether the evidence supports their hypothesis, helping to avoid false claims and conclusions. Hypothesis testing also provides a framework for decision-making based on data rather than personal opinions or biases. By relying on statistical analysis, hypothesis testing helps to reduce the effects of chance and confounding variables, providing a robust framework for making informed conclusions.
What are the Limitations of Hypothesis Testing?
Hypothesis testing relies exclusively on data and doesn’t provide a comprehensive understanding of the subject being studied. Additionally, the accuracy of the results depends on the quality of the available data and the statistical methods used. Inaccurate data or inappropriate hypothesis formulation may lead to incorrect conclusions or failed tests. Hypothesis testing can also lead to errors, such as analysts either accepting or rejecting a null hypothesis when they shouldn’t have. These errors may result in false conclusions or missed opportunities to identify significant patterns or relationships in the data.
Hypothesis testing refers to a statistical process that helps researchers determine the reliability of a study. By using a well-formulated hypothesis and set of statistical tests, individuals or businesses can make inferences about the population that they are studying and draw conclusions based on the data presented. All hypothesis testing methods have the same four-step process, which includes stating the hypotheses, formulating an analysis plan, analyzing the sample data, and analyzing the result.
Sage. " Introduction to Hypothesis Testing ," Page 4.
Elder Research. " Who Invented the Null Hypothesis? "
Formplus. " Hypothesis Testing: Definition, Uses, Limitations and Examples ."
:max_bytes(150000):strip_icc():format(webp)/null_hypothesis-finalE-56a4132b022f49f0a3d469c6882ddd99.jpg)
- Terms of Service
- Editorial Policy
- Privacy Policy

IMAGES
COMMENTS
We then determine the appropriate test statistic (Step 2) for the hypothesis test. The formula for the test statistic is given below. Test Statistic for Testing H0: p = p 0. if min (np 0 , n (1-p 0 )) > 5. The formula above is appropriate for large samples, defined when the smaller of np 0 and n (1-p 0) is at least 5.
Table 8.3: One-sided hypothesis testing for the mean: H0: μ ≤ μ0, H1: μ > μ0. Note that the tests mentioned in Table 8.3 remain valid if we replace the null hypothesis by μ = μ0. The reason for this is that in choosing the threshold c, we assumed the worst case scenario, i.e, μ = μ0 .
Step 1: Determine the hypotheses. The hypotheses for a difference in two population means are similar to those for a difference in two population proportions. The null hypothesis, H 0, is again a statement of "no effect" or "no difference.". H 0: μ 1 - μ 2 = 0, which is the same as H 0: μ 1 = μ 2. The alternative hypothesis, H a ...
The mean pregnancy length is 266 days. We test the following hypotheses. H 0: μ = 266. H a: μ < 266. Suppose a random sample of 40 women who smoke during their pregnancy have a mean pregnancy length of 260 days with a standard deviation of 21 days. The P-value is 0.04.
Step 5: Present your findings. The results of hypothesis testing will be presented in the results and discussion sections of your research paper, dissertation or thesis.. In the results section you should give a brief summary of the data and a summary of the results of your statistical test (for example, the estimated difference between group means and associated p-value).
Full Hypothesis Test Examples. Example 8.2.4. Jeffrey, as an eight-year old, established a mean time of 16.43 seconds for swimming the 25-yard freestyle, with a standard deviation of 0.8 seconds. His dad, Frank, thought that Jeffrey could swim the 25-yard freestyle faster using goggles.
Hypothesis testing is a crucial procedure to perform when you want to make inferences about a population using a random sample. These inferences include estimating population properties such as the mean, differences between means, proportions, and the relationships between variables. This post provides an overview of statistical hypothesis testing.
Note that this does not mean that a sample mean of 192.1 indicates that the null hypothesis is true; it just doesn't provide compelling evidence to reject it. In essence, hypothesis testing is a procedure to compute a probability that reflects the strength of the evidence (based on a given sample) for rejecting the null hypothesis.
Outline 1 Homework Review 2 Introduction 3 Hypothesis Testing for the Mean The Hypotheses The Level of Significance The Test Statistic The Value of the Test Statistic The p-Value The Decision The Conclusion 4 Another Example 5 The TI-83 6 Assignment Robb T. Koether (Hampden-Sydney College) Hypothesis Testing for Means Mon, Mar 22, 2010 2 / 50
This lecture explains how to conduct hypothesis tests about the mean of a normal distribution. We tackle two different cases: when we know the variance of the distribution, then we use a z-statistic to conduct the test; when the variance is unknown, then we use the t-statistic. In each case we derive the power and the size of the test.
The first step is to state the null hypothesis and an alternative hypothesis. Null hypothesis: μ 1 - μ 2 = 0. Alternative hypothesis: μ 1 - μ 2 ≠ 0. Note that these hypotheses constitute a two-tailed test. The null hypothesis will be rejected if the difference between sample means is too big or if it is too small.
The researchers write their hypotheses. These statements apply to the population, so they use the mu (μ) symbol for the population mean parameter.. Null Hypothesis (H 0): The population means of the test scores for the two groups are equal (μ 1 = μ 2).; Alternative Hypothesis (H A): The population means of the test scores for the two groups are unequal (μ 1 ≠ μ 2).
A statistical hypothesis is an assumption about a population parameter.. For example, we may assume that the mean height of a male in the U.S. is 70 inches. The assumption about the height is the statistical hypothesis and the true mean height of a male in the U.S. is the population parameter.. A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical ...
Testing Hypotheses using Confidence Intervals. We can start the evaluation of the hypothesis setup by comparing 2006 and 2012 run times using a point estimate from the 2012 sample: x¯12 = 95.61 x ¯ 12 = 95.61 minutes. This estimate suggests the average time is actually longer than the 2006 time, 93.29 minutes.
A statistical hypothesis test is a method of statistical inference used to decide whether the data sufficiently supports a particular hypothesis. ... Hypothesis testing can mean any mixture of two formulations that both changed with time. Any discussion of significance testing vs hypothesis testing is doubly vulnerable to confusion.
An Independent Samples t-test compares the means for two groups. A Paired sample t-test compares means from the same group at different times (say, one year apart). A One sample t-test tests the mean of a single group against a known mean; Chi-Square Test. Chi-Square test is generally used when testing is related to categorical variables.
Answer. Set up the hypothesis test: A 5% level of significance means that α = 0.05 α = 0.05. This is a test of a single population mean. H0: μ = 65 Ha: μ > 65 H 0: μ = 65 H a: μ > 65. Since the instructor thinks the average score is higher, use a " > > ". The " > > " means the test is right-tailed.
Hypothesis testing is a technique that is used to verify whether the results of an experiment are statistically significant. It involves the setting up of a null hypothesis and an alternate hypothesis. There are three types of tests that can be conducted under hypothesis testing - z test, t test, and chi square test.
Components of a Formal Hypothesis Test. The null hypothesis is a statement about the value of a population parameter, such as the population mean (µ) or the population proportion (p).It contains the condition of equality and is denoted as H 0 (H-naught).. H 0: µ = 157 or H0 : p = 0.37. The alternative hypothesis is the claim to be tested, the opposite of the null hypothesis.
Hypothesis Testing Formula. Z = ( x̅ - μ0 ) / (σ /√n) Here, x̅ is the sample mean, μ0 is the population mean, σ is the standard deviation, n is the sample size. How Hypothesis Testing Works? An analyst performs hypothesis testing on a statistical sample to present evidence of the plausibility of the null hypothesis.
In hypothesis testing, the goal is to see if there is sufficient statistical evidence to reject a presumed null hypothesis in favor of a conjectured alternative hypothesis.The null hypothesis is usually denoted \(H_0\) while the alternative hypothesis is usually denoted \(H_1\). An hypothesis test is a statistical decision; the conclusion will either be to reject the null hypothesis in favor ...
Hypothesis testing is an act in statistics whereby an analyst tests an assumption regarding a population parameter. The methodology employed by the analyst depends on the nature of the data used ...
Hypothesis Testing Step 1: State the Hypotheses. In all three examples, our aim is to decide between two opposing points of view, Claim 1 and Claim 2. In hypothesis testing, Claim 1 is called the null hypothesis (denoted " Ho "), and Claim 2 plays the role of the alternative hypothesis (denoted " Ha ").