You're reading a free article with opinions that may differ from The Motley Fool's Premium Investing Services. Become a Motley Fool member today to get instant access to our top analyst recommendations, in-depth research, investing resources, and more. Learn More

The Smartest Bank Stocks to Buy With $500 Right Now
- Many bank stocks offer big dividends with impressive long-term track records.
- There are two stocks in particular that investors should be paying attention to right now.
- One of these picks may surprise you by being on this list.
- Motley Fool Issues Rare “All In” Buy Alert
NYSE: BRK.B
Berkshire hathaway.

If you're looking to invest in bank stocks, here are two great options to consider this month.
Bank stocks are an appealing option for many investors because they tend to offer appealing dividends as well as solid long-term returns. I say "tend to offer" because not all bank stocks are created equal nor do all bank stocks perform well.
If you're looking for the best bank stock ideas right now, the two picks featured below have real potential. And the second pick might just surprise you.
1. TD Bank: This stock has a proven history of profitability
When it comes to making money with bank stocks , Toronto-Dominion Bank ( TD 0.79% ) is a prime case study. Over the last 30 years, shares of TD Bank (as it is more commonly known) have posted an incredible total return (including dividends reinvested) of 3,140%. The S&P 500 's total return was 1,340% over the same time period.
What made TD Bank's rise so spectacular? It's partially due to the unique operating conditions of Canada's banking sector, where regulations encourage industry consolidation. For example, TD Bank is currently the second-largest bank in Canada, with $1.4 trillion in assets. The second-largest bank in the U.S. is Bank of America , which has assets of $3.3 billion despite the U.S. banking industry being many times larger than Canada's. Outsized market share has allowed TD Bank to post profits and returns on equity that its U.S. counterparts can't quite match. TD Bank's average annual return on equity over the past five years, for instance, has been roughly 13.2%. Bank of America, for comparison, has averaged just 9.7%.

TD Total Assets (Quarterly) data by YCharts
To be fair, TD Bank's performance in more recent years hasn't matched its historical average. Over the last three years, shares have delivered a total return of just 2% versus a total return for the S&P 500 of 30%. That underperformance is reflective of struggles in the banking sector as a whole. Bank of America shares, for instance, rose by just 0.8% over the same time period. It's also related to some U.S. regulatory issues from 2023 involving the bank's money-laundering controls that TD Bank is working to resolve. Until they are resolved, TD's growth could be somewhat slowed.
Investors could use this underperformance to their advantage. TD Bank currently trades at just 1.4 times book value, a discount versus its three-year average of 1.6 times book value. The dividend yield, too, recently hit new highs and now tops 5%. If you're looking for a bank stock with good value and a solid dividend that is well covered, TD Bank is for you.
2. Berkshire Hathaway: A secret way to bet on the best bank stocks
Berkshire Hathaway ( BRK.A 1.85% ) ( BRK.B 1.61% ) isn't a bank stock, but it owns stakes in enough bank stocks to qualify for consideration. For decades, CEO Warren Buffett has made Berkshire a big investor in a variety of banks. Right now, Berkshire's portfolio is betting tens of billions of dollars on well-known banks like Capital One , Citigroup , and Bank of America, as well as lesser-known banks like Ally Financial and Nu Holdings . In total, Berkshire's portfolio has more than $40 billion invested directly in bank stocks, with another $43 billion bet on financial services companies like Mastercard, American Express, and Visa . Berkshire is more of a bank stock than many realize.
Of course, buying Berkshire shares also exposes you to a wide variety of other businesses, and your direct exposure to banks will be relatively small. But the upside is that you get to outsource your bank stock picks to one of the best investors of all time: Warren Buffett . Buffett has outlined his strategy for investing in bank stocks before.
"It's a business that can be a very good business, when run right," he told investors in 1996. "There's no magic to it. You just have to stay away from doing something foolish." With Buffett managing your bank stock portfolio, you're much less likely to invest in a bank stock bust.
Despite the holding company recently topping $1 trillion in market cap for the first time, Berkshire Hathaway's valuation is highly reasonable, especially considering the quality of the conglomerate. Shares trade just shy of 1.7 times book value, a figure that is likely overstated due to massive share buybacks, which grow shareholder value but tend to depress accounting book value.
It's a strange pick as a bank stock, but Berkshire could be a great fit for those looking to add banking sector exposure while diversifying much of the risk.
Ally is an advertising partner of The Ascent, a Motley Fool company. Bank of America is an advertising partner of The Ascent, a Motley Fool company. Citigroup is an advertising partner of The Ascent, a Motley Fool company. American Express is an advertising partner of The Ascent, a Motley Fool company. Ryan Vanzo has no position in any of the stocks mentioned. The Motley Fool has positions in and recommends Bank of America, Berkshire Hathaway, Mastercard, and Visa. The Motley Fool recommends Nu Holdings and recommends the following options: long January 2025 $370 calls on Mastercard and short January 2025 $380 calls on Mastercard. The Motley Fool has a disclosure policy .
Related Articles

Premium Investing Services
Invest better with The Motley Fool. Get stock recommendations, portfolio guidance, and more from The Motley Fool's premium services.
Apple CEO Tim Cook is living out the Hollywood movie executive fantasy in Italy right now
- Tim Cook, the CEO of Apple, is living the high life in Italy.
- Cook and other Apple executives attended the Venice Film Festival in Italy.
- Here's a look at the glitz, glam, and luxury.

Apple CEO Tim Cook showed up in style at the 81st Venice International Film Festival in Italy this weekend, where he rubbed shoulders with some of Hollywood's elite.
He and other Apple executives are promoting "Disclaimer," an Apple TV+ limited series that will premiere at the festival and then debut worldwide in October.
Here is a look at what Cook and his colleagues were up to over the weekend.
Tim Cook walked the red carpet in Venice.
The day before Cook walked the red carpet on August 29, he joined George and Amal Clooney at their 18th-century villa on Lake Como, The Daily Mail reported.
The trio took a boat to dinner at Villa Passalacqua, a 5-star hotel.
Clooney and Brad Pitt are starring in "Wolfs," which is having its world premiere at the Venice Film Festival. After a limited theatrical release, it will be available on Apple TV+ on September 27.
During a press conference in Venice on Sunday, Clooney said it was "a bummer" that Apple was not giving the film a wider theatrical release.
Cook is promoting 'Disclaimer,' a limited series.
"Disclaimer," which stars Cate Blanchett and was written and directed by Alfonso Cuarón, is a "gripping psychological thriller" about a reporter who "built her reputation revealing the misdeeds and transgressions of others," an Apple press release said. The show will be released globally on October 11 on Apple TV+.
He enjoyed a luxury cocktail hour.
Cook spent the evening with Blanchett (who is also an executive producer on the series), Cuarón, and Eddy Cue, Apple's senior vice president of Services.
They enjoyed a cocktail hour at the hotel Excelsior Pool Bar, a luxury venue with a view.
And a celebration at a swanky hotel.
Cook, flanked by Apple executives and actors from the limited series, was also photographed at Palazzina Grassi, another 5-star luxury venue in Venice. The cost for a night at the hotel ranges from about $650 to $1,850.
- Main content

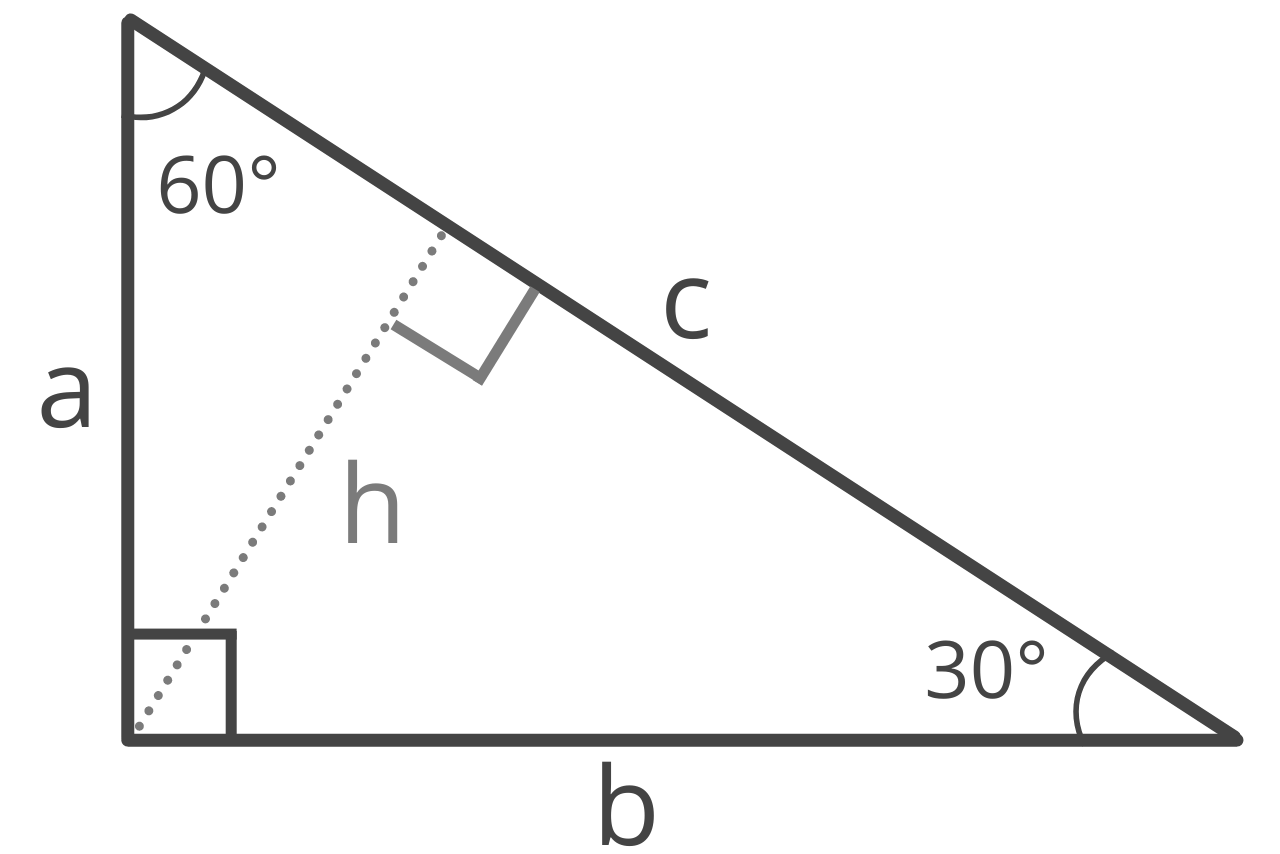
Right Triangles
Rules, Formula and more
Pythagorean Theorem
The sum of the squares of the lengths of the legs equals the square of the length of the hypotenuse .
Usually, this theorem is expressed as $$ A^2 + B^2 = C^2 $$ .
Right Triangle Properties

A right triangle has one $$ 90^{\circ} $$ angle ($$ \angle $$ B in the picture on the left) and a variety of often-studied formulas such as:
- The Pythagorean Theorem
- Trigonometry Ratios (SOHCAHTOA)
- Pythagorean Theorem vs Sohcahtoa (which to use)
SOHCAHTOA only applies to right triangles ( more here ) .
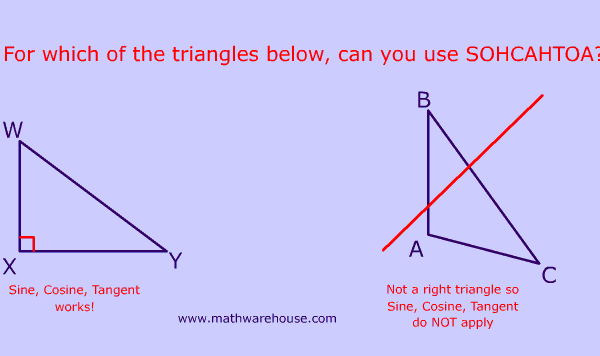
A Right Triangle's Hypotenuse
The hypotenuse is the largest side in a right triangle and is always opposite the right angle.

In the triangle above, the hypotenuse is the side AB which is opposite the right angle, $$ \angle C $$.
Online tool calculates the hypotenuse (or a leg) using the Pythagorean theorem.
Practice Problems
Below are several practice problems involving the Pythagorean theorem, you can also get more detailed lesson on how to use the Pythagorean theorem here .
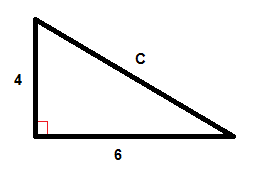
Find the length of side t in the triangle on the left.

Substitute the two known sides into the Pythagorean theorem's formula : A² + B² = C²
What is the value of x in the picture on the left?

Set up the Pythagorean Theorem : 14 2 + 48 2 = x 2 2,500 = X 2
$$ x = \sqrt{2500} = 50 $$

$$ x^2 = 21^2 + 72^2 \\ x^2= 5625 \\ x = \sqrt{5625} \\ x =75 $$
Find the length of side X in the triangle on on the left?
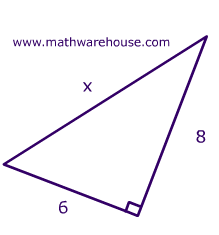
Substitue the two known sides into the pythagorean theorem's formula : $$ A^2 + B^2 = C^2 \\ 8^2 + 6^2 = x^2 \\ x = \sqrt{100}=10 $$
What is x in the triangle on the left?

x 2 + 4 2 = 5 2 x 2 + 16 = 25 x 2 = 25 - 16 = 9 x = 3
Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!
Popular pages @ mathwarehouse.com.


- Parallelogram
- Quadrilateral
- Parallelepiped
- Tetrahedron
- Dodecahedron
- Fraction Calculator
- Mixed Fraction Calculator
- Greatest Common Factor Calulator
- Decimal to Fraction Calculator
- Whole Numbers
- Rational Numbers
- Place Value
- Irrational Numbers
- Natural Numbers
- Binary Operation
- Numerator and Denominator
- Order of Operations (PEMDAS)
- Scientific Notation
Table of Contents
Last modified on August 3rd, 2023
#ezw_tco-2 .ez-toc-title{ font-size: 120%; ; ; } #ezw_tco-2 .ez-toc-widget-container ul.ez-toc-list li.active{ background-color: #ededed; } chapter outline
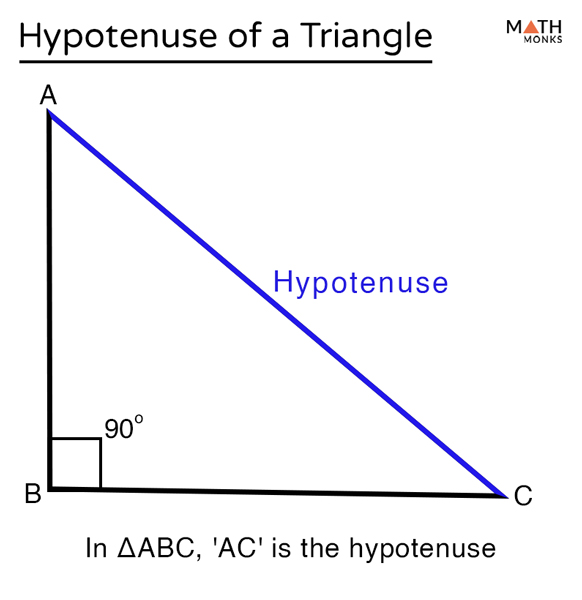
Hypotenuse of a triangle, what is the hypotenuse of a triangle.
A hypotenuse is the longest side of a right triangle. It is the side opposite the right angle (90°). The word ‘hypotenuse’ came from the Greek word ‘hypoteinousa’, meaning ‘stretching under’, where ‘hypo’ means ‘under’, and ‘teinein’ means ‘to stretch’.
How to Find the Hypotenuse of a Right Triangle
a) When Base and Height are Given
To calculate the hypotenuse of a right or right-angled triangle when its corresponding base and height are known, we use the given formula.
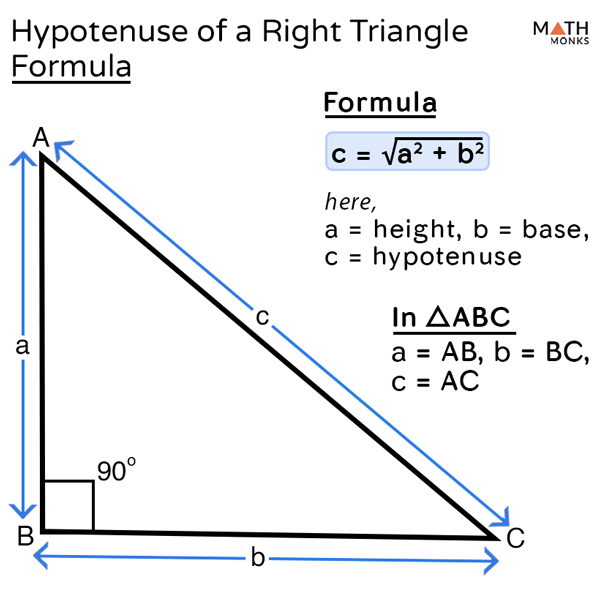
By Pythagorean Theorem,
(Hypotenuse) 2 = (Base) 2 + (Height) 2
Hypotenuse = √(Base) 2 + (Height) 2
Thus, mathematically, hypotenuse is the sum of the square of base and height of a right triangle.
The above formula is also written as,
c = √a 2 + b 2 , here c = hypotenuse, a = height, b = base
Let us solve some problems to understand the concept better.
Problem: Finding the hypotenuse of a right triangle, when the BASE and the HEIGHT are known.
What is the length of the hypotenuse of a right triangle with base 8m and height 6m.
As we know, c = √a 2 + b 2 , here a = 6m, b = 8m = √(6) 2 + (8) 2 = √36 + 64 = √100 = 10m
b) When Length of a Side and its Opposite Angle are Given
To find the hypotenuse of a right triangle when the length of a side and its opposite angle are known, we use the given formula, which is called the Law of sines.
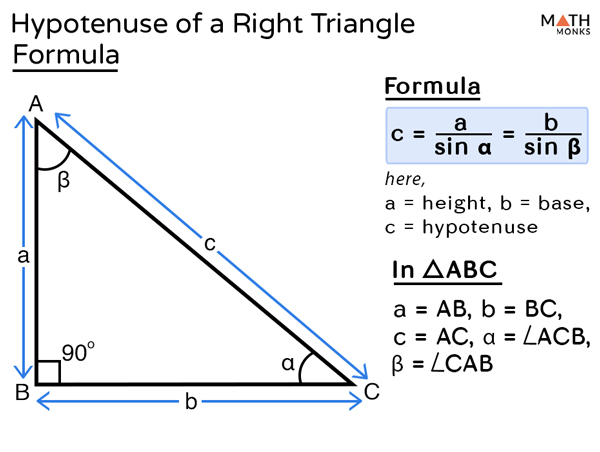
c = a/sin α = b/sin β, here c = hypotenuse, a = height, b = base, α = angle formed between hypotenuse and base, β = angle formed between hypotenuse and height
Problem: Finding the hypotenuse of a right triangle, when the LENGTH OF A SIDE and its OPPOSITE ANGLE is known.
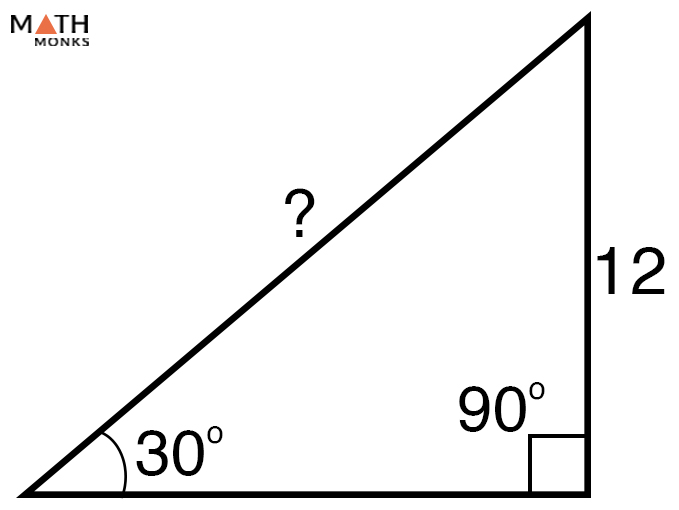
Here, we will use the Law of sines formula, c = a/sin α, here a = 12, α = 30° = 12/ sin 30° = 12 x 2 = 24 units
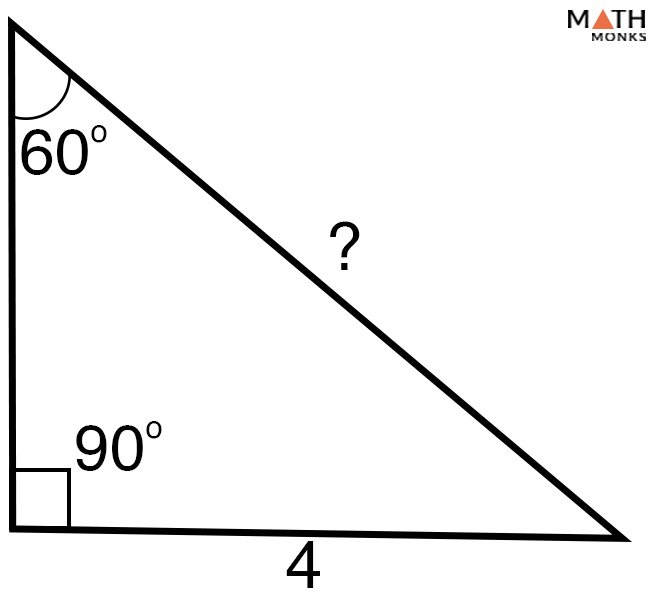
Using the Law of sines formula, c = b/sin β, b = 4, β = 60° = 4/ sin 60° = 8/√3 units
c) When the Area and Either Height or Base are Known
To determine the hypotenuse of a right triangle when the height or base is known, we use the Pythagorean Theorem to derive the formula as shown below:
As we know from the Pythagorean Theorem
c = √(a) 2 + (b) 2 …..(1), here c = hypotenuse, a = height, b = base
Area of right triangle (A) = a x b/2
b = area x 2/a …… (2)
a = area x 2/b …… (3)
Putting (2) in (1) we get,
c = √(a 2 + (area x 2/a) 2 )
Putting (3) in (1) we get,
c = √(b 2 + (area x 2/b) 2 )
Problem: Finding the hypotenuse of a right triangle, when the AREA and one SIDE are known.
What is the length of the hypotenuse of a right triangle with area 20m 2 and height 6m.
As we know, c = √(a 2 + (area x 2/a) 2 ), here area = 20m 2 , a = 6m = √6 2 + (20 x 2/6) 2 ) =√80.35 = 8.96 m
What is the length of the hypotenuse of a right triangle with area 14cm 2 and base 9cm.
As we know, c = √(b 2 + (area x 2/b) 2 ), here area = 14cm 2 , b = 9cm = √9 2 + (14 x 2/9) 2 ) = √45.67 = 6.75 m
How to Find the Hypotenuse of a Right Isosceles Triangle
To derive the formula for finding the hypotenuse of a right isosceles triangle we use the Pythagorean Theorem.
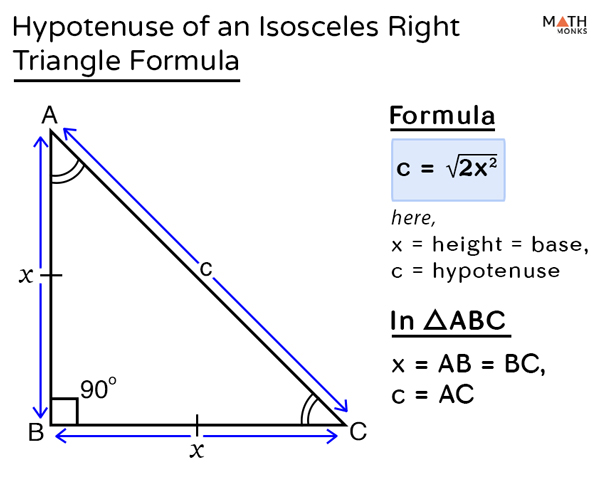
As we know,
c = √a 2 + b 2
Let the length of the two equal sides be x, such that (a = b = x)
c =√x 2 + x 2
What is the length of the hypotenuse of a right isosceles triangle with two equal sides measuring 5.5 cm each.
As we know, c = √2x, here x = 5.5 = √2 x 5.5 = 7.77 cm
Find the measure of the length of the hypotenuse of a 45-45-90 triangle with one of the two equal sides measuring 9 cm.
As a 45-45-90 triangle is a right isosceles triangle, we can apply the formula of right isosceles triangle for calculation of area As we know, c = √2x, here x = 9 cm =√2 x 9 = 12.72 cm
Leave a comment Cancel reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
- Privacy Policy
- Trigonometry
Join Our Newsletter
© 2024 Mathmonks.com . All rights reserved. Reproduction in whole or in part without permission is prohibited.
Hypotenuse Calculator
Calculate the length of the hypotenuse in a right triangle using two sides or one side and one angle with the calculator below.
- 1 Side & Adjacent Angle
- 1 Side & Opposite Angle
Have a Question or Feedback?
Hypotenuse:.
Chevron Down Icon scroll down
On this page:
How to find the hypotenuse of a right triangle, formula one: given two legs, formula two: given one leg and the adjacent angle, formula three: given one leg and the opposite angle, formula four: given one leg and the area, how to find the hypotenuse for a 45 45 90 right triangle, how to find the hypotenuse for a 30 60 90 right triangle.

Joe is the creator of Inch Calculator and has over 20 years of experience in engineering and construction. He holds several degrees and certifications.
Full bio Chevron Right Icon

Zach is a former math teacher with a Master's degree in education and a Bachelor's degree in mathematics, and is currently pursuing his PhD.
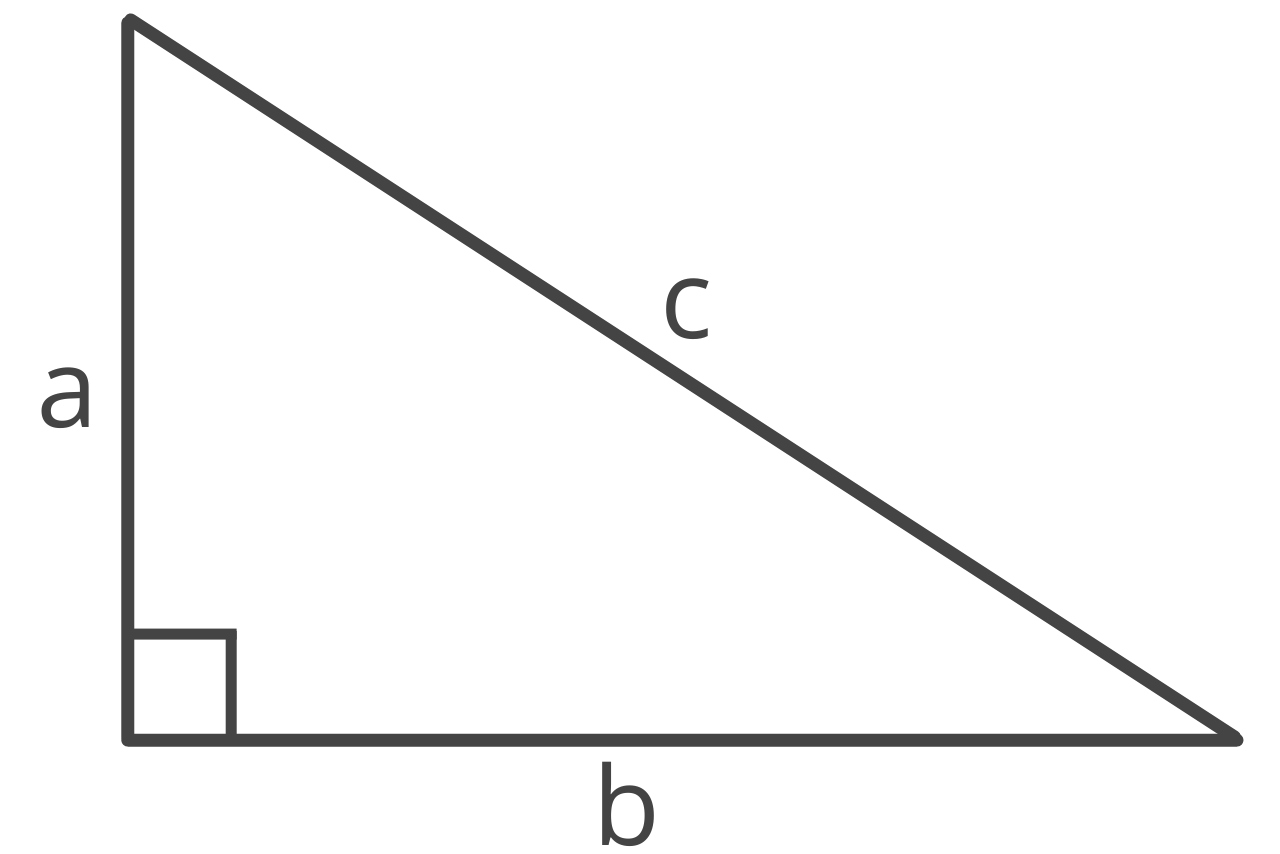
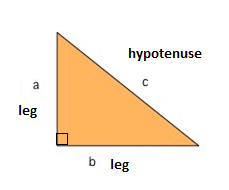
The hypotenuse is the longest side of a right triangle and is always opposite the 90° right angle.
The illustration below is a right triangle . The hypotenuse is labeled as c , and the opposite 90° angle is typically symbolized with the square drawn at the vertex.
The two shorter side lengths (often called the legs of a right triangle), are labeled as a & b , and are opposite the interior angles labeled α & β .
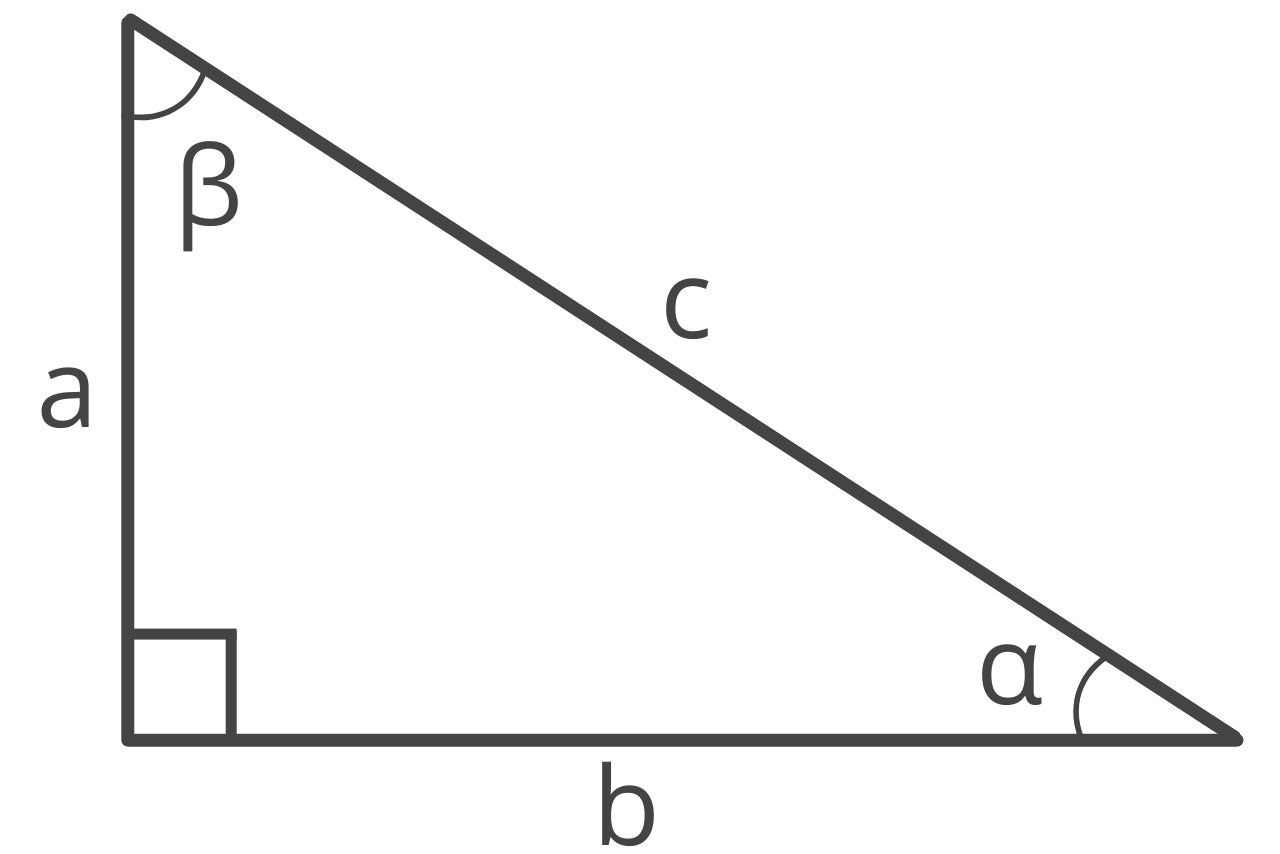
You can solve the hypotenuse using a little trigonometry and one of the following formulas.
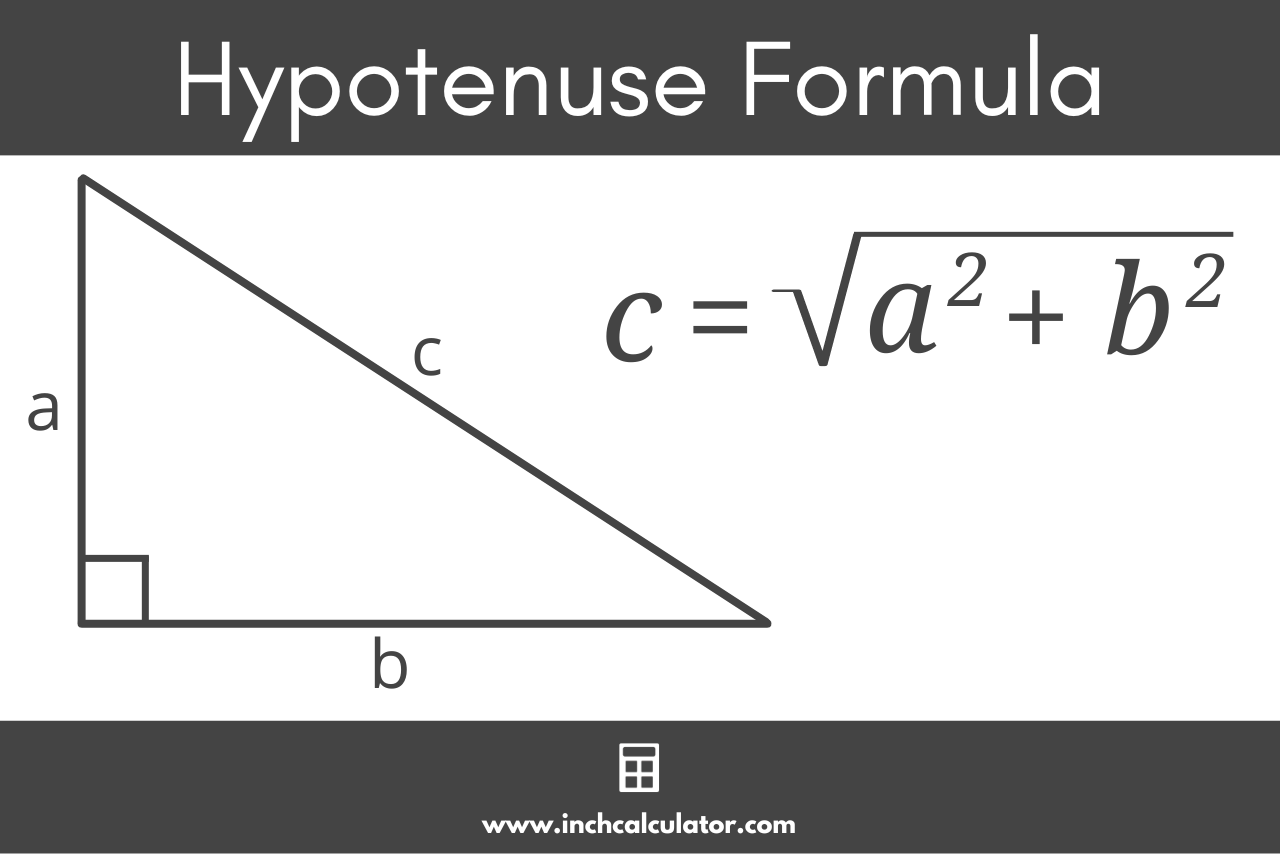
The Pythagorean theorem can be used to find the hypotenuse using the length of the two legs. The Pythagorean theorem states a² + b² = c² .
This formula can be rewritten to solve for the hypotenuse c :
c = a² + b²
Thus, the hypotenuse c is equal to the square root of the quantity leg a squared plus leg b squared.
Given the length of one leg and the adjacent angle, you can find the hypotenuse using the formula:
c = a / cos(β)
The hypotenuse c is equal to side a divided by the cosine of the adjacent angle β .
Given the length of one leg and the opposite angle, you can find the hypotenuse using the Law of Sines with the formula:
c = a / sin(α)
The hypotenuse c is equal to side a divided by the sine of the opposite angle α .
If you know the length of one of the legs and the triangle area , you can find the length of the hypotenuse by using the area formula to solve for the length of the other leg, then using the Pythagorean theorem.
Given the formula to find the area of a right triangle, start by finding the length of the other leg:
A = 1 / 2 ab
You can rearrange this formula to solve for the length of leg b like this:
The length of leg b is equal to 2 times the area A divided by the length of leg a .
Then, you can use the length of legs a and b to find the hypotenuse using the first formula above:
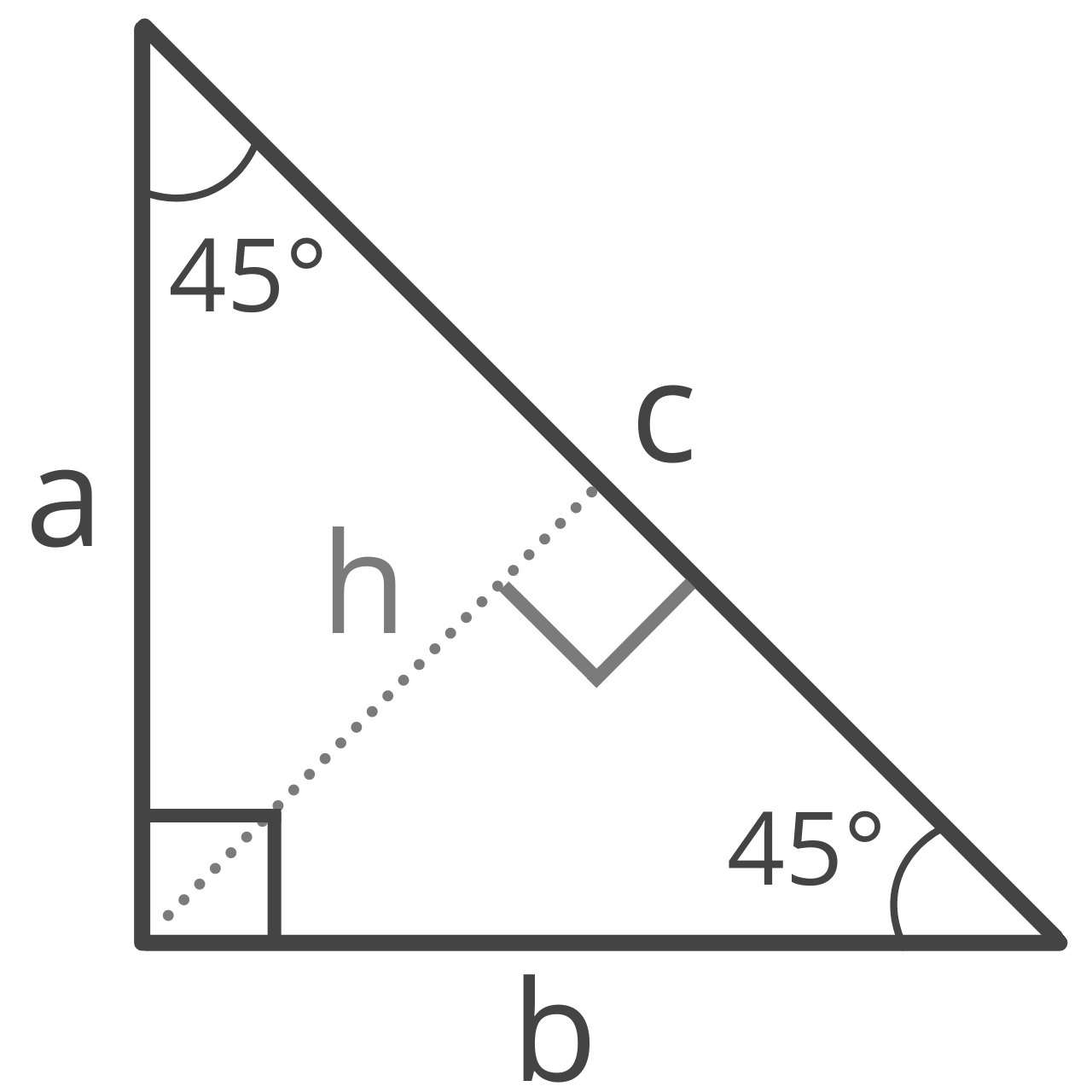
A 45 45 90 triangle is a special right triangle that is also an isosceles triangle. As the name implies, a 45 45 90 has two 45° interior angles and one right interior angle.
Since this is an isosceles triangle , both legs are equal in length, so you can find the length of the hypotenuse of a 45 45 90 right triangle using a simplified formula derived from the Pythagorean theorem.
c = a√2
The length of hypotenuse c is equal to the length of leg a times the square root of 2.
A 30 60 90 triangle is a special right triangle that has one 30° interior angle, one 60° interior angle, and one right interior angle.
In this special case, the length of the hypotenuse is always equal to two times the length of the shortest leg a of the triangle. Note, the shortest leg will always be opposite the 30° interior angle.
So, given the length of the shortest leg a , the formula to find the hypotenuse is:
The length of hypotenuse c is equal to 2 times the length of leg a .
Recommended Triangle Resources
- Triangle Area Calculator Right Arrow Icon
- Right Triangle Calculator Right Arrow Icon
- SOHCAHTOA Calculator Right Arrow Icon
- Triangle Calculator Right Arrow Icon
- Law of Cosines Calculator Right Arrow Icon
Hypotenuse, Adjacent And Opposite Sides Of A Right Triangle
Related Pages Right Triangles Basic Trigonometry Special Right Triangles Types Of Triangles More Geometry Lessons
In these lessons, we will learn the names of the sides of a right triangle (hypotenuse, adjacent, opposite) and how they are used in trigonometry.
Sides Of A Right Triangle
Hypotenuse, Adjacent and Opposite Sides .
In the following right triangle PQR,
- the side PQ, which is opposite to the right angle PRQ is called the hypotenuse . The hypotenuse is the longest side of the right triangle.
- the side RQ is called the adjacent side of angle θ.
- the side PR is called the opposite side of angle θ.
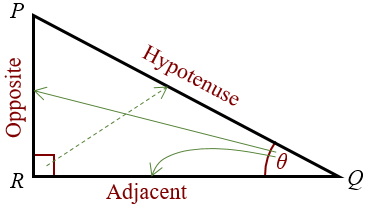
Note: The adjacent and the opposite sides depend on the angle θ. For complementary angle of θ, the labels of the 2 sides are reversed.
Example: Identify the hypotenuse, adjacent side and opposite side in the following triangle: a) for angle x b) for angle y
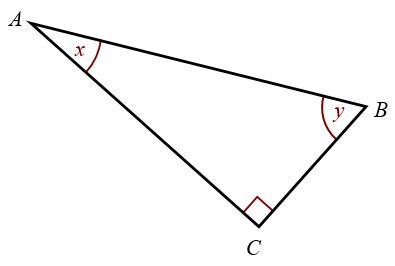
Solution: a) For angle x: AB is the hypotenuse, AC is the adjacent side , and BC is the opposite side. b) For angle y: AB is the hypotenuse, BC is the adjacent side , and AC is the opposite side.
SOH-CAH-TOA
The following diagram show how to use SOHCAHTOA for a right triangle.
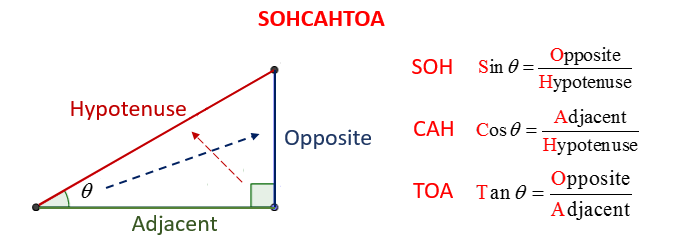
How to identify the Opposite Sides, Adjacent Sides and Hypotenuse of a Right Triangle?
Definition of Cos, Sin, Tan, Csc, Sec, Cot for the right triangle sin x = opposite/hypotenuse cos x = adjacent/hypotenuse tan x = opposite/adjacent csc x = 1/sin x = hypotenuse/opposite sec x = 1/cos x = hypotenuse/adjacent cot x = 1/tan x = adjacent/opposite
Using the Sine Formula (the SOH formula)
The first part of this video will explain the difference between the hypotenuse, adjacent and opposite sides of a right triangle. Then it shows how to use the sine formula (the SOH formula).
Sine = Opposite over the Hypotenuse
Using the Cosine Formula (the CAH formula)
Cosine = Adjacent over Hypotenuse
Using the Tangent Formula (the TOA formula)
Tangent = Opposite over Adjacent

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Hypotenuse of a Right Triangle – Formulas and Examples
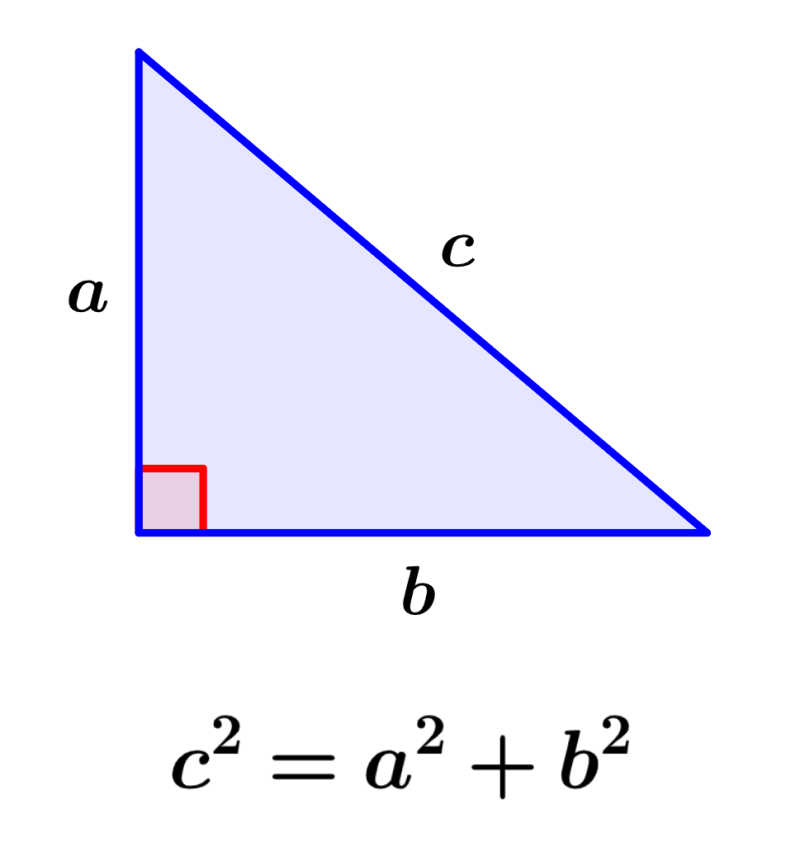
The hypotenuse of a right triangle is the side opposite the 90-degree angle. We can calculate the hypotenuse by using the Pythagorean theorem. This theorem tells us that the hypotenuse squared is equal to the sum of the squares of the lengths of the other two sides of the triangle. Therefore, to get the length of the hypotenuse, we need to have the lengths of the other sides.
Here, we will review the Pythagorean theorem. Also, we will use this theorem to solve some problems and find the length of the hypotenuse.
Relevant for …
Learning about the hypotenuse of a right triangle with examples.
See examples
How to find the hypotenuse of a right triangle?
Hypotenuse of a right triangle – examples with answers, hypotenuse of a right triangle – practice problems.
To find the hypotenuse of a right triangle, we use the Pythagorean theorem. Recall that the Pythagorean theorem tells us that the square of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. For example, let’s look at the following figure of a right triangle:
In this triangle, c is the hypotenuse since it is the side opposite the right angle. Therefore, the Pythagorean theorem tells us:
| $latex {{c}^2}={{a}^2}+{{b}^2}$ |
where c is the length of the hypotenuse, a and b are the lengths of the other two sides.
The Pythagorean theorem formula is used to solve the following examples. Each example has its respective solution, but it is recommended that you try to solve the exercises yourself to practice.
What is the length of the hypotenuse of a right triangle that has sides of length 3 m and 4 m?
We can recognize that we have sides $latex a=3$ and $latex b=4$. Therefore, we use the Pythagorean theorem with these values:
$latex {{c}^2}={{a}^2}+{{b}^2}$
$latex {{c}^2}={{3}^2}+{{4}^2}$
$latex {{c}^2}=9+16$
$latex {{c}^2}=25$
$latex c=5$
The length of the hypotenuse is 5 m.
We have a right triangle with sides of length 5 m and 12 m. What is its hypotenuse?
We have the side lengths $latex a=5$ and $latex b=12$. Therefore, we plug these values into the Pythagorean theorem:
$latex {{c}^2}={{5}^2}+{{12}^2}$
$latex {{c}^2}=25+144$
$latex {{c}^2}=169$
$latex c=13$
The length of the hypotenuse is 13 m.
What is the hypotenuse of a right triangle with sides of length 9 m and 12 m?
We have the lengths $latex a=9$ and $latex b=12$. Therefore, we plug these values into the Pythagorean theorem:
$latex {{c}^2}={{9}^2}+{{12}^2}$
$latex {{c}^2}=81+144$
$latex {{c}^2}=225$
$latex c=15$
The length of the hypotenuse is 15 m.
We have a right triangle with sides of length 10 m and 12 m. What is the length of its hypotenuse?
Here, we have the lengths $latex a=10$ and $latex b=12$. Therefore, we use these values in the Pythagorean theorem:
$latex {{c}^2}={{10}^2}+{{12}^2}$
$latex {{c}^2}=100+144$
$latex {{c}^2}=244$
$latex c=15.62$
The length of the hypotenuse is 15.62 m.
What is the length of the hypotenuse of a right triangle that has sides of length 20 cm and 10 cm?
We can recognize that we have sides $latex a=20$ and $latex b=10$. Therefore, we use the Pythagorean theorem with these values:
$latex {{c}^2}={{20}^2}+{{10}^2}$
$latex {{c}^2}=400+100$
$latex {{c}^2}=500$
$latex c=22.36$
The length of the hypotenuse is 22.36 cm.
Apply what you have learned about the Pythagorean Theorem to find the length of the hypotenuse of right triangles. If you need help with this, you can look at the solved examples above.
If we have a right triangle with sides of length 6m and 8m, what is its hypotenuse?
Choose an answer
A right triangle has sides of length 7m and 24m. What is the length of the hypotenuse?
If we have a right triangle with sides of length 11m and 15m, what is its hypotenuse, what is the length of the hypotenuse if the sides of the right triangle are 13cm and 17cm.
Interested in learning more about right triangles? Take a look at these pages:
- Area of a Right Triangle – Formulas and Examples
- Perimeter of a Right Triangle – Formulas and Examples
- What are the characteristics of right triangles?
- Isosceles Right Triangle – Formulas and Examples

Jefferson Huera Guzman
Jefferson is the lead author and administrator of Neurochispas.com. The interactive Mathematics and Physics content that I have created has helped many students.

Learn mathematics with our additional resources in different topics

Copyright © 2024 Neurochispas
All rights reserved.
INFORMATION
Terms and Conditions
Privacy Policy
About Neurochispas
About the Author
The longest side of a right triangle is called the hypotenuse. It lies opposite the right angle . The other two sides of a triangle go by a variety of names. Generally, they are referred to as the legs of the triangle, but they are also referred to as the opposite side or adjacent side and also the base or altitude of the triangle.
What is the hypotenuse
The hypotenuse is one of the sides in a right triangle that lies opposite the right angle of the triangle. It is the longest side of a right triangle. Note that the longest side of any triangle that is not a right triangle is not a hypotenuse. Only right triangles have a hypotenuse. The figure below shows a right triangle example and a hypotenuse example.
In this figure, the bottom leg may be referred to as the base while the left leg may be referred to as the altitude. Given the angle θ, the bottom leg would be referred to as the adjacent side while the left leg would be referred to as the opposite side.
It makes sense that the hypotenuse lies opposite the right angle of the triangle since the length of the sides of a triangle corresponds to the size of the angle opposite the side. Since the hypotenuse of a right triangle is the longest side of the triangle, the 90° angle opposite it is also the largest angle of the right triangle. This also makes sense because the internal angles of a triangle sum to 180°. Since all triangles have 3 sides and 3 internal angles, it is impossible for a right triangle to have another angle that is greater than or equal to 90°, because the third angle would have to be 0° or have a negative angle measurement.
How to find the hypotenuse
To find the hypotenuse of a triangle, there are a few different methods depending on the available information.
Hypotenuse formula
The hypotenuse formula refers to the Pythagorean Theorem when it is solved for the hypotenuse, c. The Pythagorean Theorem is a theorem specific to right triangles. It cannot be used with non-right triangles. For a right triangle with a hypotenuse of length c and leg lengths a and b, the Pythagorean Theorem states that:
Solving for c gives us the hypotenuse formula:
Below is a hypotenuse example using the Pythagorean Theorem.
Find the hypotenuse length of the triangle below.
Given legs a = 15 and b = 20:
c 2 = 15 2 + 20 2
So, the hypotenuse length is 25.
Using law of sines
To find the hypotenuse using the law of sines, reference the following figure and use the formula:
Thus, to find the hypotenuse using the law of sines, we need to know the measure of one angle and one leg. If we do, finding the hypotenuse is just a matter of plugging values into the formula.
Triangle trigonometric relationships
It is also possible to use triangle trigonometry with sine, cosine, and tangent to find the hypotenuse given a side and an angle of the triangle. Refer to the trigonometry section for more detail. Briefly, given the following right triangle
the following relationships can be used to find the various sides and angles of a right triangle:
In the relationships above, A, B, and C are the angles of the triangle opposite the sides a, b, and c, respectively.
Using area and one leg
To find the hypotenuse using the area and one leg, use the formula:
where b is the base of the triangle.
The hypotenuse is the largest side of a right triangle. It is a side opposite to the right angle in a right triangle. The Pythagoras theorem defines the relationship between the hypotenuse and the other two sides of the right triangle, the base, and the perpendicular side. The square of the hypotenuse is equal to the sum of the squares of the base and the perpendicular side of the right triangle.
The Pythagoras theorem has given the Pythagorean triplets and the largest value in Pythagorean triplets is the hypotenuse. Let us learn more about the hypotenuse in this article.
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. |
What is a Hypotenuse?
The hypotenuse is the longest side of a right-angled triangle . It is represented by the side opposite to the right angle. It is related to the other sides of the right triangle by the Pythagoras theorem . The square of the measure of the hypotenuse is equal to the sum of the squares of the other two sides of the right triangle. The hypotenuse can be easily recognized in a right triangle as the largest side.
Hypotenuse Definition: In a right-angled triangle, the longest side or the side opposite to the right angle is termed hypotenuse . The hypotenuse is related to the base and the altitude of the triangle , by the formula: Hypotenuse 2 = Base 2 + Altitude 2 . Let us look at the below real-world examples of a hypotenuse in right triangle-shaped objects.

Hypotenuse Equation
To derive an equation or a formula of the hypotenuse , years ago there was an interesting fact revealed about triangles. Hypotenuse equation : The fact states that with a right-angled triangle or a triangle with a 90º angle, squares can be framed using each of the three sides of the triangle. After putting squares against each side, it was observed that the biggest square has the exact same area as the other two squares. To simplify the whole observation, it was later put in a short equation that can also be called a hypotenuse equation.
So, the hypotenuse equation = a 2 + b 2 = c 2 , where c is the length of the hypotenuse and a and b are the other two sides of the right-angled triangle.
Now, look at the image given below to understand the derivation of the above formula. Here we have a = Perpendicular, b = Base, c = Hypotenuse.

Tips and Tricks on Hypotenuse:
The following points will help you to get a better understanding of the hypotenuse and its relation to the other two sides of the right triangle.
- The Pythagoras theorem states that in a right-angled triangle, the square of the hypotenuse (longest side) is equal to the sum of the squares of the other two sides (base and perpendicular ).
- This is represented as: Hypotenuse 2 = Base 2 + Perpendicular 2 .
- Hypotenuse equation is a 2 + b 2 = c 2 . Here, a and b are the legs of the right triangle and c is the hypotenuse.
- The hypotenuse leg theorem states that two triangles are congruent if the hypotenuse and one leg of one right triangle are congruent/equal to the other right triangle's hypotenuse and leg side.
How to Find Hypotenuse?
To find the length of the hypotenuse of a triangle, we will be using the above equation. For that, we should know the values of the base and perpendicular of the triangle. For example, in a right triangle, if the length of the base is 3 units, and the length of the perpendicular side is 4 units, then the length of the hypotenuse can be found by using the formula Hypotenuse 2 = Base 2 + Perpendicular 2 . By substituting the values of the base and perpendicular, we get, Hypotenuse 2 = 3 2 + 4 2 = 9 + 16 = 25. This implies that the length of the hypotenuse is 5 units. This is how we can easily find the length of the hypotenuse by using the hypotenuse equation.
Follow the steps given below to find the hypotenuse length in a right-angled triangle:
- Step 1: Identify the values of base and perpendicular sides.
- Step 2: Substitute the values of base and perpendicular in the formula: Hypotenuse 2 = Base 2 + Perpendicular 2 .
- Step 3: Solve the equation and get the answer.
Let us consider one more example to find the hypotenuse of a triangle. The longest side of the triangle is the hypotenuse and the other two sides of the right triangle are the perpendicular side with a measure of 8 inches, and the base with a measure of 6 inches.

The following formula is helpful to calculate the measure of the hypotenuse → (Hypotenuse) 2 = (Base) 2 + (Perpendicular) 2 = 6 2 + 8 2 = 36 + 64 = 100. This implies, Hypotenuse = √100 = 10 inches. Also, any of the other two sides, the base or the perpendicular side can be easily calculated for the given value of the hypotenuse using the same equation.
Hypotenuse Theorem
The hypotenuse can be related to the other two sides of the right-angled triangle by the Pythagoras theorem. The Pythagoras theorem states that the square of the hypotenuse is equal to the sum of the squares of the base of the triangle, and the square of the altitude of the triangle. Among the three sides of the right triangle, the hypotenuse is the largest side, and Hypotenuse 2 = Base 2 + Altitude 2 . This is known as the hypotenuse theorem . The lengths of the hypotenuse, altitude, and base of the triangle, are together defined as a set called the Pythagorean triplets. A few examples of Pythagorean triples are (5, 4, 3), (10, 8, 6), and (25, 24, 7).
Challenging Questions:
Having understood the concepts related to the hypotenuse of a triangle, now try out these two challenging questions.
- A 5 meters ladder stands on horizontal ground and reaches 3 m up a vertical wall. How far is the foot of the ladder from the wall?
- Town B is 9 km north and 16 km west of town A. What is the shortest distance to go from town A to town B?
► Related Topics:
Check these articles related to the concept of the hypotenuse of a triangle.
- Hypotenuse Calculator
- Area of Right Triangle
- Properties of Triangle
Hypotenuse Examples
Example 1: Find the value of the longest side of a bread slice that is in the shape of a right-angle triangle with a given perpendicular height of 12 inches and the base of 5 inches.
Given dimensions are perpendicular (P) = 12 inches, and base (B) = 5 inches. Putting the given dimensions in the formula H 2 = B 2 + P 2 , we get, H 2 = 5 2 + 12 2 H = √{25+144} = √169 inches H = 13 inches. Therefore the length of the hypotenuse (longest side) of the bread slice is 13 inches.
Example 2: In a right triangle, the hypotenuse is 5 units, and the perpendicular is 4 units. Find the measure of the base of the triangle.
Given dimensions are perpendicular (P) = 4 units, and hypotenuse (H) = 5 units. We know that (H) 2 = (B) 2 + (P) 2 ⇒ (B) 2 = (H) 2 - (P) 2 . Putting the given dimensions in the formula, we get, B 2 = (5) 2 - (4) 2 B = √{25-16} B = √9 = 3 units Therefore, the length of the base is 3 units.
Example 3: How to find the missing hypotenuse of a triangle with base = 7 units and perpendicular = 24 units?
Given dimensions are base (B) = 7 units and perpendicular (P) = 24 units. To find the hypotenuse (H), we will use the equation: (H) 2 = (B) 2 + (P) 2 . Putting the given dimensions in the equation, we get, H 2 = (7) 2 + (24) 2 B = √{49+576} B = √625 = 25 units Therefore, the length of the hypotenuse is 25 units.
go to slide go to slide go to slide

Book a Free Trial Class
Practice Questions on Hypotenuse
go to slide go to slide
FAQs on Hypotenuse
What is the meaning of hypotenuse.
In mathematics, the hypotenuse of a triangle is defined as the longest side of a right triangle. It is the side opposite to the 90-degree angle . It is equal to the square root of the sum of the squares of the other two sides.
What is the Length of the Hypotenuse?
The length of the hypotenuse is greater than the lengths of the other two sides of a right triangle. The square of the hypotenuse length is equal to the sum of squares of the other two sides of the triangle. Mathematically, it can be expressed in the form of an equation as Hypotenuse 2 = Base 2 + Perpendicular 2 .
What is the Hypotenuse Leg Theorem?
The hypotenuse leg theorem states that two right triangles are congruent if the lengths of the hypotenuse and any one of the legs of a triangle are equal to the hypotenuse and the leg of the other triangle.
How to Find the Missing Hypotenuse?
The missing hypotenuse can be easily known if we know the lengths of the other two sides by using the hypotenuse equation: Hypotenuse 2 = Base 2 + Perpendicular 2 . For example, if the base and perpendicular of a right triangle measure 6 units and 8 units respectively, then the hypotenuse is equal to:
Hypotenuse 2 = 6 2 + 8 2
Therefore, hypotenuse = 10 units.
How do you Find the Hypotenuse of a Triangle?
By using the Pythagorean theorem (Hypotenuse) 2 = (Base) 2 + (Altitude) 2 , we can calculate the hypotenuse. If the values of the other two sides are known, the hypotenuse can be easily calculated with this formula.
How do you Find the Longest Side of a Triangle?
The hypotenuse is termed as the longest side of a right-angled triangle. To find the longest side we use the hypotenuse theorem, (Hypotenuse) 2 = (Base) 2 + (Altitude) 2 . For example, a bread slice is given in the shape of a right-angled triangle. If the base is 4 inches and the height is 3 inches, then the hypotenuse is (H) 2 = (4) 2 + (3) 2 = √{16+9} = √25 = 5 inches.
How to Find Hypotenuse with Angle and Side?
If an angle and a side are known, then we can calculate hypotenuse by applying the formula of trigonometric ratios . If A is the angle known, then we have,
- sin A = Perpendicular/Hypotenuse
- cos A = Base/Hypotenuse
So, if the length of the base is given, then the cos formula can be used and if height is known then the sin formula can be used to find the hypotenuse length.
What is the Difference between the Hypotenuse and Other Sides of a Triangle?
The hypotenuse is the largest side of the triangle. The other two sides are the base and the altitude of the right triangle. These are related to each other with the formula (Hypotenuse) 2 = (Base) 2 + (Altitude) 2 .
How is the Hypotenuse Related to the Right Angle?
The hypotenuse is the side opposite to the right angle. The hypotenuse is the largest side of a right triangle and is drawn opposite to the largest angle, which is the right angle.
Can a Hypotenuse be Drawn for Any Triangle?
The hypotenuse can be drawn only for a right triangle, and not for any other triangle. The side opposite to the 90° angle is the hypotenuse. And since a right angle is there in a right triangle, it has a hypotenuse.
How to Calculate Hypotenuse?
The formula to calculate the hypotenuse is (Hypotenuse) 2 = (Base) 2 + (Altitude) 2 . The largest side of the right triangle is the hypotenuse, and it can be calculated if the other two sides are known.
Right Triangle Calculator
Please provide 2 values below to calculate the other values of a right triangle. If radians are selected as the angle unit, it can take values such as pi/3, pi/4, etc.
| a = | ∠α = | ||
| b = | ∠β = | ||
| c = | h = | ||
| A = | area | ||
| P = | perimeter | ||
Related Triangle Calculator | Pythagorean Theorem Calculator
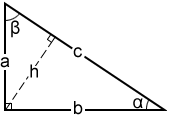
Right triangle
A right triangle is a type of triangle that has one angle that measures 90°. Right triangles, and the relationships between their sides and angles, are the basis of trigonometry.
In a right triangle, the side that is opposite of the 90° angle is the longest side of the triangle, and is called the hypotenuse. The sides of a right triangle are commonly referred to with the variables a, b, and c, where c is the hypotenuse and a and b are the lengths of the shorter sides. Their angles are also typically referred to using the capitalized letter corresponding to the side length: angle A for side a, angle B for side b, and angle C (for a right triangle this will be 90°) for side c, as shown below. In this calculator, the Greek symbols α (alpha) and β (beta) are used for the unknown angle measures. h refers to the altitude of the triangle, which is the length from the vertex of the right angle of the triangle to the hypotenuse of the triangle. The altitude divides the original triangle into two smaller, similar triangles that are also similar to the original triangle.
If all three sides of a right triangle have lengths that are integers, it is known as a Pythagorean triangle. In a triangle of this type, the lengths of the three sides are collectively known as a Pythagorean triple. Examples include: 3, 4, 5; 5, 12, 13; 8, 15, 17, etc.
Area and perimeter of a right triangle are calculated in the same way as any other triangle. The perimeter is the sum of the three sides of the triangle and the area can be determined using the following equation:

































IMAGES
VIDEO
COMMENTS
1. TD Bank: This stock has a proven history of profitability. When it comes to making money with bank stocks, Toronto-Dominion Bank (TD 0.79%) is a prime case study. Over the last 30 years, shares ...
Apple CEO Tim Cook is living out the Hollywood movie executive fantasy in Italy right now. Katie Balevic. 2024-09-01T19:25:18Z ... An icon in the shape of an angle pointing down.
Use the Pythagorean theorem to calculate the hypotenuse from the right triangle sides. Take a square root of sum of squares: c = √(a² + b²) Given an angle and one leg. c = a / sin(α) = b / sin(β), explained in our law of sines calculator. Given the area and one leg. As the area of a right triangle is equal to a × b / 2, then.
A Right Triangle's Hypotenuse. The hypotenuse is the largest side in a right triangle and is always opposite the right angle. (Only right triangles have a hypotenuse ). The other two sides of the triangle, AC and CB are referred to as the 'legs'. In the triangle above, the hypotenuse is the side AB which is opposite the right angle, ∠C ∠ C .
The hypotenuse side is opposite to the right angle, which is the biggest angle of all the three angles in a right triangle. Basically, the hypotenuse is the property of only the right triangle and no other triangle. Now, this is better explained when we learn about the right-angled theorem or Pythagoras Theorem or Pythagorean theorem. These ...
By Pythagorean Theorem, (Hypotenuse) 2 = (Base) 2 + (Height) 2. Hypotenuse = √ (Base) 2 + (Height) 2. Thus, mathematically, hypotenuse is the sum of the square of base and height of a right triangle. The above formula is also written as, c = √a 2 + b 2, here c = hypotenuse, a = height, b = base. Let us solve some problems to understand the ...
How to Find the Hypotenuse for a 30 60 90 Right Triangle. A 30 60 90 triangle is a special right triangle that has one 30° interior angle, one 60° interior angle, and one right interior angle.. In this special case, the length of the hypotenuse is always equal to two times the length of the shortest leg a of the triangle. Note, the shortest leg will always be opposite the 30° interior angle.
Learn how to identify and use the hypotenuse, opposite, and adjacent sides of right triangles in trigonometry. Khan Academy offers free, interactive lessons on math and more.
For complementary angle of θ, the labels of the 2 sides are reversed. Example: Identify the hypotenuse, adjacent side and opposite side in the following triangle: a) for angle x. b) for angle y. Solution: a) For angle x: AB is the hypotenuse, AC is the adjacent side , and BC is the opposite side. b) For angle y: AB is the hypotenuse, BC is the ...
Right triangles can be identified with a box at their right angle. This box is the notation that the angle is exactly 90 degrees. There are two types of special right triangles, a 30, 60, 90 ...
Right angle is equal to 90 degrees. In a right angled triangle, the three sides are called: Perpendicular, Base(Adjacent) and Hypotenuse(Opposite). Perpendicular is the side that makes right angle with the base of the triangle. The largest side side which is opposite to the right-angle(90 degree) is known as the Hypotenuse.
For example, let's look at the following figure of a right triangle: In this triangle, c is the hypotenuse since it is the side opposite the right angle. Therefore, the Pythagorean theorem tells us: { {c}^2}= { {a}^2}+ { {b}^2} c2 = a2 +b2. where c is the length of the hypotenuse, a and b are the lengths of the other two sides.
This also makes sense because the internal angles of a triangle sum to 180°. Since all triangles have 3 sides and 3 internal angles, it is impossible for a right triangle to have another angle that is greater than or equal to 90°, because the third angle would have to be 0° or have a negative angle measurement. How to find the hypotenuse
A right-angled triangle and its hypotenuse. In geometry, a hypotenuse is the side of a right triangle opposite the right angle. [1] It is the longest side of any such triangle; the two other shorter sides of such a triangle are called catheti or legs.The length of the hypotenuse can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the ...
To derive an equation or a formula of the hypotenuse, years ago there was an interesting fact revealed about triangles. Hypotenuse equation: The fact states that with a right-angled triangle or a triangle with a 90º angle, squares can be framed using each of the three sides of the triangle.After putting squares against each side, it was observed that the biggest square has the exact same area ...
The 45°-45°-90° triangle, also referred to as an isosceles right triangle, since it has two sides of equal lengths, is a right triangle in which the sides corresponding to the angles, 45°-45°-90°, follow a ratio of 1:1:√ 2. Like the 30°-60°-90° triangle, knowing one side length allows you to determine the lengths of the other sides ...
A 45-45-90 right triangle has angles of 45, 45, and 90 degrees, and is also called an Isosceles Right Triangle. It occurs frequently on standardized tests, and is a very easy triangle to solve. The ratio between the sides of this triangle is 1:1:Sqrt(2) , which means that the length of the legs are equal, and the length of the hypotenuse is ...
We will apply these properties, postulates, and. theorems to help drive our mathematical proofs in a very logical, reason-based way. Before we begin, we must introduce the concept of congruency. Angles are congruent. if their measures, in degrees, are equal. Note: "congruent" does not. mean "equal.". While they seem quite similar ...
This right angle limits the possible measurements of the other two angles. Together they must add up to 90° because all interior angles of any triangle -- right, scalene, obtuse -- must add to 180°. Subtracting the one right angle from 180° leaves only 90° to be shared by the two remaining angles, making both of them acute angles.
The Pythagorean Theorem tells us that the relationship in every right triangle is: a2 + b2 = c2 a 2 + b 2 = c 2. Example. C2 = 62 + 42 C 2 = 6 2 + 4 2. C2 = 36 + 16 C 2 = 36 + 16. C2 = 52 C 2 = 52. C = 52−−√ C = 52. C ≈ 7.2 C ≈ 7.2. There are a couple of special types of right triangles, like the 45°-45° right triangles and the 30 ...
A right triangle (or right-angled triangle) is a triangle in which one of the three internal angles is a right angle (90 ° \hspace{0.2em} 90 \degree \hspace{0.2em} 90°). The longest side in a right triangle (known as the hypotenuse) is the side opposite the right angle.
The other two angles will clearly be smaller than the right angle because the sum of all angles in a triangle is always 180°. In a right-angled triangle, we define the sides in a special way. The side opposing the right angle is always the biggest in the triangle and receives the name of "hypotenuse". The other two sides are called catheti.
It is to be noted here that since the sum of interior angles in a triangle is 180 degrees, only 1 of the 3 angles can be a right angle. Read more: Right Angled Triangle. If the other two angles are equal, that is 45 degrees each, the triangle is called an isosceles right-angled triangle. However, if the other two angles are unequal, it is a ...
Find the size of angle a°. Step 1 The two sides we know are A djacent (6,750) and H ypotenuse (8,100). Step 2 SOH CAH TOA tells us we must use C osine. Step 3 Calculate Adjacent / Hypotenuse = 6,750/8,100 = 0.8333. Step 4 Find the angle from your calculator using cos-1 of 0.8333: cos a° = 6,750/8,100 = 0.8333.
Right triangles are triangles with one 90-degree angle. The two sides that meet and form the right angle are called the triangle's legs, and the side facing (or opposite) the right angle is the ...