
- Math Forum/Help
- Problem Solver
- College Math
- Quadratic Equations


Quadratic Equations: Very Difficult Problems with Solutions
Site Navigation
Latest stories, 20 grade-school math questions so hard you'll wonder how you graduated, seriously, who can do these.

Unless you grew up to be an engineer, a banker, or an accountant, odds are that elementary and middle school math were the bane of your existence. You would study relentlessly for weeks for those silly standardized tests—and yet, come exam day, you'd still somehow have no idea what any of the equations or hard math problems were asking for. Trust us, we get it.
While logic might lead you to believe that your math skills have naturally gotten better as you've aged, the unfortunate reality is that, unless you've been solving algebra and geometry problems on a daily basis, the opposite is more likely the case.
Don't believe us? Then put your number crunching wisdom to the test with these tricky math questions taken straight from grade school tests and homework assignments and see for yourself.
1. Question: What is the number of the parking space covered by the car?
This tricky math problem went viral a few years back after it appeared on an entrance exam in Hong Kong... for six-year-olds. Supposedly the students had just 20 seconds to solve the problem!
Answer: 87.
Believe it or not, this "math" question actually requires no math whatsoever. If you flip the image upside down, you'll see that what you're dealing with is a simple number sequence.
2. Question: Replace the question mark in the above problem with the appropriate number.
This problem shouldn't be too difficult to solve if you play a lot of sudoku.
All of the numbers in every row and column add up to 15! (Also, 6 is the only number not represented out of numbers 1 through 9.)
3. Question: Find the equivalent number.
This problem comes straight from a standardized test given in New York in 2014.
You're forgiven if you don't remember exactly how exponents work. In order to solve this problem, you simply need to subtract the exponents (4-2) and solve for 3 2 , which expands into 3 x 3 and equals 9.
4. Question: How many small dogs are signed up to compete in the dog show?
This question comes directly from a second grader's math homework. Yikes.
Answer: 42.5 dogs.
In order to figure out how many small dogs are competing, you have to subtract 36 from 49 and then divide that answer, 13, by 2, to get 6.5 dogs, or the number of big dogs competing. But you're not done yet! You then have to add 6.5 to 36 to get the number of small dogs competing, which is 42.5. Of course, it's not actually possible for half a dog to compete in a dog show, but for the sake of this math problem let's assume that it is.
5. Question: Find the area of the red triangle.
This question was used in China to identify gifted 5th graders. Supposedly, some of the smart students were able to solve this in less than one minute.
In order to solve this problem, you need to understand how the area of a parallelogram works. If you already know how the area of a parallelogram and the area of a triangle are related, then adding 79 and 10 and subsequently subtracting 72 and 8 to get 9 should make sense—but if you're still confused, then check out this YouTube video for a more in-depth explanation.
6. Question: How tall is the table?
YouTuber MindYourDecisions adapted this mind-boggling math question from a similar one found on an elementary school student's homework in China.
Answer: 150 cm.
Since one measurement includes the cat's height and subtracts the turtle's and the other does the opposite, you can essentially just act like the two animals aren't there. Therefore, all you have to do is add the two measurements—170 cm and 130 cm—together and divided them by 2 to get the table's height, 150 cm.
7. Question: If the cost of a bat and a baseball combined is $1.10 and the bat costs $1.00 more than the ball, how much is the ball?
This problem, mathematically speaking, is very similar to one of the other ones on this list.
Answer: $0.05.
Think back to that problem about the dogs at the dog show and use the same logic to solve this problem. All you have to do is subtract $1.00 from $1.10 and then divide that answer, $0.10 by 2, to get your final answer, $0.05.
8. Question: When is Cheryl's birthday?
If you're having trouble reading that, see here:
"Albert and Bernard just became friends with Cheryl, and they want to know when her birthday is. Cheryl gives them a list of 10 possible dates.
May 15 May 16 May 19
June 17 June 18
July 14 July 16
August 14 August 15 August 17
Cheryl then tells Albert and Bernard separately the month and the day of her birthday respectively.
Albert: I don't know when Cheryl's birthday is, but I know that Bernard doesn't not know too.
Bernard: At first I don't know when Cheryl's birthday is, but I know now.
Albert: Then I also know when Cheryl's birthday is.
So when is Cheryl's birthday?"
It's unclear why Cheryl couldn't just tell both Albert and Bernard the month and day she was born, but that's irrelevant to solving this problem.
Answer: July 16.
Confused about how one could possibly find any answer to this question? Don't worry, so was most of the world when this question, taken from a Singapore and Asian Schools Math Olympiad competition, went viral a few years ago. Thankfully, though, the New York Times explains step-by-step how to get to July 16, and you can read their detailed deduction here.
9. Question: Find the missing letter.
This one comes from a first grader's homework.
Answer: The missing letter is J.
When you add together the values given for S, B, and G, the sum comes out to 40, and making the missing letter J (which has a value of 14) makes the other diagonal's sum the same.
10. Question: Solve the equation.
This problem might look easy, but a surprising number of adults are unable to solve it correctly.
Start by solving the division part of the equation. In order to do that, in case you forgot, you have to flip the fraction and switch from division to multiplication, thus getting 3 x 3 = 9. Now you have 9 - 9 + 1, and from there you can simply work from left to right and get your final answer: 1.
11. Question: Where should a line be drawn to make the below equation accurate?
5 + 5 + 5 + 5 = 555.
Answer: A line should be drawn on a "+" sign.
When you draw a slanted line in the upper left quadrant of a "+," it becomes the number 4 and the equation thusly becomes 5 + 545 + 5 = 555.
12. Question: Solve the unfinished equation.
Try to figure out what all of the equations have in common.
Answer: 4 = 256.
The formula used in each equation is 4 x = Y. So, 4 1 = 4, 4 2 = 16, 4 3 = 64, and 4 4 = 256.
13. Question: How many triangles are in the image above?
When Best Life first wrote about this deceiving question, we had to ask a mathematician to explain the answer!
Answer: 18.
Some people get stumped by the triangles hiding inside of the triangles and others forget to include the giant triangle housing all of the others. Either way, very few individuals—even math teachers—have been able to find the correct answer to this problem. And for more questions that will put your former education to the test, check out these 30 Questions You'd Need to Ace to Pass 6th Grade Geography.
14. Question: Add 8.563 and 4.8292.
Adding two decimals together is easier than it looks.
Answer: 13.3922.
Don't let the fact that 8.563 has fewer numberrs than 4.8292 trip you up. All you have to do is add a 0 to the end of 8.563 and then add like you normally would.
15. Question: There is a patch of lily pads on a lake. Every day, the patch doubles in size...
... If it takes 48 days for the patch to cover the entire lake, how long would it take for the patch to cover half of the lake?
Answer: 47 days.
Most people automatically assume that half of the lake would be covered in half the time, but this assumption is wrong. Since the patch of pads doubles in size every day, the lake would be half covered just one day before it was covered entirely.
16. Question: How many feet are in a mile?
This elementary school-level problem is a little less problem solving and a little more memorization.
Answer: 5,280.
This was one of the questions featured on the popular show Are You Smarter Than a 5th Grader?
17. Question: What value of "x" makes the equation below true?
-15 + (-5x) = 0
Answer: -3.
You'd be forgiven for thinking that the answer was 3. However, since the number alongside x is negative, we need x to be negative as well in order to get to 0. Therefore, x has to be -3.
18. Question: What is 1.92 divided by 3?
You might need to ask your kids for help on this one.
Answer: 0.64.
In order to solve this seemingly simple problem, you need to remove the decimal from 1.92 and act like it isn't there. Once you've divided 192 by 3 to get 64, you can put the decimal place back where it belongs and get your final answer of 0.64.
19. Question: Solve the math equation above.
Don't forget about PEMDAS!
Using PEMDAS (an acronym laying out the order in which you solve it: "parenthesis, exponents, multiplication, division, addition, subtraction"), you would first solve the addition inside of the parentheses (1 + 2 = 3), and from there finish the equation as it's written from left to right.
20. Question: How many zombies are there?
Finding the answer to this final question will require using fractions.
Answer: 34.
Since we know that there are two zombies for every three humans and that 2 + 3 = 5, we can divide 85 by 5 to figure out that in total, there are 17 groups of humans and zombies. From there, we can then multiply 17 by 2 and 3 and learn that there are 34 zombies and 51 humans respectively. Not too bad, right?
To discover more amazing secrets about living your best life, click here to follow us on Instagram!
This Is the Most Effective Weight-Loss Drug
165 good roasts that will absolutely destroy, the healthiest vegetable you're probably not eating, 10 easy ways to feel more balanced.
- Top Questions
Convert the following readings of pressureto kPa absolute, assuming that the barometer reads 760mm Hg:...
Show that an element and its inverse have the same order in any group.
A cubic block of wood, 10.0 cm on each side, floats at the interface between...
An ice cube tray of negligible mass contains 0.315 kg of water at17.7∘. How much...
An open tank has a vertical partition and on one side contains gasoline with a...
A 100g cube of ice at 0C is dropped into 1.0kg of water thatwas originally...
Complete the equation of the line through (2, 1) and (5, -8). Use exact numbers.
Write a function based on the given parent function and transformations in the given order....
How many solutions does the equationx1+x2+x3=13have wherex1,x2,andx3are non negative integers less than 6.
Determine whether f : Z×Z→Z is onto if a) f(m,n)=2m−nb) b) f(m,n)=m2−n2 c) f(m,n)=m+n+1 d)...
The base of S is an elliptical region with boundary curve 9x2+4y2=36. Cross-sections perpendicular to...
Create a graph of y=2x−6. Construct a graph corresponding to the linear equation y=2x−6.
Use the graphs of f and g to graph h(x) = (f + g)(x). (Graph...
find expressions for the quadratic functions whose graphs are shown. f(x)=? g(x)=?
Find the volume V of the described solid S. A cap of a sphere with...
Find a counterexample to show that each statement is false. The sum of any three...
Read the numbers and decide what the next number should be. 5 15 6 18...
In how many different orders can five runners finish a race if no ties are...
A farmer plants corn and wheat on a 180 acre farm. He wants to plant...
Find the distance between (0, 0) and (-3, 4) pair of points. If needed, show...
Whether each of these functions is a bijection from R to R.a)f(x)=−3x+4b)f(x)=−3x2+7c)f(x)=x+1x+2d)f(x)=x5+1
Find two numbers whose difference is 100 and whose product is a minimum.
Find an expression for the function whose graph is the given curve. The line segment...
Prove or disprove that if a and b are rational numbers, then ab is also...
How to find a rational number halfway between any two rational numbers given infraction form...
Fill in the blank with a number to make the expression a perfect square x2−6x+?
Look at this table: x y 1–2 2–4 3–8 4–16 5–32 Write a linear (y=mx+b),...
Part a: Assume that the height of your cylinder is 8 inches. Think of A...
The graph of a function f is shown. Which graph is an antiderivative of f?
A rectangle has area 16m2 . Express the perimeter of the rectangle as a function...
Find the equation of the quadratic function f whose graph is shown below. (5, −2)
Use the discriminant, b2−4ac, to determine the number of solutions of the following quadratic equation....
How many solutions does the equation ||2x-3|-m|=m have if m>0?
If a system of linear equations has infinitely many solutions, then the system is called...
A bacteria population is growing exponentially with a growth factor of 16 each hour.By what...
A system of linear equations with more equations than unknowns is sometimes called an overdetermined...
Express the distance between the numbers 2 and 17 using absolute value. Then find the...
Find the Laplace transform of f(t)=(sint–cost)2
Express the interval in terms of an inequality involving absolute value. (0,4)
A function is a ratio of quadratic functions and has a vertical asymptote x =4...
how do you graph y > -2
Find the weighted average of a data set where 10 has a weight of 5,...
The population of California was 29.76 million in 1990 and 33.87 million in 2000. Assume...
The population of a region is growing exponentially. There were 10 million people in 1980...
Two cables BG and BH are attached to the frame ACD as shown.Knowing that the...
A bird flies in the xy-plane with a position vector given by r→=(αt−βt3)i^+γt2j^, with α=2.4...
A movie stuntman (mass 80.0kg) stands on a window ledge 5.0 mabove the floor. Grabbing...
Solve the following linear congruence, 25x≡15(bmod29)
For the equation, a. Write the value or values of the variable that make a...
Which of the following statements is/are correct about logistic regression? (There may be more than...
Compute 4.659×104−2.14×104. Round the answer appropriately. Express your answer as an integer using the proper...
Find the 52nd term of the arithmetic sequence -24,-7, 10
Find the 97th term of the arithmetic sequence 17, 26, 35,
An equation that expresses a relationship between two or more variables, such as H=910(220−a), is...
The football field is rectangular. a. Write a polynomial that represents the area of the...
The equation 1.5r+15=2.25r represents the number r of movies you must rent to spend the...
While standing on a ladder, you drop a paintbrush. The function represents the height y...
When does data modeling use the idea of a weak entity? Give definitions for the...
Write an equation of the line passing through (-2, 5) and parallel to the line...
Find a polar equation for the curve represented by the given Cartesian equation. y =...
Find c such that fave=f(c)
List five integers that are congruent to 4 modulo 12.
A rectangular package to be sent by a postal service can have a maximum combined...
A juggler throws a bowling pin straight up with an initial speed of 8.20 m/s....
The One-to-One Property of natural logarithms states that if ln x = ln y, then...
Find an equation of a parabola that has curvature 4 at the origin.
Find a parametric representation of the solution set of the linear equation. 3x − 1/2y...
Find the product of the complex number and its conjugate. 2-3i
Find the prime factorization of 10!.
Find a polynomial f(x) of degree 5 that has the following zeros. -3, -7, 5...
True or False. The domain of every rational function is the set of all real...
What would be the most efficient step to suggest to a student attempting to complete...
Write a polynomial, P(x), in factored form given the following requirements. Degree: 4 Leading coefficient...
Give a geometric description of the set of points in space whose coordinates satisfy the...
Use the Cauchy-Riemann equations to show that f(z)=z― is not analytic.
Find the local maximum and minimum values and saddle points of the function. If you...
a) Evaluate the polynomial y=x3−7x2+8x−0.35 at x=1.37 . Use 3-digit arithmetic with chopping. Evaluate the...
The limit represents f'(c) for a function f and a number c. Find f and...
A man 6 feet tall walks at a rate of 5 feet per second away...
Find the Maclaurin series for the function f(x)=cos4x. Use the table of power series for...
Suppose that a population develops according to the logistic equation dPdt=0.05P−0.0005P2 where t is measured...
Find transient terms in this general solution to a differential equation, if there are any...
Find the lengths of the sides of the triangle PQR. Is it a right triangle?...
Use vectors to decide whether the triangle with vertices P(1, -3, -2), Q(2, 0, -4),...
Find a path that traces the circle in the plane y=5 with radius r=2 and...
a. Find an upper bound for the remainder in terms of n.b. Find how many...
Find two unit vectors orthogonal to both j−k and i+j.
Obtain the Differential equations: parabolas with vertex and focus on the x-axis.
The amount of time, in minutes, for an airplane to obtain clearance for take off...
Use the row of numbers shown below to generate 12 random numbers between 01 and...
Here’s an interesting challenge you can give to a friend. Hold a $1 (or larger!)...
A random sample of 1200 U.S. college students was asked, "What is your perception of...
The two intervals (114.4, 115.6) and (114.1, 115.9) are confidence intervals (The same sample data...
How many different 10 letter words (real or imaginary) can be formed from the following...
Assume that σ is unknown, the lower 100(1−α)% confidence bound on μ is: a) μ≤x―+tα,n−1sn...
A simple random sample of 60 items resulted in a sample mean of 80. The...
Decresing the sample size, while holding the confidence level and the variance the same, will...
A privately owned liquor store operates both a drive-n facility and a walk-in facility. On...
Show that the equation represents a sphere, and find its center and radius. x2+y2+z2+8x−6y+2z+17=0
Describe in words the region of R3 represented by the equation(s) or inequality. x=5
Suppose that the height, in inches, of a 25-year-old man is a normal random variable...
Find the value and interest earned if $8906.54 is invested for 9 years at %...
Which of the following statements about the sampling distribution of the sample mean is incorrect?...
The random variable x stands for the number of girls in a family of four...
The product of the ages, in years, of three (3) teenagers os 4590. None of...
A simple random sample size of 100 is selected from a population with p=0.40 What...
Which of the following statistics are unbiased estimators of population parameters? Choose the correct answer...
The probability distribution of the random variable X represents the number of hits a baseball...
Let X be a random variable with probability density function.f(x)={c(1−x2)−1<x<10otherwise(a) What is the value of...
A survey of 4826 randomly selected young adults (aged 19 to 25) asked, "What do...
The monthly worldwide average number of airplane crashes of commercial airlines is 2.2. What is...
Given that z is a standard normal random variable, compute the following probabilities.a.P(z≤−1.0)b.P(z≥−1)c.P(z≥−1.5)d.P(−2.5≤z)e.P(−3<z≤0)
Given a standard normal distribution, find the area under the curve that lies(a) to the...
Chi-square tests are best used for which type of dependent variable? nominal, ordinal ordinal interval...
True or False 1.The goal of descriptive statistics is to simplify, summarize, and organize data....
What is the difference between probability distribution and sampling distribution?
A weather forecaster predicts that the temperature in Antarctica will decrease 8∘F each hour for...
The tallest person who ever lived was approximately 8 feet 11 inches tall. a) Write...
An in-ground pond has the shape of a rectangular prism. The pond has a depth...
The average zinc concentration recovered from a sample of measurements taken in 36 different locations...
Why is it important that a sample be random and representative when conducting hypothesis testing?...
Which of the following is true about the sampling distribution of means? A. Shape of...
Give an example of a commutative ring without zero-divisors that is not an integral domain.
List all zero-divisors in Z20. Can you see relationship between the zero-divisors of Z20 and...
Find the integer a such that a≡−15(mod27) and −26≤a≤0
Explain why the function is discontinuous at the given number a. Sketch the graph of...
Two runners start a race at the same time and finish in a tie. Prove...
Which of the following graphs represent functions that have inverse functions?
find the Laplace transform of f (t). f(t)=tsin3t
Find Laplace transforms of sinh3t cos22t
find the Laplace transform of f (t). f(t)=t2cos2t
The Laplace transform of the product of two functions is the product of the Laplace...
The Laplace transform of u(t−2) is (a) 1s+2 (b) 1s−2 (c) e2ss(d)e−2ss
Find the Laplace Transform of the function f(t)=eat
Explain First Shift Theorem & its properties?
Solve f(t)=etcost
Find Laplace transform of the given function te−4tsin3t
Reduce to first order and solve:x2y″−5xy′+9y=0 y1=x3
(D3−14D+8)y=0
A thermometer is taken from an inside room to the outside ,where the air temperature...
Find that solution of y′=2(2x−y) which passes through the point (0, 1).
Radium decomposes at a rate proportional to the amount present. In 100 years, 100 mg...
Let A, B, and C be sets. Show that (A−B)−C=(A−C)−(B−C)
Suppose that A is the set of sophomores at your school and B is the...
In how many ways can a 10-question true-false exam be answered? (Assume that no questions...
Is 2∈{2}?
How many elements are in the set { 2,2,2,2 } ?
How many elements are in the set { 0, { { 0 } }?
Draw the Hasse diagram representing the partial ordering {(a, b) | a divides b} on...
Flux through a Cube (Eigure 1) A cube has one corner at the origin and...
A well-insulated rigid tank contains 3 kg of saturated liquid-vapor mixture of water at 200...
A water pump that consumes 2 kW of electric power when operating is claimed to...
A hollow, conducting sphere with an outer radius of 0.250 m and an inner radius...
In a truck-loading station at a post office, a small 0.200-kg package is released from...
The magnetic fieldB→in acertain region is 0.128 ,and its direction is that of the z-axis...
A marble moves along the x-axis. The potential-energy functionis shown in Fig. 1a) At which...
A proton is released in a uniform electric field, and it experiences an electric force...
A potters wheel having a radius of 0.50 m and a moment of inertia of12kg⋅m2is...
Two spherical objects are separated by a distance of 1.80×10−3m. The objects are initially electrically...
An airplane pilot sets a compass course due west and maintainsan airspeed of 220 km/h....
Resolve the force F2 into components acting along the u and v axes and determine...
A conducting sphere of radius 0.01m has a charge of1.0×10−9Cdeposited on it. The magnitude of...
Starting with an initial speed of 5.00 m/s at a height of 0.300 m, a...
In the figure a worker lifts a weightωby pulling down on a rope with a...
A stream of water strikes a stationary turbine bladehorizontally, as the drawing illustrates. The incident...
Until he was in his seventies, Henri LaMothe excited audiences by belly-flopping from a height...
A radar station, located at the origin of xz plane, as shown in the figure...
Two snowcats tow a housing unit to a new location at McMurdo Base, Antarctica, as...
You are on the roof of the physics building, 46.0 m above the ground. Your...
A block is on a frictionless table, on earth. The block accelerates at5.3ms2when a 10...
A 0.450 kg ice puck, moving east with a speed of3.00mshas a head in collision...
A uniform plank of length 2.00 m and mass 30.0 kg is supported by three...
An adventurous archaeologist crosses between two rock cliffs by slowly going hand-over-hand along a rope...
A ski tow operates on a 15.0 degrees slope of lenth 300m. The rope moves...
Two blocks with masses 4.00 kg and 8.00 kg are connected by string and slide...
From her bedroom window a girl drops a water-filled balloon to the ground 6.0 m...
A 730-N man stands in the middle of a frozen pond of radius 5.0 m....
A 5.00 kg package slides 1.50 m down a long ramp that is inclined at12.0∘below...
Ropes 3m and 5m in length are fastened to a holiday decoration that is suspended...
A skier of mass 70 kg is pulled up a slope by a motor driven...
A 1.0 kg ball and a 2.0 kg ball are connected by a 1.0-m-long rigid,...
A sled with rider having a combined mass of 120 kg travels over the perfectly...
A 7.00- kg bowling ball moves at 3.00 m/s. How fast must a 2.45- g...
Two point chargesq1=+2.40nC andq2=−6.50nC are 0.100 m apart. Point A is midway between them and...
A block of mass m slides on a horizontal frictionless table with an initial speed...
A space traveler weights 540 N on earth. what will the traveler weigh on another...
A block of mass m=2.20 kg slides down a 30 degree incline which is 3.60...
A weatherman carried an aneroid barometer from the groundfloor to his office atop a tower....
If a negative charge is initially at rest in an electric field, will it move...
A coin with a diameter of 2.40cm is dropped on edge on to a horizontal...
An atomic nucleus initially moving at 420 m/s emits an alpha particle in the direction...
An 80.0-kg skydiver jumps out of a balloon at an altitude of1000 m and opens...
A 0.145 kg baseball pitched at 39.0 m/s is hit on a horizontal line drive...
A 1000 kg safe is 2.0 m above a heavy-duty spring when the rope holding...
A 500 g ball swings in a vertical circle at the end of a1.5-m-long string....
A rifle with a weight of 30 N fires a 5.0 g bullet with a...
The tires of a car make 65 revolutions as the car reduces its speed uniformly...
A 2.0- kg piece of wood slides on the surface. The curved sides are perfectly...
A 292 kg motorcycle is accelerating up along a ramp that is inclined 30.0° above...
A projectile is shot from the edge of a cliff 125 m above ground level...
A lunch tray is being held in one hand, as the drawing illustrates. The mass...
The initial velocity of a car, vi, is 45 km/h in the positivex direction. The...
An Alaskan rescue plane drops a package of emergency rations to a stranded party of...
Raindrops make an angle theta with the vertical when viewed through a moving train window....
A 0.50 kg ball that is tied to the end of a 1.1 m light...
If the coefficient of static friction between your coffeecup and the horizontal dashboard of your...
A car is initially going 50 ft/sec brakes at a constant rate (constant negative acceleration),...
A swimmer is capable of swimming 0.45m/s in still water (a) If sheaim her body...
A block is hung by a string from inside the roof of avan. When the...
A race driver has made a pit stop to refuel. Afterrefueling, he leaves the pit...
A relief airplane is delivering a food package to a group of people stranded on...
The eye of a hurricane passes over Grand Bahama Island. It is moving in a...
An extreme skier, starting from rest, coasts down a mountainthat makes an angle25.0∘with the horizontal....
Four point charges form a square with sides of length d, as shown in the...
In a scene in an action movie, a stuntman jumps from the top of one...
The spring in the figure (a) is compressed by length delta x . It launches...
An airplane propeller is 2.08 m in length (from tip to tip) and has a...
A helicopter carrying dr. evil takes off with a constant upward acceleration of5.0ms2. Secret agent...
A 15.0 kg block is dragged over a rough, horizontal surface by a70.0 N force...
A box is sliding with a speed of 4.50 m/s on a horizontal surface when,...
3.19 Win the Prize. In a carnival booth, you can win a stuffed giraffe if...
A car is stopped at a traffic light. It then travels along a straight road...
a. When the displacement of a mass on a spring is12A, what fraction of the...
At a certain location, wind is blowing steadily at 10 m/s. Determine the mechanical energy...
A jet plane lands with a speed of 100 m/s and can accelerate at a...
In getting ready to slam-dunk the ball, a basketball player starts from rest and sprints...
An antelope moving with constant acceleration covers the distance between two points 70.0 m apart...
A bicycle with 0.80-m-diameter tires is coasting on a level road at 5.6 m/s. A...
The rope and pulley have negligible mass, and the pulley is frictionless. The coefficient of...
A proton with an initial speed of 800,000 m/s is brought to rest by an...
The volume of a cube is increasing at the rate of 1200 cm supmin at...
An airplane starting from airport A flies 300 km east, then 350 km at 30...
To prove: In the following figure, triangles ABC and ADC are congruent. Given: Figure is...
Conduct a formal proof to prove that the diagonals of an isosceles trapezoid are congruent....
The distance between the centers of two circles C1 and C2 is equal to 10...
Segment BC is Tangent to Circle A at Point B. What is the length of...
Find an equation for the surface obtained by rotating the parabola y=x2 about the y-axis.
Find the area of the parallelogram with vertices A(-3, 0), B(-1 , 3), C(5, 2),...
If the atomic radius of lead is 0.175 nm, find the volume of its unit...
At one point in a pipeline the water’s speed is 3.00 m/s and the gauge...
Find the volume of the solid in the first octant bounded by the coordinate planes,...
A paper cup has the shape of a cone with height 10 cm and radius...
A light wave has a 670 nm wavelength in air. Its wavelength in a transparent...
An airplane pilot wishes to fly due west. A wind of 80.0 km/h (about 50...
Find the equation of the sphere centered at (-9, 3, 9) with radius 5. Give...
Determine whether the congruence is true or false. 5≡8 mod 3
Find all whole number solutions of the congruence equation. (2x+1)≡5 mod 4
Determine whether the congruence is true or false. 100≡20 mod 8
I want example of an undefined term and a defined term in geometry and explaining...
Two fair dice are rolled. Let X equal the product of the 2dice. Compute P{X=i}...
Suppose that two defective refrigerators have been included in a shipment of six refrigerators. The...
Based on the Normal model N(100, 16) describing IQ scores, what percent of peoples
The probability density function of the net weight in pounds of a packaged chemical herbicide...
Let X represent the difference between the number of heads and the number of tails...
An urn contains 3 red and 7 black balls. Players A and B withdraw balls...
80% A poll is given, showing are in favor of a new building project. 8...
The probability that the San Jose Sharks will win any given game is 0.3694 based...
Find the value of P(X=7) if X is a binomial random variable with n=8 and...
Find the value of P(X=8) if X is a binomial random variable with n=12 and...
On a 8 question multiple-choice test, where each question has 2 answers, what would be...
If you toss a fair coin 11 times, what is the probability of getting all...
A coffee connoisseur claims that he can distinguish between a cup of instant coffee and...
Two firms V and W consider bidding on a road-building job, which may or may...
Two cards are drawn without replacement from an ordinary deck, find the probability that the...
In August 2012, tropical storm Isaac formed in the Caribbean and was headed for the...
A local bank reviewed its credit card policy with the intention of recalling some of...
The accompanying table gives information on the type of coffee selected by someone purchasing a...
A batch of 500 containers for frozen orange juice contains 5 that are defective. Two...
The probability that an automobile being filled with gasoline also needs an oil change is...
Let the random variable X follow a normal distribution with μ=80 and σ2=100. a. Find...
A card is drawn randomly from a standard 52-card deck. Find the probability of the...
The next number in the series 38, 36, 30, 28, 22 is ?
What is the coefficient of x8y9 in the expansion of (3x+2y)17?
A boat on the ocean is 4 mi from the nearest point on a straight...
How many different ways can you make change for a quarter? (Different arrangements of the...
Seven balls are randomly withdrawn from an urn that contains 12 red, 16 blue, and...
Approximately 80,000 marriages took place in the state of New York last year. Estimate the...
The probability that a student passes the Probability and Statistics exam is 0.7. (i)Find the...
Customers at a gas station pay with a credit card (A), debit card (B), or...
It is conjectured that an impurity exists in 30% of all drinking wells in a...
Assume that the duration of human pregnancies can be described by a Normal model with...
According to a renowned expert, heavy smokers make up 70% of lung cancer patients. If...
Two cards are drawn successively and without replacement from an ordinary deck of playing cards...
Suppose that vehicles taking a particular freeway exit can turn right (R), turn left (L),...
A bag contains 6 red, 4 blue and 8 green marbles. How many marbles of...
A normal distribution has a mean of 50 and a standard deviation of 4. Please...
Seven women and nine men are on the faculty in the mathematics department at a...
An automatic machine in a manufacturing process is operating properly if the lengths of an...
Three cards are drawn without replacement from the 12 face cards (jacks, queens, and kings)...
Among 157 African-American men, the mean systolic blood pressure was 146 mm Hg with a...
A TIRE MANUFACTURER WANTS TO DETERMINE THE INNER DIAMETER OF A CERTAIN GRADE OF TIRE....
Differentiate the three measures of central tendency: ungrouped data.
Find the mean of the following data: 12,10,15,10,16,12,10,15,15,13
A wallet containing four P100 bills, two P200 bills, three P500 bills, and one P1,000...
The number of hours per week that the television is turned on is determined for...
Data was collected for 259 randomly selected 10 minute intervals. For each ten-minute interval, the...
Sixty-five randomly selected car salespersons were asked the number of cars they generally sell in...
A normal distribution has a mean of 80 and a standard deviation of 14. Determine...
True or false: a. All normal distributions are symmetrical b. All normal distributions have a...
Would you expect distributions of these variables to be uniform, unimodal, or bimodal? Symmetric or...
Annual sales, in millions of dollars, for 21 pharmaceutical companies follow. 8408 1374 1872 8879...
The velocity function (in meters per second) is given for a particle moving along a...
Find the area of the parallelogram with vertices A(-3,0) , B(-1,6) , C(8,5) and D(6,-1)
What is the area of the parallelogram with vertices A(-3, 0), B(-1, 5), C(7, 4),...
The integral represents the volume of a solid. Describe the solid. π∫01(y4−y8)dy a) The integral...
Two components of a minicomputer have the following joint pdf for their useful lifetimes X...
Use the table of values of f(x,y) to estimate the values of fx(3,2), fx(3,2.2), and...
Calculate net price factor and net price. Dollars list price −435.20$ Trade discount rate −26%,15%,5%.
Represent the line segment from P to Q by a vector-valued function and by a...
(x2+2xy−4y2)dx−(x2−8xy−4y2)dy=0
If f is continuous and integral 0 to 9 f(x)dx=4, find integral 0 to 3...
Find the parametric equation of the line through a parallel to ba=[3−4],b=[−78]
Find the velocity and position vectors of a particle that has the given acceleration and...
If we know that the f is continuous and integral 0 to 4f(x)dx=10, compute the...
Integration of (y⋅tanxy)
For the matrix A below, find a nonzero vector in the null space of A...
Find a nonzero vector orthogonal to the plane through the points P, Q, and R....
Suppose that the augmented matrix for a system of linear equations has been reduced by...
Find two unit vectors orthogonal to both (3 , 2, 1) and (- 1, 1,...
What is the area of the parallelogram whose vertices are listed? (0,0), (5,2), (6,4), (11,6)
Using T defined by T(x)=Ax, find a vector x whose image under T is b,...
Use the definition of Ax to write the matrix equation as a vector equation, or...
We need to find the volume of the parallelepiped with only one vertex at the...
List five vectors in Span {v1,v2}. For each vector, show the weights on v1 and...
(1) find the projection of u onto v and (2) find the vector component of...
Find the area of the parallelogram determined by the given vectors u and v. u...
(a) Find the point at which the given lines intersect. r = 2,...
(a) find the transition matrix from B toB′,(b) find the transition matrix fromB′to B,(c) verify...
A box contains 5 red and 5 blue marbles. Two marbles are withdrawn randomly. If...
Given the following vector X, find anon zero square marix A such that AX=0; You...
Construct a matrix whose column space contains (1, 1, 5) and (0, 3.1) and whose...
At what point on the paraboloid y=x2+z2 is the tangent plane parallel to the plane...
Label the following statements as being true or false. (a) If V is a vector...
Find the Euclidean distance between u and v and the cosine of the angle between...
Write an equation of the line that passes through (3, 1) and (0, 10)
There are 100 two-bedroom apartments in the apartment building Lynbrook West.. The montly profit (in...
State and prove the linearity property of the Laplace transform by using the definition of...
The analysis of shafts for a compressor is summarized by conformance to specifications. Suppose that...
The Munchies Cereal Company combines a number of components to create a cereal. Oats and...
Movement of a Pendulum A pendulum swings through an angle of 20∘ each second. If...
If sinx+siny=aandcosx+cosy=b then find tan(x−y2)
Find the values of x such that the angle between the vectors (2, 1, -1),...
Find the dimensions of the isosceles triangle of largest area that can be inscribed in...
Suppose that you are headed toward a plateau 50 meters high. If the angle of...
Airline passengers arrive randomly and independently at the passenger-screening facility at a major international airport....
Find an equation of the plane. The plane through the points (2, 1, 2), (3,...
Match each of the trigonometric expressions below with the equivalent non-trigonometric function from the following...
two small spheres spaced 20.0cm apart have equal charges. How many extra electrons must be...
The base of a pyramid covers an area of 13.0 acres (1 acre =43,560 ft2)...
Find out these functions' domain and range. To find the domain in each scenario, identify...
Your bank account pays an interest rate of 8 percent. You are considering buying a...
Whether f is a function from Z to R ifa)f(n)=±n.b)f(n)=n2+1.c)f(n)=1n2−4.
The probability density function of X, the lifetime of a certain type of electronic device...
A sandbag is released by a balloon that is rising vertically at a speed of...
A proton is located in a uniform electric field of2.75×103NCFind:a) the magnitude of the electric...
A rectangular plot of farmland are finite on one facet by a watercourse and on...
A solenoid is designed to produce a magnetic field of 0.0270 T at its center....
I want to find the volume of the solid enclosed by the paraboloidz=2+x2+(y−2)2and the planesz=1,x=−1y=0,andy=4
Let W be the subspace spanned by the u’s, and write y as the sum...
Can u find the point on the planex+2y+3z=13that is closest to the point (1,1,1). You...
A spring of negligible mass stretches 3.00 cm from its relaxed length when a force...
A force of 250 Newtons is applied to a hydraulic jack piston that is 0.01...
Three identical blocks connected by ideal strings are being pulled along a horizontal frictionless surface...
A credit card contains 16 digits between 0 and 9. However, only 100 million numbers...
Every real number is also a complex number? True of false?
Let F be a fixed 3x2 matrix, and let H be the set of all...
Find a vector a with representation given by the directed line segment AB. Draw AB...
Find A such that the given set is Col A. {[2s+3tr+s−2t4r+s3r−s−t]:r,s,t real}
Find the vector that has the same direction as (6, 2, -3) but is four...
For the matrices (a) find k such that Nul A is a subspace of Rk,...
How many subsets with an odd number of elements does a set with 10 elements...
In how many ways can a set of five letters be selected from the English...
Suppose that f(x) = x/8 for 3 < x < 5. Determine the following probabilities:...
Describe all solutions of Ax=0 in parametric vector form, where A is row equivalent to...
Find two vectors parallel to v of the given length. v=PQ→ with P(1,7,1) and Q(0,2,5);...
A dog in an open field runs 12.0 m east and then 28.0 m in...
Can two events with nonzero probabilities be both independent and mutually exclusive? Explain your reasoning.
Use the Intermediate Value Theorem to show that there is a root of the given...
In a fuel economy study, each of 3 race cars is tested using 5 different...
A company has 34 salespeople. A board member at the company asks for a list...
A dresser drawer contains one pair of socks with each of the following colors: blue,...
A restaurant offers a $12 dinner special with seven appetizer options, 12 choices for an...
A professor writes 40 discrete mathematics true/false questions. Of the statements in these questions, 17...
Suppose E(X)=5 and E[X(X–1)]=27.5, find ∈(x2) and the variance.
A Major League baseball diamond has four bases forming a square whose sides measure 90...
Express f(x)=4x3+6x2+7x+2 in term of Legendre Polynomials.
Find a basis for the space of 2×2 diagonal matrices. Basis ={[],[]}
Which of the following expressions are meaningful? Which are meaningless? Explain. a) (a⋅b)⋅c (a⋅b)⋅c has...
Vectors V1 and V2 are different vectors with lengths V1 and V2 respectively. Find the...
Find an equation for the plane containing the two (parallel) lines v1=(0,1,−2)+t(2,3,−1) and v2=(2,−1,0)+t(2,3,−1).
Find, correct to the nearest degree, the three angles of the triangle with the given...
Find the vector, not with determinants, but by using properties of cross products. (i+j)×(i−j)
Find the curve’s unit tangent vector. Also, find the length of the indicated portion of...
Construct a 4×3 matrix with rank 1
Find x such that the matrix is equal to its inverse.A=[7x−8−7]
Find a polynomial with integer coefficients that satisfies the given conditions. Q has degree 3...
Write in words how to read each of the following out loud.a.{x∈R′∣0<x<1}b.{x∈R∣x≤0orx⇒1}c.{n∈Z∣nisafactorof6}d.{n∈Z⋅∣nisafactorof6}
Pets Plus and Pet Planet are having a sale on the same aquarium. At Pets...
Find the average value of F(x, y, z) over the given region. F(x,y,z)=x2+9 over the...
Find the trace of the plane in the given coordinate plane. 3x−9y+4z=5,yz
Determine the level of measurement of the variable. Favorite color Choose the correct level of...
How wide is the chasm between what men and women earn in the workplace? According...
Write an algebraic expression for: 6 more than a number c.
Please, can u convert 3.16 (6 repeating) to a fraction.
Evaluate the expression. P(8, 3)
In a poker hand consisting of 5 cards, find the probability of holding 3 aces.
Give an expression that generates all angles coterminal with each angle. Let n represent any...
An ideal Otto cycle has a compression ratio of 10.5, takes in air at 90...
A piece of wire 10 m long is cut into two pieces. One piece is...
Put the following equation of a line into slope intercept form, simplifying all fractions 3x+3y=24
Find the point on the hyperbola xy = 8 that is closest to the point...
Water is pumped from a lower reservoir to a higher reservoir by a pump that...
A piston–cylinder device initially contains 0.07m3 of nitrogen gas at 130 kPa and 180∘. The...
Write an algebraic expression for each word phrase. 4 more than p
A club has 25 members. a) How many ways are there to choose four members...
For each of the sets below, determine whether {2} is an element of that set....
Which expression has both 8 and n as factors?
If repetitions are not permitted (a) how many 3 digit number can be formed from...
To determine the sum of all multiples of 3 between 1 and 1000
On average, there are 3 accidents per month at one intersection. We need to find...
One number is 2 more than 3 times another. Their sum is 22. Find the...
The PMF for a flash drive with X (GB) of memory that was purchased is...
An airplane needs to reach a velocity of 203.0 km/h to takeoff. On a 2000...
A racquetball strikes a wall with a speed of 30 m/s and rebounds with a...
Assuming that the random variable x has a cumulative distribution function,F(x)={0,x<00.25x,0≤x<51,5≤xDetermine the following:a)p(x<2.8)b)p(x>1.5)c)p(x<−z)d)p(x>b)
At t = 0 a grinding wheel has an angular velocity of 24.0 rad/s. It...
How many 3/4's are in 1?
You’re driving down the highway late one night at 20 m/s when a deer steps...
Table salt contains 39.33 g of sodium per 100 g of salt. The U.S. Food...
The constant-pressure heat capacity of a sample of a perfect gas was found to vary...
Coffee is draining from a conical filter into a cylindrical coffepot at the rate of...
Cart is driven by a large propeller or fan, which can accelerate or decelerate the...
A vending machine dispenses coffee into an eight-ounce cup. The amounts of coffee dispensed into...
On an essentially frictionless, horizontal ice rink, a skater moving at 3.0 m/s encounters a...
The gage pressure in a liquid at a depth of 3 m is read to...
Consider a cylindrical specimen of a steel alloy 8.5 mm (0.33 in.) in diameter and...
Calculate the total kinetic energy, in Btu, of an object with a mass of 10...
A 0.500-kg mass on a spring has velocity as a function of time given by...
An Australian emu is running due north in a straight line at a speed of...
Another pitfall cited is expecting to improve the overall performance of a computer by improving...
You throw a glob of putty straight up toward the ceiling, which is 3.60 m...
A 0.150-kg frame, when suspended from a coil spring, stretches the spring 0.070 m. A...
A batch of 140 semiconductor chips is inspected by choosing a sample of 5 chips....
A rock climber stands on top of a 50-m-high cliff overhanging a pool of water....
A tank whose bottom is a mirror is filled with water to a depth of...
Two sites are being considered for wind power generation. In the first site, the wind...
0.250 kilogram of water at75.0∘Care contained in a tiny, inert beaker. How much ice, at...
Two boats start together and race across a 60-km-wide lake and back. Boat A goes...
A roller coaster moves 200 ft horizontally and the rises 135 ft at an angle...
A tow truck drags a stalled car along a road. The chain makes an angle...
Consider the curve created by2x2+3y2–4xy=36(a) Show thatdydx=2y−2x3y−2x(b) Calculate the slope of the line perpendicular to...
The current entering the positive terminal of a device is i(t)=6e−2t mA and the voltage...
The fastest measured pitched baseball left the pitcher’s hand at a speed of 45.0 m/s....
Calculate the total potential energy, in Btu, of an object that is 20 ft below...
A chemist in an imaginary universe, where electrons have a different charge than they do...
When jumping, a flea reaches a takeoff speed of 1.0 m/s over a distance of...
Determine the energy required to accelerate a 1300-kg car from 10 to 60 km/h on...
The deepest point in the ocean is 11 km below sea level, deeper than MT....
A golfer imparts a speed of 30.3 m/s to a ball, and it travels the...
Calculate the frequency of each of the following wavelengths of electromagnetic radiation. A) 632.8 nm...
Prove that there is a positive integer that equals the sum of the positive integers...
A hurricane wind blows across a 6.00 m×15.0 m flat roof at a speed of...
If an electron and a proton are expelled at the same time,2.0×10−10mapart (a typical atomic...
The speed of sound in air at 20 C is 344 m/s. (a) What is...
Which of the following functions f has a removable discontinuity at a? If the discontinuity...
A uniform steel bar swings from a pivot at one end with a period of...
A wind farm generator uses a two-bladed propellermounted on a pylon at a height of...
A copper calorimeter can with mass 0.100 kg contains 0.160 kgof water and 0.018 kg...
Jones figures that the total number of thousands of miles that a used auto can...
Assign a binary code in some orderly manner to the 52 playingcards. Use the minimum...
A copper pot with mass 0.500 kg contains 0.170 kg of water ata temperature of...
Ea for a certain biological reaction is 50 kJ/mol, by what factor ( how many...
When a person stands on tiptoe (a strenuous position), the position of the foot is...
A solution was prepared by dissolving 1210 mg of K3Fe(CN)6 (329.2 g/mol) in sufficient waterto...
A 58-kg skier is going down a slope oriented 35 degree abovethe horizontal. The area...
The mechanics at lincoln automotive are reboring a 6-in deepcylinder to fit a new piston....
A 0.48 kg piece of wood floats in water but is found to sinkin alcohol...
A 50-g ice cube at 0oC is heated until 45-g hasbecome water at 100oC and...
A solution containing 6.23 ppm of KMnO4 had a transmittance of 0.195 in a 1.00-cm...
A black body at 7500K consists of an opening of diameter 0.0500mm, looking into an...
A new absolute temperature scale is proposed. On thisscale the ice point of water is...
A 65.0 mm focal length converging lens is 78.0 mm away from a sharp image....
A crate of fruit with mass 35.0 kg and specific heat capacity 3650 J/Kg ....
A freezer has a thermal efficiency of 2.40. Thefreezer is to convert 1.80 kg of...
A horizontal force of 210N is exerted on a 2.0 kg discus as it rotates...
Lead has a specific heat of 0.030 cal/gC. In an insulated container, 300 grams of...
A parachutist relies on air resistance mainly on her parachute to decrease her downward velocity....
The distance between a carbon atom (m=12 u) and an oxygen atom (m + 16...
A car heading north collides at an intersection with a truckheading east. If they lock...
Water stands at a depth H in a large, open tank whose sidewalls are vertical....
The heaviest invertebrate is the giant squid, which is estimated to have a weight of...
Which of the following is a correct comment? */ Comments */ ** Comment ** /*...
The concentrated sulfuric acid we use in the laboratory is 98% H2SO4 by mass. Calculate...
Consider the reaction N2(g)+3H2(g)→2NH3(g) suppose that a particular moment during the reaction molecular hydrogen on...
use Green’s Theorem to find the counterclockwise circulation and outward flux for the field F...
- High School Questions
- College Questions
- Math Solver
- Top Questions 2
- Term of Service
- Payment Policy
Connect with us
Get Plainmath App
- Google Play
E-mail us: [email protected]
Our Service is useful for:
Plainmath is a platform aimed to help users to understand how to solve math problems by providing accumulated knowledge on different topics and accessible examples.
2023 Plainmath. All rights reserved

13 World’s Hardest Math Problems | With Solutions

For decades, mathematics has been a fascinating and challenging topic. People have been interested in learning and getting good at math from ancient Greeks to modern mathematicians. But have you ever wondered which math problem is the most challenging?
What could be so tricky and complicated that only some of the brightest mathematicians have been able to solve it? This article will look at 13 of the hardest math problems and how mathematicians have tried to solve them.
Continue reading the article to explore the world’s hardest math problems, listed below.
The Poincaré Conjecture
The prime number theorem, fermat’s last theorem, the reimann hypothesis, classification of finite simple groups, four color theorem, goldbach’s conjecture.
- Inscribed Square Problem
Twin Prime Conjecture
The continuum hypothesis, collatz conjecture, birch and swinnerton-dyer conjecture, the kissing number problem.
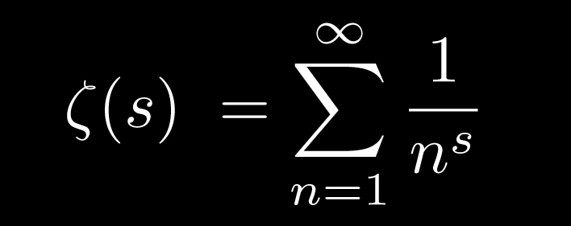
Mathematicians struggled for about a century with the Poincaré conjecture, which was put forth by Henri Poincaré in 1904.
According to this theory,
every closed, connected three-dimensional space is topologically identical to a three-dimensional sphere (S3).
We must explore the field of topology to comprehend what this entails. The study of properties of objects that hold after being stretched, bent, or otherwise distorted is known as topology. In other words, topologists are fascinated by how things can change without rupturing or being torn.
The topology of three-dimensional spaces is the subject of the Poincaré conjecture. A space volume with three dimensions—length, breadth, and height—is a three-dimensional space. A three-dimensional object called a sphere has a round and curved surface.
According to the Poincaré Conjecture, a three-sphere (S3), or the collection of points in four dimensions that are all at a fixed distance from a given point, is topologically identical to every simply-connected, closed, three-dimensional space (i.e., one that has no gaps or voids) and edges.
Although it would appear easy, it took more than a century to confirm the conjecture thoroughly.
- Poincaré expanded his hypothesis to include any dimension (n-sphere).
- Stephen Smale, an American mathematician, proved the conjecture to be true for n = 5 in 1961.
- Freedman, another American mathematician, proved the conjecture to be true for n = 4 in 1983.
- Grigori Perelman, a Russian mathematician, then proved the conjecture to be true for n = 3 in 2002, completing the solution.
- Perelman eventually addressed the problem by combining topology and geometry. One of the highest awards in mathematics, the Fields Medal, was given to all three mathematicians. Perelman rejected the Fields Medal. He was also given a $1 million prize by the Clay Mathematics Institute (CMI) of Cambridge, Massachusetts, for resolving one of the seven Millennium Problems, considered one of the world’s most challenging mathematical puzzles. However, he turned it down as well.
The prime number theorem (PNT) explains how prime numbers asymptotically distribute among positive integers. It shows how fast primes become less common as numbers get bigger.
The prime number theorem states that the number of primes below a given natural number N is roughly N/log(N), with the word “approximately” carrying the typical statistical connotations.
- Two mathematicians, Jacques Hadamard and Charles Jean de la Vallée Poussin, independently proved the Prime Number Theorem in 1896. Since then, the proof has frequently been the subject of rewrites, receiving numerous updates and simplifications. However, the theorem’s influence has only increased.
French lawyer and mathematician Pierre de Fermat lived in the 17th century. Fermat was one of the best mathematicians in history. He talked about many of his theorems in everyday conversation because math was more of a hobby for him.
He made claims without proof, leaving it to other mathematicians decades or even centuries later to prove them. The hardest of them is now referred to as Fermat’s Last Theorem.
Fermat’s last theorem states that;
there are no positive integers a, b, and c that satisfy the equation an + bn = cn for any integer value of n greater than 2.
- In 1993, British mathematician Sir Andrew Wiles solved one of history’s longest mysteries. As a result of his efforts, Wiles was knighted by Queen Elizabeth II and given a special honorary plaque rather than the Fields Medal because he was old enough to qualify.
- Wiles synthesized recent findings from many distinct mathematics disciplines to find answers to Fermat’s well-known number theory query.
- Many people think Fermat never had proof of his Last Theorem because Elliptic Curves were utterly unknown in Fermat’s time.
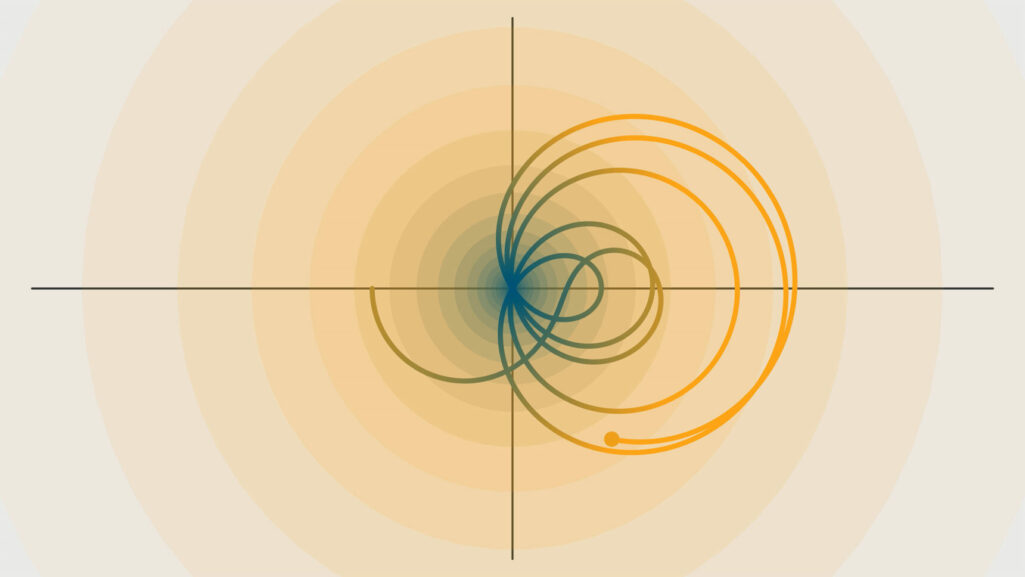
Mathematicians have been baffled by the Riemann Hypothesis for more than 150 years. It was put forth by the German mathematician Bernhard Riemann in 1859. According to Riemann’s Hypothesis
Every Riemann zeta function nontrivial zero has a real component of ½.
The distribution of prime numbers can be described using the Riemann zeta function. Prime numbers, such as 2, 3, 5, 7, and 11, can only be divided by themselves and by one. Mathematicians have long been fascinated by the distribution of prime numbers because figuring out their patterns and relationships can provide fresh perspectives on number theory and other subject areas.
Riemann’s hypothesis says there is a link between how prime numbers are spread out and how the zeros of the Riemann zeta function are set up. If this relationship is accurate, it could significantly impact number theory and help us understand other parts of mathematics in new ways.
- The Riemann Hypothesis is still unproven, despite being one of mathematics’ most significant unsolved issues.
- Michael Atiyah, a mathematician, proclaimed in 2002 that he had proved the Riemann Hypothesis, although the mathematical community still needs to acknowledge his claim formally.
- The Clay Institute has assigned the hypothesis as one of the seven Millennium Prize Problems. A $1 million prize is up for anyone who can prove the Riemann hypothesis to be true or false.
Abstract algebra can be used to do many different things, like solve the Rubik’s cube or show a body-swapping fact in Futurama. Algebraic groups follow a few basic rules, like having an “identity element” that adds up to 0. Groups can be infinite or finite, and depending on your choice of n, it can be challenging to describe what a group of a particular size n looks like.
There is one possible way that the group can look at whether n is 2 or 3. There are two possibilities when n equals 4. Mathematicians intuitively wanted a complete list of all feasible groups for each given size.
- The categorization of finite simple groups, arguably the most significant mathematical undertaking of the 20th century, was planned by Harvard mathematician Daniel Gorenstein, who presented the incredibly intricate scheme in 1972.
- By 1985, the project was almost finished, but it had consumed so many pages and publications that peer review by a single person was impossible. The proof’s numerous components were eventually reviewed one by one, and the classification’s completeness was verified.
- The proof was acknowledged mainly by the 1990s. Verification was later streamlined to make it more manageable, and that project is still active today.

According to four color theorem
Any map in a plane can be given a four-color coloring utilizing the rule that no two regions sharing a border (aside from a single point) should have the same color.
- Two mathematicians at the University of Illinois at Urbana-Champaign, Kenneth Appel and Wolfgang Hakan identified a vast, finite number of examples to simplify the proof. They thoroughly examined the over 2,000 cases with the aid of computers, arriving at an unheard-of proof style.
- The proof by Appel and Hakan was initially debatable because a computer generated it, but most mathematicians ultimately accepted it. Since then, there has been a noticeable increase in the usage of computer-verified components in proofs, as Appel and Hakan set the standard.
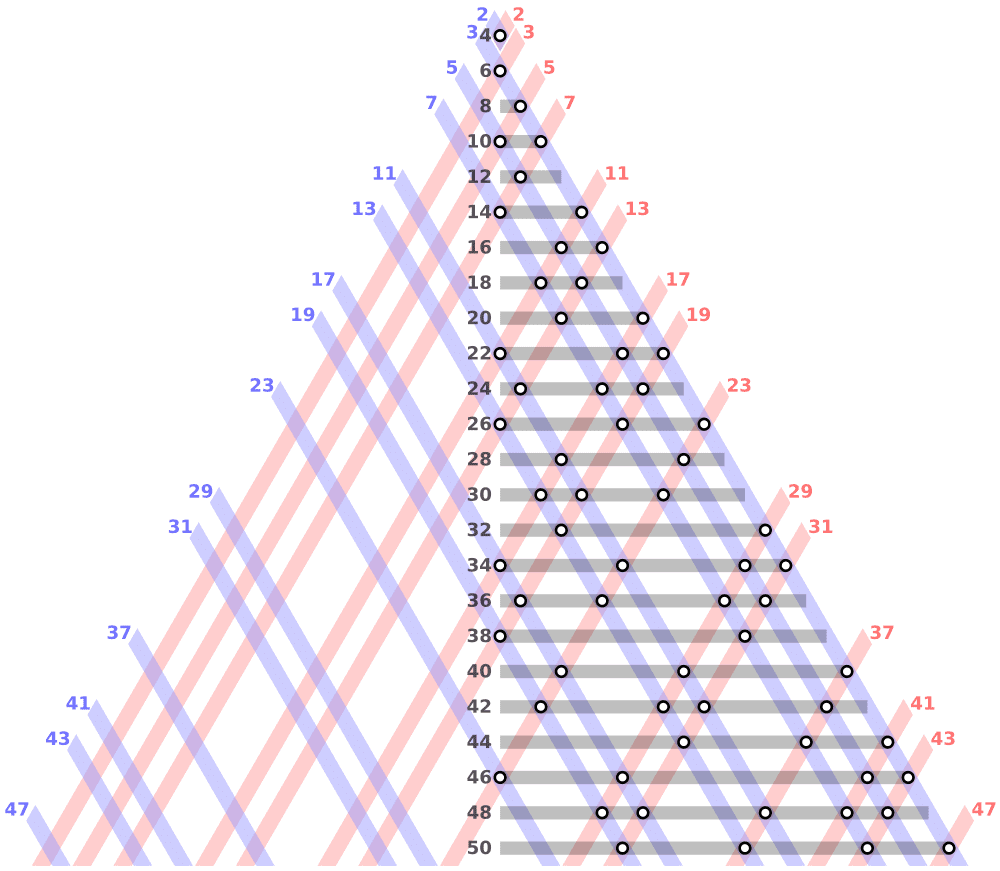
According to Goldbach’s conjecture, every even number (higher than two) is the sum of two primes. You mentally double-check the following for small numbers: 18 is 13 + 5, and 42 is 23 + 19. Computers have tested the conjecture for numbers up to a certain magnitude. But for all natural numbers, we need proof.
Goldbach’s conjecture resulted from correspondence between Swiss mathematician Leonhard Euler and German mathematician Christian Goldbach in 1742.
- Euler is regarded as one of the finest mathematicians in history. Although I cannot prove it, in the words of Euler, “I regard [it] as a totally certain theorem.”
- Euler might have understood why it is conversely tricky to resolve this problem. More significant numbers have more methods than smaller ones to be expressed as sums of primes. In the same way that only 3+5 can split eight into two prime numbers, 42 can be divided into 5+37, 11+31, 13+29, and 19+23. Therefore, for vast numbers, Goldbach’s Conjecture is an understatement.
- The Goldbach conjecture has been confirmed for all integers up to 4*1018, but an analytical proof has yet to be found.
- Many talented mathematicians have attempted to prove it but have yet to succeed.
Inscribed Sq uare Problem
Another complex geometric puzzle is the “square peg problem,” also known as the “inscribed square problem” or the “Toeplitz conjecture.” The Inscribe Square Problem Hypothesis asks:
Does every simple closed curve have an inscribed square?
In other words, it states, ” For any curve, you could draw on a flat page whose ends meet (closed), but lines never cross (simple); we can fit a square whose four corners touch the curve somewhere.
- The inscribed square problem is unsolved in geometry.
- It bears the names of mathematicians Bryan John Birch and Peter Swinnerton-Dyer, who established the conjecture using automated calculation in the first half of the 1960s.
- Only specific instances of the hypothesis have been proven as of 2023.
The Twin Prime Conjecture is one of many prime number-related number theory puzzles. Twin primes are two primes that differ from each other by two. The twin prime examples include 11 and 13 and 599 and 601. Given that there are an unlimited number of prime numbers, according to number theory, there should also be an endless number of twin primes.
The Twin Prime Conjecture asserts that there are limitless numbers of twin primes.
- In 2013, Yitang Zhang did groundbreaking work to solve the twin prime conjecture.
- However, the twin prime conjecture still needs to be solved.
Infinities are everywhere across modern mathematics. There are infinite positive whole numbers (1, 2, 3, 4, etc.) and infinite lines, triangles, spheres, cubes, polygons, etc. It has also been proven by modern mathematics that there are many sizes of infinity.
If the elements of a set can be arranged in a 1-to-1 correspondence with the positive whole numbers, we say the set of elements is countably infinite. Therefore, the set of whole numbers and rational numbers are countable infinities.
Georg Cantor found that the set of real numbers is uncountable. In other words, even if we used all the whole numbers, we would never be able to go through and provide a positive whole number to every real number. Uncountable infinities might be seen as “larger” than countable infinities.
- According to the continuum hypothesis, there must be a set of numbers whose magnitude strictly falls between countably infinite and uncountably infinite. The continuum hypothesis differs from the other problems in this list in that it is impossible to solve or at least impossible to address using present mathematical methods.
- As a result, even though we have yet to determine whether the continuum hypothesis is accurate, we do know that it cannot be supported by the tools of modern set theory either. It would be necessary to develop a new framework for set theory, which has yet to be done, to resolve the continuum hypothesis.
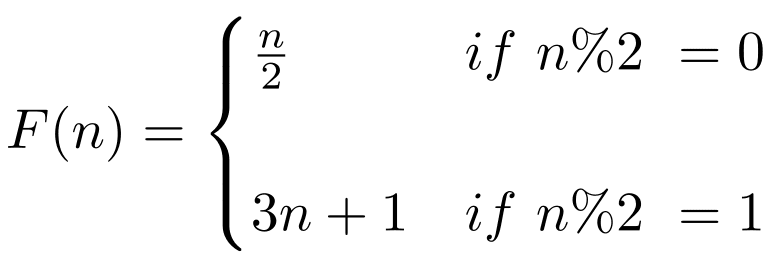
To understand Collatz’s conjecture, try to understand the following example. First, you have to pick a positive number, n. Then, from the last number, create the following sequence:
If the number is even, divide by 2. If it’s odd, multiply by 3 and then add 1. The objective is to keep going through this sequence until you reach 1. Let’s try this sequence with the number 12 as an example. Starting with number 12, we get: 12, 6, 3, 10, 5, 16, 8, 4, 2, 1
Starting at 19, we obtain the following: 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1
According to the Collatz conjecture, this sequence will always end in 1, regardless of the value of n you started with. This speculation has been tested for all values of n up to 87,260, but no proof has been found.
- Collatz’s conjecture has been unsolved up till now.
- Mathematical problem-solver Paul Erdree once said of the Collatz Conjecture, “Mathematics may not be ready for such problems.”
Two British mathematicians, Bryan Birch and Peter Swinnerton-Dyer formulated their hypotheses in the 1960s. The Birch and Swinnerton-Dyer conjecture in mathematics describes rational answers to the equations defining an elliptic curve.
This hypothesis states explicitly that there are an infinite number of rational points (solutions) if ζ(1) equals 0 and that there are only a finite number of such places if ζ(1) is not equal to 0.
- For Birch and Swinnerton-Dyer’s conjecture, Euclid provided a comprehensive solution, but this becomes very challenging for problems with more complex solutions.
- Yu. V. Matiyasevich demonstrated in 1970 that Hilbert’s tenth problem could not be solved, saying there is no mechanism for identifying when such equations have a whole number solution.
- As of 2023, only a few cases have been solved.

Each sphere has a Kissing Number, the number of other spheres it is kissing, when a group of spheres is packed together in one area. For example, your kissing number is six if you touch six nearby spheres. Nothing difficult.
Mathematically, the condition can be described by the average kissing number of a tightly packed group of spheres. However, a fundamental query regarding the kissing number remains unsolved.
First, you must learn about dimensions to understand the kissing number problem. In mathematics, dimensions have a special meaning as independent coordinate axes. The two dimensions of a coordinate plane are represented by the x- and y-axes.
A line is a two-dimensional object, whereas a plane is a three-dimensional object. Mathematicians have established the highest possible kissing number for spheres with those few dimensions for these low numbers. On a 1-D line, there are two spheres—one to your left and the other to your right.
- The Kissing Problem is generally unsolved in dimensions beyond three.
- A complete solution for the kissing problem number faces many obstacles, including computational constraints. The debate continued to solve this problem.
The Bottom Line
When it comes to pushing the boundaries of the enormous human ability to comprehend and problem-solving skills, the world’s hardest math problems are unquestionably the best. These issues, which range from the evasive Continuum Hypothesis to the perplexing Riemann Hypothesis, continue to puzzle even the sharpest mathematicians.
But regardless of how challenging they are, these problems keep mathematicians inspired and driven to explore new frontiers. Whether or not these problems ever get resolved, they illustrate the enormous ability of the human intellect.
Even though some of these issues might never fully be resolved, they continue to motivate and inspire advancement within the field of mathematics and reflects how broad and enigmatic this subject is!
Let us know out of these 13 problems which problem you find the hardest!
Related Posts

I want to be prodigy genius?
- Skip to main content
- Skip to primary sidebar
- Skip to footer
Additional menu
Khan Academy Blog
Free Math Worksheets — Over 100k free practice problems on Khan Academy
Looking for free math worksheets.
You’ve found something even better!
That’s because Khan Academy has over 100,000 free practice questions. And they’re even better than traditional math worksheets – more instantaneous, more interactive, and more fun!
Just choose your grade level or topic to get access to 100% free practice questions:
Kindergarten, basic geometry, pre-algebra, algebra basics, high school geometry.
- Trigonometry
Statistics and probability
High school statistics, ap®︎/college statistics, precalculus, differential calculus, integral calculus, ap®︎/college calculus ab, ap®︎/college calculus bc, multivariable calculus, differential equations, linear algebra.
- Addition and subtraction
- Place value (tens and hundreds)
- Addition and subtraction within 20
- Addition and subtraction within 100
- Addition and subtraction within 1000
- Measurement and data
- Counting and place value
- Measurement and geometry
- Place value
- Measurement, data, and geometry
- Add and subtract within 20
- Add and subtract within 100
- Add and subtract within 1,000
- Money and time
- Measurement
- Intro to multiplication
- 1-digit multiplication
- Addition, subtraction, and estimation
- Intro to division
- Understand fractions
- Equivalent fractions and comparing fractions
- More with multiplication and division
- Arithmetic patterns and problem solving
- Quadrilaterals
- Represent and interpret data
- Multiply by 1-digit numbers
- Multiply by 2-digit numbers
- Factors, multiples and patterns
- Add and subtract fractions
- Multiply fractions
- Understand decimals
- Plane figures
- Measuring angles
- Area and perimeter
- Units of measurement
- Decimal place value
- Add decimals
- Subtract decimals
- Multi-digit multiplication and division
- Divide fractions
- Multiply decimals
- Divide decimals
- Powers of ten
- Coordinate plane
- Algebraic thinking
- Converting units of measure
- Properties of shapes
- Ratios, rates, & percentages
- Arithmetic operations
- Negative numbers
- Properties of numbers
- Variables & expressions
- Equations & inequalities introduction
- Data and statistics
- Negative numbers: addition and subtraction
- Negative numbers: multiplication and division
- Fractions, decimals, & percentages
- Rates & proportional relationships
- Expressions, equations, & inequalities
- Numbers and operations
- Solving equations with one unknown
- Linear equations and functions
- Systems of equations
- Geometric transformations
- Data and modeling
- Volume and surface area
- Pythagorean theorem
- Transformations, congruence, and similarity
- Arithmetic properties
- Factors and multiples
- Reading and interpreting data
- Negative numbers and coordinate plane
- Ratios, rates, proportions
- Equations, expressions, and inequalities
- Exponents, radicals, and scientific notation
- Foundations
- Algebraic expressions
- Linear equations and inequalities
- Graphing lines and slope
- Expressions with exponents
- Quadratics and polynomials
- Equations and geometry
- Algebra foundations
- Solving equations & inequalities
- Working with units
- Linear equations & graphs
- Forms of linear equations
- Inequalities (systems & graphs)
- Absolute value & piecewise functions
- Exponents & radicals
- Exponential growth & decay
- Quadratics: Multiplying & factoring
- Quadratic functions & equations
- Irrational numbers
- Performing transformations
- Transformation properties and proofs
- Right triangles & trigonometry
- Non-right triangles & trigonometry (Advanced)
- Analytic geometry
- Conic sections
- Solid geometry
- Polynomial arithmetic
- Complex numbers
- Polynomial factorization
- Polynomial division
- Polynomial graphs
- Rational exponents and radicals
- Exponential models
- Transformations of functions
- Rational functions
- Trigonometric functions
- Non-right triangles & trigonometry
- Trigonometric equations and identities
- Analyzing categorical data
- Displaying and comparing quantitative data
- Summarizing quantitative data
- Modeling data distributions
- Exploring bivariate numerical data
- Study design
- Probability
- Counting, permutations, and combinations
- Random variables
- Sampling distributions
- Confidence intervals
- Significance tests (hypothesis testing)
- Two-sample inference for the difference between groups
- Inference for categorical data (chi-square tests)
- Advanced regression (inference and transforming)
- Analysis of variance (ANOVA)
- Scatterplots
- Data distributions
- Two-way tables
- Binomial probability
- Normal distributions
- Displaying and describing quantitative data
- Inference comparing two groups or populations
- Chi-square tests for categorical data
- More on regression
- Prepare for the 2020 AP®︎ Statistics Exam
- AP®︎ Statistics Standards mappings
- Polynomials
- Composite functions
- Probability and combinatorics
- Limits and continuity
- Derivatives: definition and basic rules
- Derivatives: chain rule and other advanced topics
- Applications of derivatives
- Analyzing functions
- Parametric equations, polar coordinates, and vector-valued functions
- Applications of integrals
- Differentiation: definition and basic derivative rules
- Differentiation: composite, implicit, and inverse functions
- Contextual applications of differentiation
- Applying derivatives to analyze functions
- Integration and accumulation of change
- Applications of integration
- AP Calculus AB solved free response questions from past exams
- AP®︎ Calculus AB Standards mappings
- Infinite sequences and series
- AP Calculus BC solved exams
- AP®︎ Calculus BC Standards mappings
- Integrals review
- Integration techniques
- Thinking about multivariable functions
- Derivatives of multivariable functions
- Applications of multivariable derivatives
- Integrating multivariable functions
- Green’s, Stokes’, and the divergence theorems
- First order differential equations
- Second order linear equations
- Laplace transform
- Vectors and spaces
- Matrix transformations
- Alternate coordinate systems (bases)
Frequently Asked Questions about Khan Academy and Math Worksheets
Why is khan academy even better than traditional math worksheets.
Khan Academy’s 100,000+ free practice questions give instant feedback, don’t need to be graded, and don’t require a printer.
| Math Worksheets | Khan Academy |
|---|---|
| Math worksheets take forever to hunt down across the internet | Khan Academy is your one-stop-shop for practice from arithmetic to calculus |
| Math worksheets can vary in quality from site to site | Every Khan Academy question was written by a math expert with a strong education background |
| Math worksheets can have ads or cost money | Khan Academy is a nonprofit whose resources are always free to teachers and learners – no ads, no subscriptions |
| Printing math worksheets use up a significant amount of paper and are hard to distribute during virtual learning | Khan Academy practice requires no paper and can be distributed whether your students are in-person or online |
| Math worksheets can lead to cheating or a lack of differentiation since every student works on the same questions | Khan Academy has a full question bank to draw from, ensuring that each student works on different questions – and at their perfect skill level |
| Math worksheets can slow down student learning since they need to wait for feedback | Khan Academy gives instant feedback after every answer – including hints and video support if students are stuck |
| Math worksheets take up time to collect and take up valuable planning time to grade | Khan Academy questions are graded instantly and automatically for you |
What do Khan Academy’s interactive math worksheets look like?
Here’s an example:
What are teachers saying about Khan Academy’s interactive math worksheets?
“My students love Khan Academy because they can immediately learn from their mistakes, unlike traditional worksheets.”
Is Khan Academy free?
Khan Academy’s practice questions are 100% free—with no ads or subscriptions.
What do Khan Academy’s interactive math worksheets cover?
Our 100,000+ practice questions cover every math topic from arithmetic to calculus, as well as ELA, Science, Social Studies, and more.
Is Khan Academy a company?
Khan Academy is a nonprofit with a mission to provide a free, world-class education to anyone, anywhere.
Want to get even more out of Khan Academy?
Then be sure to check out our teacher tools . They’ll help you assign the perfect practice for each student from our full math curriculum and track your students’ progress across the year. Plus, they’re also 100% free — with no subscriptions and no ads.
Get Khanmigo
The best way to learn and teach with AI is here. Ace the school year with our AI-powered guide, Khanmigo.
For learners For teachers For parents

Choose Your Test
- Search Blogs By Category
- College Admissions
- AP and IB Exams
- GPA and Coursework
The 15 Hardest SAT Math Questions Ever

Want to test yourself against the most difficult SAT math questions? Want to know what makes these questions so difficult and how best to solve them? If you're ready to really sink your teeth into the SAT math section and have your sights set on that perfect score, then this is the guide for you.
We've put together what we believe to be the 15 most difficult questions for the current Digital SAT , with strategies and answer explanations for each. These are all hard SAT Math questions from College Board SAT practice tests, which means understanding them is one of the best ways to study for those of you aiming for perfection.
Image: Sonia Sevilla /Wikimedia
Brief Overview of SAT Math
There are two sections on the SAT: SAT Reading and Writing and SAT Math . Both sections are divided into two modules, and SAT Reading and Writing always comes first. So, the S AT Math modules will be the 3rd and 4th modules you’ll see on test day. Both math modules allow you to use a calculator.
Each math module is arranged in order of ascending difficulty (where the longer it takes to solve a problem and the fewer people who answer it correctly, the more difficult it is). On each module, question 1 will be "easy" and question 22 will be considered "difficult." The modules are made up of both multiple choice and grid-in questions , and there isn’t a particular order for grid-ins—they can come anywhere in the module and be of any difficulty. 75% of SAT Math questions are multiple choice and 25% are grid-ins.
With very few exceptions, then, the most difficult SAT math problems will be clustered at the end of each module. In addition to their placement on the test, though, these questions also share a few other commonalities. In a minute, we'll look at example questions and how to solve them, then analyze them to figure out what these types of questions have in common.
But First: Should You Be Focusing on the Hardest Math Questions Right Now?
If you're just getting started in your study prep (or if you've simply skipped this first, crucial step), definitely stop and take a full practice test to gauge your current scoring level. Check out our guide to all the free SAT practice tests available online and then sit down to take a test all at once.
The absolute best way to assess your current level is to simply take the SAT practice test as if it were real , keeping strict timing and working straight through with only the allowed breaks (we know—probably not your favorite way to spend a Saturday). Once you've got a good idea of your current level and percentile ranking, you can set milestones and goals for your ultimate SAT Math score.
If you're currently scoring in the 200-400 or the 400-600 range on SAT Math, your best bet is first to check out our guide to improving your math score to be consistently at or over a 600 before you start in trying to tackle the most difficult math problems on the test.
If, however, you're already scoring above a 600 on the Math section and want to test your mettle for the real SAT, then definitely proceed to the rest of this guide. If you're aiming for perfect (or close to) , then you'll need to know what the most difficult SAT math questions look like and how to solve them. And luckily, that's exactly what we'll do.
There are a limited number of official SAT practice tests, especially now that the SAT has gone completely digital. We recommend beginning with the six official, digital SAT practice tests available through College Board’s Bluebook software. If you’ve finished those and want even more prep, though, there are lots of older (but still officially produced by the College Board) tests you can use. Most of the questions below are from these practice tests, so if you’re worried about spoiling those tests, stop reading this guide now and come back when you’ve completed all the older official practice tests.

Now let's get to our list of questions (whoo)!
Image: Niytx /DeviantArt
The 15 Hardest SAT Math Questions
Now that you're sure you should be attempting these questions, let's dive right in! We've curated 15 of the most difficult SAT Math questions for you to try below, along with walkthroughs of how to get the answer (if you're stumped).
The equation above shows how temperature F, measured in degrees Fahrenheit, relates to a temperature C, measured in degrees Celsius. Based on the equation, which of the following must be true?
- A temperature increase of 1 degree Fahrenheit is equivalent to a temperature increase of 59 degree Celsius.
- A temperature increase of 1 degree Celsius is equivalent to a temperature increase of 1.8 degrees Fahrenheit.
- A temperature increase of 59 degree Fahrenheit is equivalent to a temperature increase of 1 degree Celsius.
A) I only B) II only C) III only D) I and II only
ANSWER EXPLANATION: Think of the equation as an equation for a line
where in this case
C=59F−59(32)
You can see the slope of the graph is 59, which means that for an increase of 1 degree Fahrenheit, the increase is 59 of 1 degree Celsius.
Therefore, statement I is true. This is the equivalent to saying that an increase of 1 degree Celsius is equal to an increase of 95 degrees Fahrenheit.
Since 95 = 1.8, statement II is true.
The only answer that has both statement I and statement II as true is D , but if you have time and want to be absolutely thorough, you can also check to see if statement III (an increase of 59 degree Fahrenheit is equal to a temperature increase of 1 degree Celsius) is true:
C=2581(whichis≠1)
An increase of 59 degree Fahrenheit leads to an increase of 2581, not 1 degree, Celsius, and so Statement III is not true.
The final answer is D.
The equation 24x2+25x−47ax−2=−8x−3−53ax−2 is true for all values of x≠2a, where a is a constant.
What is the value of a?
A) -16 B) -3 C) 3 D) 16
ANSWER EXPLANATION: There are two ways to solve this question. The faster way is to multiply each side of the given equation by ax−2 (so you can get rid of the fraction). When you multiply each side by ax−2, you should have:
24x2+25x−47=(−8x−3)(ax−2)−53
You should then multiply (−8x−3) and (ax−2) using FOIL.
24x2+25x−47=−8ax2−3ax+16x+6−53
Then, reduce on the right side of the equation
24x2+25x−47=−8ax2−3ax+16x−47
Since the coefficients of the x2-term have to be equal on both sides of the equation, −8a=24, or a=−3.
The other option which is longer and more tedious is to attempt to plug in all of the answer choices for a and see which answer choice makes both sides of the equation equal. Again, this is the longer option, and I do not recommend it for the actual SAT as it will waste too much time.
The final answer is B.
If 3x−y=12, what is the value of 8x2y?
A) 212 B) 44 C) 82 D) The value cannot be determined from the information given.
ANSWER EXPLANATION: One approach is to express
so that the numerator and denominator are expressed with the same base. Since 2 and 8 are both powers of 2, substituting 23 for 8 in the numerator of 8x2y gives
which can be rewritten
Since the numerator and denominator of have a common base, this expression can be rewritten as 2(3x−y). In the question, it states that 3x−y=12, so one can substitute 12 for the exponent, 3x−y, which means that
The final answer is A.
Points A and B lie on a circle with radius 1, and arc AB⌢ has a length of π3. What fraction of the circumference of the circle is the length of arc AB⌢?
ANSWER EXPLANATION: To figure out the answer to this question, you'll first need to know the formula for finding the circumference of a circle.
The circumference, C, of a circle is C=2πr, where r is the radius of the circle. For the given circle with a radius of 1, the circumference is C=2(π)(1), or C=2π.
To find what fraction of the circumference the length of AB⌢ is, divide the length of the arc by the circumference, which gives π3÷2π. This division can be represented by π3*12π=16.
The fraction 16 can also be rewritten as 0.166 or 0.167.
The final answer is 16, 0.166, or 0.167.
If the expression above is rewritten in the form a+bi, where a and b are real numbers, what is the value of a? (Note: i=−1)
ANSWER EXPLANATION: To rewrite 8−i3−2i in the standard form a+bi, you need to multiply the numerator and denominator of 8−i3−2i by the conjugate, 3+2i. This equals
(8−i3−2i)(3+2i3+2i)=24+16i−3+(−i)(2i)(32)−(2i)2
Since i2=−1, this last fraction can be reduced simplified to
24+16i−3i+29−(−4)=26+13i13
which simplifies further to 2+i. Therefore, when 8−i3−2i is rewritten in the standard form a + bi, the value of a is 2.
In triangle ABC, the measure of ∠B is 90°, BC=16, and AC=20. Triangle DEF is similar to triangle ABC, where vertices D, E, and F correspond to vertices A, B, and C, respectively, and each side of triangle DEF is 13 the length of the corresponding side of triangle ABC. What is the value of sinF?
ANSWER EXPLANATION: Triangle ABC is a right triangle with its right angle at B. Therefore, AC is the hypotenuse of right triangle ABC, and AB and BC are the legs of right triangle ABC. According to the Pythagorean theorem,
AB=202−162=400−256=144=12
Since triangle DEF is similar to triangle ABC, with vertex F corresponding to vertex C, the measure of angle∠F equals the measure of angle∠C. Therefore, sinF=sinC. From the side lengths of triangle ABC,
sinF=oppositesidehypotenuse=ABAC=1220=35
Therefore, sinF=35.
The final answer is 35 or 0.6.
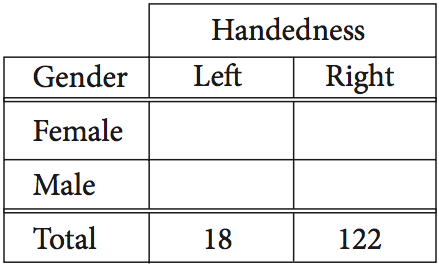
The incomplete table above summarizes the number of left-handed students and right-handed students by gender for the eighth grade students at Keisel Middle School. There are 5 times as many right-handed female students as there are left-handed female students, and there are 9 times as many right-handed male students as there are left-handed male students. if there is a total of 18 left-handed students and 122 right-handed students in the school, which of the following is closest to the probability that a right-handed student selected at random is female? (Note: Assume that none of the eighth-grade students are both right-handed and left-handed.)
A) 0.410 B) 0.357 C) 0.333 D) 0.250
ANSWER EXPLANATION: In order to solve this problem, you should create two equations using two variables (x and y) and the information you're given. Let x be the number of left-handed female students and let y be the number of left-handed male students. Using the information given in the problem, the number of right-handed female students will be 5x and the number of right-handed male students will be 9y. Since the total number of left-handed students is 18 and the total number of right-handed students is 122, the system of equations below must be true:
When you solve this system of equations, you get x=10 and y=8. Thus, 5*10, or 50, of the 122 right-handed students are female. Therefore, the probability that a right-handed student selected at random is female is 50122, which to the nearest thousandth is 0.410.
Questions 8 & 9
Use the following information for both question 7 and question 8.
If shoppers enter a store at an average rate of r shoppers per minute and each stays in the store for average time of T minutes, the average number of shoppers in the store, N, at any one time is given by the formula N=rT. This relationship is known as Little's law.
The owner of the Good Deals Store estimates that during business hours, an average of 3 shoppers per minute enter the store and that each of them stays an average of 15 minutes. The store owner uses Little's law to estimate that there are 45 shoppers in the store at any time.
Little's law can be applied to any part of the store, such as a particular department or the checkout lines. The store owner determines that, during business hours, approximately 84 shoppers per hour make a purchase and each of these shoppers spend an average of 5 minutes in the checkout line. At any time during business hours, about how many shoppers, on average, are waiting in the checkout line to make a purchase at the Good Deals Store?
ANSWER EXPLANATION: Since the question states that Little's law can be applied to any single part of the store (for example, just the checkout line), then the average number of shoppers, N, in the checkout line at any time is N=rT, where r is the number of shoppers entering the checkout line per minute and T is the average number of minutes each shopper spends in the checkout line.
Since 84 shoppers per hour make a purchase, 84 shoppers per hour enter the checkout line. However, this needs to be converted to the number of shoppers per minute (in order to be used with T=5). Since there are 60 minutes in one hour, the rate is 84shoppersperhour60minutes=1.4 shoppers per minute. Using the given formula with r=1.4 and T=5 yields
N=rt=(1.4)(5)=7
Therefore, the average number of shoppers, N, in the checkout line at any time during business hours is 7.
The final answer is 7.
The owner of the Good Deals Store opens a new store across town. For the new store, the owner estimates that, during business hours, an average of 90 shoppers per hour enter the store and each of them stays an average of 12 minutes. The average number of shoppers in the new store at any time is what percent less than the average number of shoppers in the original store at any time? (Note: Ignore the percent symbol when entering your answer. For example, if the answer is 42.1%, enter 42.1)
ANSWER EXPLANATION: According to the original information given, the estimated average number of shoppers in the original store at any time (N) is 45. In the question, it states that, in the new store, the manager estimates that an average of 90 shoppers per hour (60 minutes) enter the store, which is equivalent to 1.5 shoppers per minute (r). The manager also estimates that each shopper stays in the store for an average of 12 minutes (T). Thus, by Little's law, there are, on average, N=rT=(1.5)(12)=18 shoppers in the new store at any time. This is
45−1845*100=60
percent less than the average number of shoppers in the original store at any time.
The final answer is 60.
Question 10
In the xy-plane, the point (p,r) lies on the line with equation y=x+b, where b is a constant. The point with coordinates (2p,5r) lies on the line with equation y=2x+b. If p≠0, what is the value of rp?
ANSWER EXPLANATION: Since the point (p,r) lies on the line with equation y=x+b, the point must satisfy the equation. Substituting p for x and r for y in the equation y=x+b gives r=p+b, or b = r−p.
Similarly, since the point (2p,5r) lies on the line with the equation y=2x+b, the point must satisfy the equation. Substituting 2p for x and 5r for y in the equation y=2x+b gives:
Next, we can set the two equations equal to b equal to each other and simplify:
b=r−p=5r−4p
Finally, to find rp, we need to divide both sides of the equation by p and by 4:
The correct answer is B , 34.
If you picked choices A and D, you may have incorrectly formed your answer out of the coefficients in the point (2p,5r). If you picked Choice C, you may have confused r and p.
Note that while this is in the calculator section of the SAT, you absolutely do not need your calculator to solve it!
Question 11
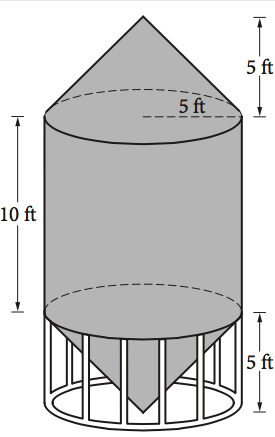
A) 261.8 B) 785.4 C) 916.3 D) 1047.2
ANSWER EXPLANATION: The volume of the grain silo can be found by adding the volumes of all the solids of which it is composed (a cylinder and two cones). The silo is made up of a cylinder (with height 10 feet and base radius 5 feet) and two cones (each with height 5 ft and base radius 5 ft). The formulas given at the beginning of the SAT Math section:
Volume of a Cone
Volume of a Cylinder
can be used to determine the total volume of the silo. Since the two cones have identical dimensions, the total volume, in cubic feet, of the silo is given by
Vsilo=π(52)(10)+(2)(13)π(52)(5)=(43)(250)π
which is approximately equal to 1,047.2 cubic feet.
Question 12
If x is the average (arithmetic mean) of m and 9, y is the average of 2m and 15, and z is the average of 3m and 18, what is the average of x, y, and z in terms of m?
A) m+6 B) m+7 C) 2m+14 D) 3m+21
ANSWER EXPLANATION: Since the average (arithmetic mean) of two numbers is equal to the sum of the two numbers divided by 2, the equations x=m+92, y=2m+152, z=3m+182are true. The average of x, y, and z is given by x+y+z3. Substituting the expressions in m for each variable (x, y, z) gives
[m+92+2m+152+3m+182]3
This fraction can be simplified to m+7.
Question 13
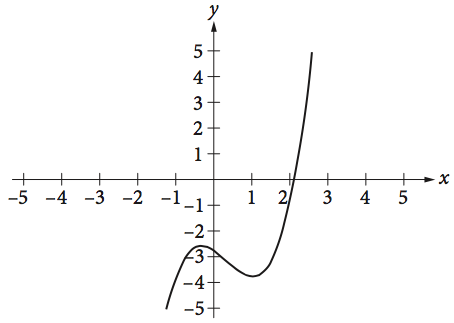
The function f(x)=x3−x2−x−114 is graphed in the xy-plane above. If k is a constant such that the equation f(x)=k has three real solutions, which of the following could be the value of k?
ANSWER EXPLANATION: The equation f(x)=k gives the solutions to the system of equations
y=f(x)=x3−x2−x−114
A real solution of a system of two equations corresponds to a point of intersection of the graphs of the two equations in the xy-plane.
The graph of y=k is a horizontal line that contains the point (0,k) and intersects the graph of the cubic equation three times (since it has three real solutions). Given the graph, the only horizontal line that would intersect the cubic equation three times is the line with the equation y=−3, or f(x)=−3. Therefore, k is −3.
Question 14
The dynamic pressure q generated by a fluid moving with velocity v can be found using the formula above, where n is the constant density of the fluid. An aeronautical engineer users the formula to find the dynamic pressure of a fluid moving with velocity v and the same fluid moving with velocity 1.5v. What is the ratio of the dynamic pressure of the faster fluid to the dynamic pressure of the slower fluid?
ANSWER EXPLANATION: To solve this problem, you need to set up to equations with variables. Let q1 be the dynamic pressure of the slower fluid moving with velocity v1, and let q2 be the dynamic pressure of the faster fluid moving with velocity v2. Then
Given the equation q=12nv2, substituting the dynamic pressure and velocity of the faster fluid gives q2=12n(v2)2. Since v2=1.5v1, the expression 1.5v1 can be substituted for v2 in this equation, giving q2=12n(1.5v1)2. By squaring 1.5, you can rewrite the previous equation as
q2=(2.25)(12)n(v1)2=(2.25)q1
Therefore, the ratio of the dynamic pressure of the faster fluid is
q2q1=2.25q1q1=2.25
The final answer is 2.25 or 9/4.
Question 15
For a polynomial p(x), the value of p(3) is −2. Which of the following must be true about p(x)?
A) x−5 is a factor of p(x). B) x−2 is a factor of p(x). C) x+2 is a factor of p(x). D) The remainder when p(x) is divided by x−3 is −2.
ANSWER EXPLANATION: If the polynomial p(x) is divided by a polynomial of the form x+k (which accounts for all of the possible answer choices in this question), the result can be written as
p(x)x+k=q(x)+rx+k
where q(x) is a polynomial and r is the remainder. Since x+k is a degree-1 polynomial (meaning it only includes x1 and no higher exponents), the remainder is a real number.
Therefore, p(x) can be rewritten as p(x)=(x+k)q(x)+r, where r is a real number.
The question states that p(3)=−2, so it must be true that
−2=p(3)=(3+k)q(3)+r
Now we can plug in all the possible answers. If the answer is A, B, or C, r will be 0, while if the answer is D, r will be −2.
A. −2=p(3)=(3+(−5))q(3)+0 −2=(3−5)q(3) −2=(−2)q(3)
This could be true, but only if q(3)=1
B. −2=p(3)=(3+(−2))q(3)+0 −2=(3−2)q(3) −2=(−1)q(3)
This could be true, but only if q(3)=2
C. −2=p(3)=(3+2)q(3)+0 −2=(5)q(3)
This could be true, but only if q(3)=−25
D. −2=p(3)=(3+(−3))q(3)+(−2) −2=(3−3)q(3)+(−2) −2=(0)q(3)+(−2)
This will always be true no matter what q(3) is.
Of the answer choices, the only one that must be true about p(x) is D, that the remainder when p(x) is divided by x−3 is -2.

You deserve all the naps after running through those questions.
What Do the Hardest SAT Math Questions Have in Common?
It's important to understand what makes these hard questions "hard." By doing so, you'll be able to both understand and solve similar questions when you see them on test day, as well as have a better strategy for identifying and correcting your previous SAT math errors.
In this section, we'll look at what these questions have in common and give examples of each type. Some of the reasons why the hardest math questions are the hardest math questions is because they:
#1: Test Several Mathematical Concepts at Once

Here, we must deal with imaginary numbers and fractions all at once.
Secret to success: Think of what applicable math you could use to solve the problem, do one step at a time, and try each technique until you find one that works!
#2: Involve a Lot of Steps
Remember: the more steps you need to take, the easier to mess up somewhere along the line!
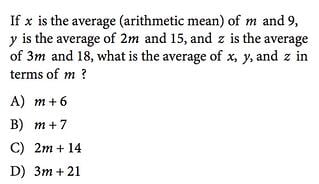
We must solve this problem in steps (doing several averages) to unlock the rest of the answers in a domino effect. This can get confusing, especially if you're stressed or running out of time.
Secret to success: Take it slow, take it step by step, and double-check your work so you don't make mistakes!
#3: Test Concepts That You Have Limited Familiarity With
For example, many students are less familiar with functions than they are with fractions and percentages, so most function questions are considered "high difficulty" problems.
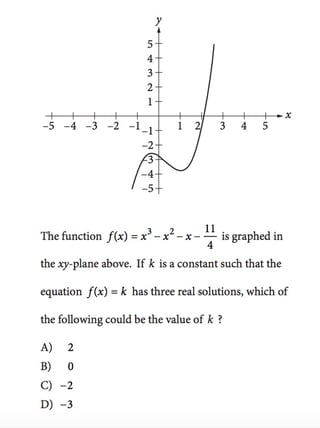
If you don't know your way around functions , this would be a tricky problem.
Secret to success: Review math concepts that you don't have as much familiarity with such as functions . We suggest using our great free SAT Math review guides .
#4: Are Worded in Unusual or Convoluted Ways
It can be difficult to figure out exactly what some questions are asking , much less figure out how to solve them. This is especially true when the question is located at the end of the section, and you are running out of time.

Because this question provides so much information without a diagram, it can be difficult to puzzle through in the limited time allowed.
Secret to success: Take your time, analyze what is being asked of you, and draw a diagram if it's helpful to you.
#5: Use Many Different Variables

With so many different variables in play, it is quite easy to get confused.
Secret to success: Take your time, analyze what is being asked of you, and consider if plugging in numbers is a good strategy to solve the problem (it wouldn't be for the question above, but would be for many other SAT variable questions).
The Take-Aways
The SAT is a marathon and the better prepared you are for it, the better you'll feel on test day. Knowing how to handle the hardest questions the test can throw at you will make taking the real SAT seem a lot less daunting.
If you felt that these questions were easy, make sure not underestimate the effect of adrenaline and fatigue on your ability to solve problems. As you continue to study, always adhere to the proper timing guidelines and try to take full tests whenever possible. This is the best way to recreate the actual testing environment so that you can prepare for the real deal.
If you felt these questions were challenging, be sure to strengthen your math knowledge by checking out our individual math topic guides for the SAT . There, you'll see more detailed explanations of the topics in question as well as more detailed answer breakdowns.
What's Next?
Felt that these questions were harder than you were expecting? Take a look at all the topics covered in the SAT math section and then note which sections were particular difficulty for you. Next, take a gander at our individual math guides to help you shore up any of those weak areas.
Running out of time on the SAT math section? Our guide will help you beat the clock and maximize your score .
Aiming for a perfect score? Check out our guide on how to get a perfect 800 on the SAT math section , written by a perfect-scorer.
Trending Now
How to Get Into Harvard and the Ivy League
How to Get a Perfect 4.0 GPA
How to Write an Amazing College Essay
What Exactly Are Colleges Looking For?
ACT vs. SAT: Which Test Should You Take?
When should you take the SAT or ACT?
Get Your Free

Find Your Target SAT Score
Free Complete Official SAT Practice Tests
How to Get a Perfect SAT Score, by an Expert Full Scorer
Score 800 on SAT Math
Score 800 on SAT Reading and Writing
How to Improve Your Low SAT Score
Score 600 on SAT Math
Score 600 on SAT Reading and Writing
Find Your Target ACT Score
Complete Official Free ACT Practice Tests
How to Get a Perfect ACT Score, by a 36 Full Scorer
Get a 36 on ACT English
Get a 36 on ACT Math
Get a 36 on ACT Reading
Get a 36 on ACT Science
How to Improve Your Low ACT Score
Get a 24 on ACT English
Get a 24 on ACT Math
Get a 24 on ACT Reading
Get a 24 on ACT Science
Stay Informed
Get the latest articles and test prep tips!

Courtney scored in the 99th percentile on the SAT in high school and went on to graduate from Stanford University with a degree in Cultural and Social Anthropology. She is passionate about bringing education and the tools to succeed to students from all backgrounds and walks of life, as she believes open education is one of the great societal equalizers. She has years of tutoring experience and writes creative works in her free time.
Ask a Question Below
Have any questions about this article or other topics? Ask below and we'll reply!
Open Middle®


- Mathematicians
- Math Lessons
- Square Roots
- Math Calculators
Hard Algebra Questions – Challenging Problems and Step-by-Step Solutions
JUMP TO TOPIC
Understanding the Fundamentals of Algebra
Solving algebraic operations, linear equations and their graphs, solving quadratic equations, systems of equations, applications of algebra.

Algebra is a fundamental branch of mathematics that deals with symbols and the rules for manipulating these symbols . In its most basic form, it is about finding the unknowns or the variables within equations.
As a student progresses, the questions in algebra can evolve from simple linear equations to more complex problems involving multiple steps, functions, or advanced concepts. Advanced algebra questions often probe one’s understanding of concepts like polynomial functions, rational expressions, exponents, and logarithms.
Navigating the web for reliable and challenging algebra problems and solutions I’ve found to be quite a task, but essential for anyone looking to master the subject. Websites and apps aimed at providing mathematics resources offer a range of problems, from basic to complex, helping learners tackle various topics effectively.
Engaging with these platforms allows for practice and reinforcement of algebraic concepts, which is crucial for solidifying one’s understanding and proficiency in mathematics.
I have to admit, that algebra can sometimes seem like a puzzle with a missing piece. But it’s that moment of clarity when the pieces fall into place that makes solving algebra questions incredibly rewarding. Stick around as we explore some hard algebra questions along with their solutions – the satisfaction of cracking them is just around the corner.
Algebra can seem challenging, but by grasping some key concepts, I can work through even the tough problems.

The backbone of algebra is the equation, which is a statement that two expressions are equal, often containing an unknown quantity, usually represented by a letter like ( x ) or ( y ).
For instance, in the equation ( x + 3 = 7 ), my goal is to find the value of ( x ) that makes this statement true. To do this, I simplify the equation to find ( x ). Simplification might involve combining like terms or using inverse operations. So, in this case, I subtract 3 from both sides to isolate ( x ), yielding ( x = 4 ).
Inequalities are like equations, but instead of equality, they express a relation where one value is larger or smaller than another. This can be represented by symbols such as “>,” “<,” “≤,” or “≥.” For example, if I have ( x – 5 > 10 ), I’m looking for all values of ( x ) that make this inequality true.
Solving this, I add 5 to both sides to get ( x > 15 ).
Here’s a simple way to visualize the process of solving an inequality :
| Steps | Example |
|---|---|
| Write down the inequality | ( x – 5 > 10 ) |
| Perform the same operation on both sides | ( x – 5 + 5 > 10 + 5 ) |
| Simplify to find the solution | ( x > 15 ) |
Remember, if I multiply or divide both sides of an inequality by a negative number, the direction of the inequality sign flips. So, if I had ( -2x < 8 ), by dividing both sides by -2, it becomes ( x > -4 ).
Understanding the foundation allows me to simplify and solve equations and inequalities, providing the confidence to tackle more complex algebraic questions.
When I approach algebraic operations, I prioritize understanding the core concepts—exponents, factoring, complex numbers, and simplification.

These elements are the building blocks to solving more intricate algebra problems.
For exponents , remember that the base raised to the power of an exponent reflects how many times the base is multiplied by itself. For instance, $3^4$ means $3 \times 3 \times 3 \times 3$. When dealing with exponents, it’s essential to be familiar with the laws of exponents for simplification purposes.
| Law | Equation |
|---|---|
| Product of Powers | $a^m \cdot a^n = a^{m+n}$ |
| Quotient of Powers | $\frac{a^m}{a^n} = a^{m-n}$ |
| Power of a Power | $(a^m)^n = a^{m \cdot n}$ |
| Power of a Product | $(ab)^n = a^n \cdot b^n$ |
Next is factoring . I look for the greatest common factor (GCF) or use techniques like the difference of squares, and the quadratic formula for trinomials. For example, factoring $x^2 – 9$ would yield $(x + 3)(x – 3)$ because it is the difference of squares.
When it comes to complex numbers , which are in the form $a + bi$, where $i$ is the imaginary unit $(i^2 = -1)$, I remember that these numbers can be added, subtracted, and multiplied just like real numbers, with special attention to the property of $i$.
Finally, simplification is a matter of combining like terms and using the distributive property where necessary. For instance, to simplify the expression $2(x + 3) + x$, I first distribute the $2$ to get $2x + 6 + x$ and combine like terms to get $3x + 6$.
By mastering these components, I set a strong foundation for tackling hard algebra questions effectively.
Solving Advanced Algebraic Equations
Advanced algebra often serves as the foundation for calculus, statistics, and even programming. Let’s take a look at some of the core types of equations and how to approach them, including linear, quadratic, and systems of equations.
I’ll start by discussing linear equations , characterized by their straight-line graphs. A basic form of a linear equation is the slope-intercept form, expressed as ( y = mx + b ), where ( m ) is the slope and ( b ) is the y-intercept. Converting to standard form , ( Ax + By = C ), may be necessary for some applications. To graph these equations, I find two points by plugging in values for ( x ) and then plotting those points. Connecting these will give me a straight line.
Moving on to quadratic equations , these are typically presented in the general form ( a$x^2$ + bx + c = 0 ). These equations form parabolas when graphed.
I can solve quadratic equations using methods such as factoring, completing the square, or using the quadratic formula, ( x = $\frac{-b \pm \sqrt{b^2 – 4ac}}{2a}$ ). Each method has its own use cases; for example, factoring is efficient when the equation easily decomposes into binomials.
Lastly, I’ll tackle systems of equations , where I have to find the solution set of two or more equations. When solving linear systems , I can use methods such as substitution, elimination, or graphing.
Substitution involves solving one equation for a variable and then substituting that expression into the other equation, while elimination adds or subtracts equations to eliminate a variable. Graphing requires drawing lines of each equation to find their point of intersection.
| Method | When to Use It |
|---|---|
| Substitution | One variable is easily isolated |
| Elimination | Equations can be easily summed or subtracted to cancel out a variable |
| Graphing | Ideal for visual learners and small systems |
These are standard approaches that I often use to find the solutions to various types of algebraic equations.
Algebra has countless applications in the real world, and one of the most practical applications is in calculating areas and perimeters of geometric shapes. Let me guide you through some examples:
Area of a Rectangle : To find the area of a rectangle, I use the formula:
$$ A = l \times w $$
where ( A ) represents the area, ( l ) is the length, and ( w ) is the width.
Perimeter of a Rectangle : Similarly, finding the perimeter is just as straightforward with the equation:
$$ P = 2(l + w) $$
where ( P ) stands for the perimeter.
Area of a Circle : When I look at circles, the area is found using:
$$ A = \pi r^2 $$
Here, ( A ) is the area and ( r ) is the radius of the circle.
Circumference of a Circle: And for the circumference, which is the perimeter of a circle, the formula is:
$$ C = 2\pi r $$
where ( C ) is the circumference.
| Shape | Formula for Area | Formula for Perimeter/Circumference |
|---|---|---|
| Rectangle | ( A = l \times w ) | ( P = 2(l + w) ) |
| Circle | ( A = $\pi r^2$ ) | ( C = 2$\pi$ r ) |
Understanding these formulas allows me to solve real-life problems, such as calculating the amount of paint needed to cover a wall or the fencing required for a circular garden.
With the help of algebra, I can create equations from word problems and solve them; the results help me make informed decisions and solve practical problems efficiently.
In our exploration of challenging algebra questions , I’ve presented a range of problems that test our understanding and application of algebraic concepts. From the intricacies of trigonometric equations to the puzzles of algebraic word problems, the journey through these issues illuminates the beauty of mathematics.
I sincerely hope that the solutions and strategies discussed have helped shed light on the complexity and elegance of algebra. Remember, practicing these tough problems not only sharpens your skills but also prepares you for more advanced mathematical challenges.
Whether you’re preparing for exams or simply indulging in the joy of problem-solving, the resilience and adaptability gained here are invaluable.
Algebra does not always yield its secrets easily, but patience and persistence in working through these tough problems can be immensely rewarding. Keep this momentum going, continue nurturing your mathematical curiosity, and let your confidence grow with each equation you solve.
- Pre Calculus
- Probability
- Sets & Set Theory
- Trigonometry
- Member login
- Pre-algebra lessons
- Pre-algebra word problems
- Algebra lessons
- Algebra word problems
- Algebra proofs
- Advanced algebra
- Geometry lessons
- Geometry word problems
- Geometry proofs
- Trigonometry lessons
- Consumer math
- Baseball math
- Math for nurses
- Statistics made easy
- High school physics
- Basic mathematics store
- SAT Math Prep
- Math skills by grade level
- Ask an expert
- Other websites
- K-12 worksheets
- Worksheets generator
- Algebra worksheets
- Geometry worksheets
- Free math problem solver
- Pre-algebra calculators
- Algebra Calculators
- Geometry Calculators
- Math puzzles
- Math tricks
100 hard word problems in algebra
Find below a wide variety of hard word problems in algebra. Most tricky and tough algebra word problems are covered here. If you can solve these, you can probably solve any algebra problems. Teachers! Feel free to select from this list and give them to your students to see if they have mastered how to solve tough algebra problems. Find out below how you can print these problems. You can also purchase a solution if needed.

1. The cost of petrol rises by 2 cents a liter. last week a man bought 20 liters at the old price. This week he bought 10 liters at the new price. Altogether, the petrol costs $9.20. What was the old price for 1 liter?
2. Teachers divided students into groups of 3. Each group of 3 wrote a report that had 9 pictures in it. The students used 585 pictures altogether. How many students were there in all?
3. Vera and Vikki are sisters. Vera is 4 years old and Vikki is 13 years old. What age will each sister be when Vikki is twice as old as Vera?
4. A can do a work in 14 days and working together A and B can do the same work in 10 days. In what time can B alone do the work?
5. 7 workers can make 210 pairs of cup in 6 days. How many workers are required to make 450 pairs of cup in 10 days?
6. Ten years ago the ratio between the ages of Mohan and Suman was 3:5. 11 years hence it will be 11:16. What is the present age of Mohan?
7. The ratio of girls to boys in class is 9 to 7 and there are 80 students in the class. How many girls are in the class?
8. One ounce of solution X contains only ingredients a and b in a ratio of 2:3. One ounce of solution Y contains only ingredients a and b in a ratio of 1:2. If solution Z is created by mixing solutions X and Y in a ratio of 3:11, then 2520 ounces of solution Z contains how many ounces of a?
9. This week Bob puts gas in his truck when the tank was about half empty. Five days later, bob puts gas again when the tank was about three fourths full. If Bob Bought 24 gallons of gas, how many gallons does the tank hold?
10. A commercial airplane flying with a speed of 700 mi/h is detected 1000 miles away with a radar. Half an hour later an interceptor plane flying with a speed of 800 mi/h is dispatched. How long will it take the interceptor plane to meet with the other plane?
11. There are 40 pigs and chickens in a farmyard. Joseph counted 100 legs in all. How many pigs and how many chickens are there?
12. The top of a box is a rectangle with a perimeter of 72 inches. If the box is 8 inches high, what dimensions will give the maximum volume?
13. You are raising money for a charity. Someone made a fixed donation of 500. Then, you require each participant to make a pledge of 25 dollars. What is the minimum amount of money raised if there are 224 participants.
14. The sum of two positive numbers is 4 and the sum of their squares is 28. What are the two numbers?
15. Flying against the jet stream, a jet travels 1880 mi in 4 hours. Flying with the jet stream, the same jet travels 5820 mi in 6 hours. What is the rate of the jet in still air and what is the rate of the jet stream?
16. Jenna and her friend, Khalil, are having a contest to see who can save the most money. Jenna has already saved $110 and every week she saves an additional $20. Khalil has already saved $80 and every week he saves an additional $25. Let x represent the number of weeks and y represent the total amount of money saved. Determine in how many weeks Jenna and Khalil will have the same amount of money.
17. The sum of three consecutive terms of a geometric sequence is 104 and their product is 13824.find the terms.
18. The sum of the first and last of four consecutive odd integers is 52. What are the four integers?
19. A health club charges a one-time initiation fee and a monthly fee. John paid 100 dollars for 2 months of membership. However, Peter paid 200 for 6 months of membership. How much will Sylvia pay for 1 year of membership?
20. The sum of two positive numbers is 4 and the sum of their cubes is 28. What is the product of the two numbers?
21. A man selling computer parts realizes that when he sells 16 computer parts, his earning is $1700. When he sells 56 computer parts, his earning is $4300. What will the earning be if the man sells 30 computers parts?
22. A man has 15 coins in his pockets. These coins are dimes and quarters that add up 2.4 dollars. How many quarters and how many dimes does the man have?
23. The lengths of the sides of a triangle are in the ratio 4:3:5. Find the lengths of the sides if the perimeter is 18 inches.
24. The ratio of base to height of a equilateral triangle is 3:4. If the area of the triangle is 6, what is the perimeter of the triangle?
25. The percent return rate of a growth fund, income fund, and money market are 10%, 7%, and 5% respectively. Suppose you have 3200 to invest and you want to put twice as much in the growth fund as in the money market to maximize your return. How should you invest to get a return of 250 dollars in 1 year?
26. A shark was caught whose tail weighted 200 pounds. The head of the shark weighted as much as its tail plus half its body. Its body weighted as much as its head and tail. What is the weight of the shark?
27. The square root of a number plus two is the same as the number. What is the number?
28. Suppose you have a coupon worth 6 dollars off any item at a mall. You go to a store at the mall that offers a 20% discount. What do you need to do to save the most money?
29. Suppose your grades on three math exams are 80, 93, and 91. What grade do you need on your next exam to have at least a 90 average on the four exams?
30. Peter has a photograph that is 5 inches wide and 6 inches long. She enlarged each side by the same amount. By how much was the photograph enlarged if the new area is 182 square inches?
31. The cost to produce a book is 1200 to get started plus 9 dollars per book. The book sells for 15 dollars each. How many books must be sold to make a profit?
32. Store A sells CDs for 2 dollars each if you pay a one-time fee of 104 dollars. Store B offers 12 free CDs and charges 10 dollars for each additional CD. How many CD must you buy so it will cost the same under both plans?
33. When 4 is added to two numbers, the ratio is 5:6. When 4 is subtracted from the two numbers, the ratio is 1:2. Find the two numbers.
34. A store owner wants to sell 200 pounds of pistachios and walnuts mixed together. Walnuts cost 4 dollars per pound and pistachio cost 6 dollars per pounds. How many pounds of each type of nuts should be mixed if the store owner will charge 5 dollars for the mixture?
35. A cereal box manufacturer makes 32-ounce boxes of cereal. In a perfect world, the box will be 32-ounce every time is made. However, since the world is not perfect, they allow a difference of 0.06 ounce. Find the range of acceptable size for the cereal box.
36. A man weighing 600 kg has been losing 3.12% of his weight each month with some heavy exercises and eating the right food. What will the man weigh after 20 months?
37. An object is thrown into the air at a height of 60 feet. After 1 second and 2 second, the object is 88 feet and 84 feet in the air respectively. What is the initial speed of the object?
38. A transit is 200 feet from the base of a building. There is man standing on top of the building. The angles of elevation from the top and bottom of the man are 45 degrees and 44 degrees. What is the height of the man?
39. A lemonade consists of 6% of lemon juice and a strawberry juice consists of 15% pure fruit juice. How much of each kind should be mixed together to get a 4 Liters of a 10% concentration of fruit juice?
40. Ellen can wash her car in 60 minutes. Her older sister Sarah can do the same job in 45 minutes. How long will it take if they wash the car together?
41. A plane flies 500 mi/h. The plane can travel 1100 miles with the wind in the same amount of time as it travels 900 miles against the wind. What is the speed of the wind?
42. A company produces boxes that are 5 feet long, 4 feet wide, and 3 feet high. The company wants to increase each dimension by the same amount so that the new volume is twice as big. How much is the increase in dimension?
43. James invested half of his money in land, a tenth in stock, and a twentieth in saving bonds. Then, he put the remaining 21000 in a CD. How much money did James saved or invested?
44. The motherboards for a desktop computer can be manufactured for 50 dollars each. The development cost is 250000. The first 20 motherboard are samples and will not be sold. How many salable motherboards will yield an average cost of 6325 dollars?
45. How much of a 70% orange juice drink must be mixed with 44 gallons of a 20% orange juice drink to obtain a mixture that is 50% orange juice?
46. A company sells nuts in bulk quantities. When bought in bulk, peanuts sell for $1.20 per pound, almonds for $ 2.20 per pound, and cashews for $3.20 per pound. Suppose a specialty shop wants a mixture of 280 pounds that will cost $2.59 per pound. Find the number of pounds of each type of nut if the sum of the number of pounds of almonds and cashews is three times the number of pounds of peanuts. Round your answers to the nearest pound.
47. A Basketball player has successfully made 36 of his last 48 free throws. Find the number of consecutive free throws the player needs to increase his success rate to 80%.
48. John can wash cars 3 times as fast as his son Erick. Working together, they need to wash 30 cars in 6 hours. How many hours will it takes each of them working alone?
49. In a college, about 36% of student are under 20 years old and 15% are over 40 years old. What is the probability that a student chosen at random is under 20 years old or over 40 years?
50. Twice a number plus the square root of the number is twelve minus the square root of the number.
51. The light intensity, I , of a light bulb varies inversely as the square of the distance from the bulb. A a distance of 3 meters from the bulb, I = 1.5 W/m^2 . What is the light intensity at a distance of 2 meters from the bulb?
52. The lengths of two sides of a triangle are 2 and 6. find the range of values for the possible lengths of the third side.
53. Find three consecutive integers such that one half of their sum is between 15 and 21.
54. After you open a book, you notice that the product of the two page numbers on the facing pages is 650. What are the two page numbers?
55. Suppose you start with a number. You multiply the number by 3, add 7, divide by ½, subtract 5, and then divide by 12. The result is 5. What number did you start with?
56. You have 156 feet of fencing to enclose a rectangular garden. You want the garden to be 5 times as long as it is wide. Find the dimensions of the garden.
57. The amount of water a dripping faucet wastes water varies directly with the amount of time the faucet drips. If the faucet drips 2 cups of water every 6 minutes, find out how long it will take the faucet to drip 10.6465 liters of water.
58. A washer costs 25% more than a dryer. If the store clerk gave a 10% discount for the dryer and a 20% discount for the washer, how much is the washer before the discount if you paid 1900 dollars.
59. Baking a tray of blueberry muffins takes 4 cups of milk and 3 cups of wheat flour. A tray of pumpkin muffins takes 2 cups of milk and 3 cups of wheat flour. A baker has 16 cups of milk and 15 cups of wheat flour. You make 3 dollars profit per tray of blueberry muffins and 2 dollars profit per tray of pumpkin muffins. How many trays of each type of muffins should you make to maximize profit?
60. A company found that -2p + 1000 models the number of TVs sold per month where p can be set as low as 200 or as high as 300. How can the company maximize the revenue?
More hard word problems in algebra
61. Your friends say that he has $2.40 in equal numbers of quarters, dimes, and nickels. How many of each coin does he have?
62. I am a two-digit number whose digit in the tenth place is 1 less than twice the digit in the ones place. When the digit in the tenth place is divided by the digit in the ones place, The quotient is 1 and the remainder is 4. What number am I?
63. A two-digit number is formed by randomly selecting from the digits 2, 4, 5, and 7 without replacement. What is the probability that a two-digit number contains a 2 or a 7?
64. Suppose you interview 30 females and 20 males at your school to find out who among them are using an electric toothbrush. Your survey revealed that only 2 males use an electric toothbrush while 6 females use it. What is the probability that a respondent did not use an electric toothbrush given that the respondent is a female?
65. An employer pays 15 dollars per hour plus an extra 5 dollars per hour for every hour worked beyond 8 hours up to a maximum daily wage of 220 dollars. Find a piecewise function that models this situation.
66. Divide me by 7, the remainder is 5. Divide me by 3, the remainder is 1 and my quotient is 2 less than 3 times my previous quotient. What number am I?
67. A company making luggage have these requirements to follow. The length is 15 inches greater than the depth and the sum of length, width, and depth may not exceed 50 inches. What is the maximum value for the depth if the manufacturer will only use whole numbers?
68. To make an open box, a man cuts equal squares from each corner of a sheet of metal that is 12 inches wide and 16 inches long. Find an expression for the volume in terms of x.
69. Ten candidates are running for president, vice-president, and secretary in the students government. You may vote for as many as 3 candidates. In how many ways can you vote for 3 or fewer candidates?
70. The half-life of a medication prescribed by a doctor is 6 hours. How many mg of this medication is left after 78 hours if the doctor prescribed 100 mg?
71. Suppose you roll a red number cube and a yellow number cube. Find P(red 2, yellow 2) and the probability to get any matching pairs of numbers.
72. A movie theater in a small town usually open its doors 3 days in a row and then closes the next day for maintenance. Another movie theater 3 miles away open 4 days in a row and then closes the next day for the same reason. Suppose both movie theaters are closed today and today is Wednesday, when is the next time they will both be closed again on the same day?
73. An investor invests 5000 dollars at 10% and the rest at 5%. How much was invested at 5% if the yield is one-fifth of the amount invested at at 10%?
74. 20000 students took a standardized math test. The scores on the test are normally distributed, with a mean score of 85 and a standard deviation of 5. About how many students scored between 90 and 95?
75. A satellite, located 2400 km above Earth’s surface, is in circular orbit around the earth. If it takes the satellite 3 hours to complete 1 orbit, how far is the satellite after 1 hour?
76. In a group of 10 people, what is the probability that at least two people in the group have the same birthday?
77. During a fundraising for cancer at a gala, everybody shakes hands with everyone else in the room before the event and after the event is finished. If n people attended the gala, how many different handshakes occur?
78. Two cubes have side lengths that are equal to 2x and 4x. How many times greater than the surface of the small cube is the surface area of the large cube?
79. Suppose you have a job in a restaurant that pays $8 per hour. You also have a job at Walmart that pays $10 per hour. You want to earn at least 200 per week. However, you want to work no more than 25 hours per week . Show 3 different ways you could work at each job.
80. Two company offer tutoring services. Company A realizes that when they tutor for 3 hours, they make 45 dollars. When they tutor for 7 hours they make 105 hours. Company B realizes that when they tutor for 2 hours, they make 34 dollars. When they tutor for 6 hours they make 102 hours. Assuming that the number of hours students sign for tutoring is the same for both company, which company will generate more revenue?
81. You want to fence a rectangular area for kids in the backyard. To save on fences, you will use the back of your house as one of the four sides. Find the possible dimensions if the house is 60 feet wide and you want to use at least 160 feet of fencing.
82. When a number in increased by 20%, the result is the same when it is decreased by 10% plus 12. What is the number?
83. The average of three numbers is 47. The biggest number is five more than twice the smallest. The range is 35. What are the three numbers?
84. The percent of increase of a number from its original amount to 36 is 80%. What is the original amount of the number?
85. When Peter drives to work, he averages 45 miles per hour because of traffic. On the way back home, he averages 60 miles per hour because traffic is not as bad. The total travel time is 2 hours. How far is Peter’s house from work?
86. An advertising company takes 20% from all revenue that it generates for its affiliates. If the affiliates were paid 15200 dollars this month, how much revenue did the advertising company generate this month?
87. A company’s revenue can be modeled with a quadratic equation. The company noticed that when they sell either 2 or or 12 items, the revenue is 0. How much is the revenue when they sell 20 items?
88. A ball bounced 4 times, reaching three-fourths of its previous height with each bounce. After the fourth bounce, the ball reached a height of 25 cm. How high was the ball when it was dropped?
89. A rental company charges 40 dollars per day plus $0.30 per mile. You rent a car and drop it off 4 days later. How many miles did you drive the car if you paid 325.5 dollars which included a 5% sales tax?
90. Two students leave school at the same time and travel in opposite directions along the same road. One walk at a rate of 3 mi/h. The other bikes at a rate of 8.5 mi/h. After how long will they be 23 miles part?
91. Brown has the same number of brothers as sisters. His sister Sylvia as twice as many brothers as sisters. How many children are in the family?
92. Ethan has the same number of male classmates as female classmates. His classmate Olivia has three-fourths as many female classmates as male classmates. How many students are in the class?
93. Noah wants to share a certain amount of money with 10 people. However, at the last minute, he is thinking about decreasing the amount by 20 so he can keep 20 for himself and share the money with only 5 people. How much money is Noah trying to share if each person still gets the same amount?
94. The square root of me plus the square root of me is me. Who am I?
95. A cash drawer contains 160 bills, all 10s and 50s. If the total value of the 10s and 50s is $1,760. How many of each type of bill are in the drawer?
96. You want to make 28 grams of protein snack mix made with peanuts and granola. Peanuts contain 7 grams of protein per ounce and granola contain 3 grams of protein per ounce. How many ounces of granola should you use for 1 ounce of peanuts?
97. The length of a rectangular prism is quadrupled, the width is doubled, and the height is cut in half. If V is the volume of the rectangular prism before the modification, express the volume after the modification in terms of V.
98. A car rental has CD players in 85% of its cars. The CD players are randomly distributed throughout the fleet of cars. If a person rents 4 cars, what is the probability that at least 3 of them will have CD players?
99. Jacob’s hourly wage is 4 times as much as Noah. When Jacob got a raise of 2 dollars, Noah accepted a new position that pays him 2 dollars less per hour. Jacob now earns 5 times as much money as Noah. How much money do they make per hour after Jacob got the raise?
You own a catering business that makes specialty cakes. Your company has decided to create three types of cakes. To create these cakes, it takes a team that consists of a decorator, a baker, and a design consultant. Cake A takes the decorator 9 hours, the baker 6 hours, and the design consultant 1 hour to complete. Cake B takes the decorator 10 hours, the baker 4 hours, and the design consultant 2 hours. Cake C takes the decorator 12 hours, the baker 4 hour, and the design consultant 1 hour. Without hiring additional employees, there are 398 decorator hours available, 164 baker hours available, and 58 design consultant hours available. How many of each type of cake can be created?
Want a solution to these tough algebra problems? Add to your shopping cart and purchase a Detailed 150+ PAGES SOLUTION and TOP-NOTCH EXPLANATIONS with PayPal.
Hard word problems in algebra
Click here to print these problems
Applied math
Calculators.
100 Tough Algebra Word Problems. If you can solve these problems with no help, you must be a genius!

Recommended
About me :: Privacy policy :: Disclaimer :: Donate Careers in mathematics
Copyright © 2008-2021. Basic-mathematics.com. All right reserved
📬 Sign Up for Our Amazing Newsletter!
Writing result-oriented ad copy is difficult, as it must appeal to, entice, and convince consumers to take action.
How to Work Through Hard Math Problems
parent of one of our students wrote today about his daughter’s occasional frustration with the difficulty of some of the problems in our courses. She does fantastic work in our courses , and was easily among the very top students in the class she took with me, and yet she still occasionally hits problems that she can’t solve.
Moreover, she has access to an excellent math teacher in her school who sometimes can’t help her get past these problems, either. (This is no slight to him—I have students bring me problems I can’t solve, too!) Her question: “Why does it have to be so hard?”

The Case for Doing Hard Things
We ask hard questions because so many of the problems worth solving in life are hard. If they were easy, someone else would have solved them before you got to them. This is why college classes at top-tier universities have tests on which nearly no one clears 70%, much less gets a perfect score. They’re training future researchers, and the whole point of research is to find and answer questions that have never been solved. You can’t learn how to do that without fighting with problems you can’t solve. If you are consistently getting every problem in a class correct, you shouldn’t be too happy — it means you aren’t learning efficiently enough. You need to find a harder class.
The problem with not being challenged sufficiently goes well beyond not learning math (or whatever) as quickly as you can. I think a lot of what we do at AoPS is preparing students for challenges well outside mathematics. The same sort of strategies that go into solving very difficult math problems can be used to tackle a great many problems. I believe we’re teaching students how to think, how to approach difficult problems, and that math happens to be the best way to do so for many people.
The first step in dealing with difficult problems is to accept and understand their importance. Don’t duck them. They will teach you a lot more than a worksheet full of easy problems. Brilliant “Aha!” moments almost always spring from minds cultivated by long periods of frustration. But without that frustration, those brilliant ideas never arise.
Strategies for Difficult Math Problems — and Beyond
Here are a few strategies for dealing with hard problems, and the frustration that comes with them:
Do something . Yeah, the problem is hard. Yeah, you have no idea what to do to solve it. At some point you have to stop staring and start trying stuff. Most of it won’t work. Accept that a lot of your effort will appear to have been wasted. But there’s a chance that one of your stabs will hit something, and even if it doesn’t, the effort may prepare your mind for the winning idea when the time comes.
We started developing an elementary school curriculum months and months before we had the idea that became Beast Academy . Our lead curriculum developer wrote 100–200 pages of content, dreaming up lots of different styles and approaches we might use. Not a one of those pages will be in the final work, but they spurred a great many ideas for content we will use. Perhaps more importantly, it prepared us so that when we finally hit upon the Beast Academy idea, we were confident enough to pursue it.
Simplify the problem . Try smaller numbers and special cases. Remove restrictions. Or add restrictions. Set your sights a little lower, then raise them once you tackle the simpler problem.
Reflect on successes . You’ve solved lots of problems. Some of them were even hard problems! How did you do it? Start with problems that are similar to the one you face, but also think about others that have nothing to do with your current problem. Think about the strategies you used to solve those problems, and you might just stumble on the solution.
A few months ago, I was playing around with some Project Euler problems, and I came upon a problem that (eventually) boiled down to generating integer solutions to c ² = a ² + b ² + ab in an efficient manner. Number theory is not my strength, but my path to the solution was to recall first the method for generating Pythagorean triples. Then, I thought about how to generate that method, and the path to the solution became clear. (I’m guessing some of our more mathematically advanced readers have so internalized the solution process for this type of Diophantine equation that you don’t have to travel with Pythagoras to get there!)
Focus on what you haven’t used yet . Many problems (particularly geometry problems) have a lot of moving parts. Look back at the problem, and the discoveries you have made so far and ask yourself: “What haven’t I used yet in any constructive way?” The answer to that question is often the key to your next step.
Work backwards . This is particularly useful when trying to discover proofs. Instead of starting from what you know and working towards what you want, start from what you want, and ask yourself what you need to get there.
Ask for help . This is hard for many outstanding students. You’re so used to getting everything right, to being the one everyone else asks, that it’s hard to admit you need help. When I first got to the Mathematical Olympiad Program (MOP) my sophomore year, I was in way over my head. I understood very little of anything that happened in class. I asked for help from the professor once — it was very hard to get up the courage to do so. I didn’t understand anything he told me during the 15 minutes he worked privately with me. I just couldn’t admit it and ask for more help, so I stopped asking. I could have learned much, much more had I just been more willing to admit to people that I just didn’t understand. (This is part of why our classes now have a feature that allows students to ask questions anonymously.) Get over it. You will get stuck. You will need help. And if you ask for it, you’ll get much farther than if you don’t.
Start early . This doesn’t help much with timed tests, but with the longer-range assignments that are parts of college and of life, it’s essential. Don’t wait until the last minute — hard problems are hard enough without having to deal with time pressure. Moreover, complex ideas take a long time to understand fully. The people you know who seem wicked smart, and who seem to come up with ideas much faster than you possibly could, are often people who have simply thought about the issues for much longer than you have. I used this strategy throughout college to great success — in the first few weeks of each semester, I worked far ahead in all of my classes. Therefore, by the end of the semester, I had been thinking about the key ideas for a lot longer than most of my classmates, making the exams and such at the end of the course a lot easier.
Take a break . Get away from the problem for a bit. When you come back to it, you may find that you haven’t entirely gotten away from the problem at all — the background processes of your brain have continued plugging away, and you’ll find yourself a lot closer to the solution. Of course, it’s a lot easier to take a break if you start early.
Start over . Put all your earlier work aside, get a fresh sheet of paper, and try to start from scratch. Your other work will still be there if you want to draw from it later, and it may have prepared you to take advantage of insights you make in your second go-round.
Give up . You won’t solve them all. At some point, it’s time to cut your losses and move on. This is especially true when you’re in training, and trying to learn new things. A single difficult problem is usually going to teach you more in the first hour or two than it will in the next six, and there are a lot more problems to learn from. So, set yourself a time limit, and if you’re still hopelessly stuck at the end of it, then read the solutions and move on.
Be introspective . If you do give up and read the solution, then read it actively, not passively. As you read it, think about what clues in the problem could have led you to this solution. Think about what you did wrong in your investigation. If there are math facts in the solution that you don’t understand, then go investigate. I was completely befuddled the first time I saw a bunch of stuff about “mod”s in an olympiad solution — we didn’t have the internet then, so I couldn’t easily find out how straightforward modular arithmetic is! You have the internet now, so you have no excuse. If you did solve the problem, don’t just pat yourself on the back. Think about the key steps you made, and what the signs were to try them. Think about the blind alleys you explored en route to the solution, and how you could have avoided them. Those lessons will serve you well later.
Come back . If you gave up and looked at the solutions, then come back and try the problem again a few weeks later. If you don’t have any solutions to look at, keep the problem alive. Store it away on paper or in your mind.
Richard Feynman once wrote that he would keep four or five problems active in the back of his mind. Whenever he heard a new strategy or technique, he would quickly run through his problems and see if he could use it to solve one of his problems. He credits this practice for some of the anecdotes that gave Feynman such a reputation for being a genius. It’s further evidence that being a genius is an awful lot about effort, preparation, and being comfortable with challenges.
Subscribe for news, tips and advice from AoPS
Richard rusczyk, related articles, how to write a math solution, math contest guide for advanced students, aops summer mathwalk challenge, more articles, alcumus: a peek under the hood of our adaptive learning tool, can creativity be taught with catherine thimmesh, what’s next after beast academy, why everyone should study mathematics, learning stem through fiction, with dr. pamela cosman, embedding stem into your every day, with emily hunt, more episodes, sapienship, with dr. jim clarke, wonder, with dr. frank keil, managing academic expectations, with charlene wang, edtech at-home, with monica burns, learned helplessness, with vida john, receive weekly podcast summaries right to your inbox, get weekly podcast summaries/takeaways.
By clicking this button, I consent to receiving AoPS communications, and confirm that I am over 13, or under 13 and already a member of the Art of Problem Solving community. View our Privacy Policy .

Aops programs
7 of the hardest problems in mathematics that have been solved
Mathematics is full of problems, some of which have been solved and others that haven’t. here, we focus on 7 of the hardest problems that have been solved..
Tejasri Gururaj

What are the hardest problems in math that have already been solved?
intararit
- Some problems in mathematics have taken centuries to be solved, due to their complexity.
- Although there are some complex math problems that still elude solutions, others have now been solved.
- Here are 7 of the hardest math problems ever solved.
Some mathematical problems are challenging even for the most accomplished mathematicians.
From the Poincaré conjecture to Fermat’s last theorem , here we take a look at some of the most challenging math problems ever solved.
1. Poincaré conjecture
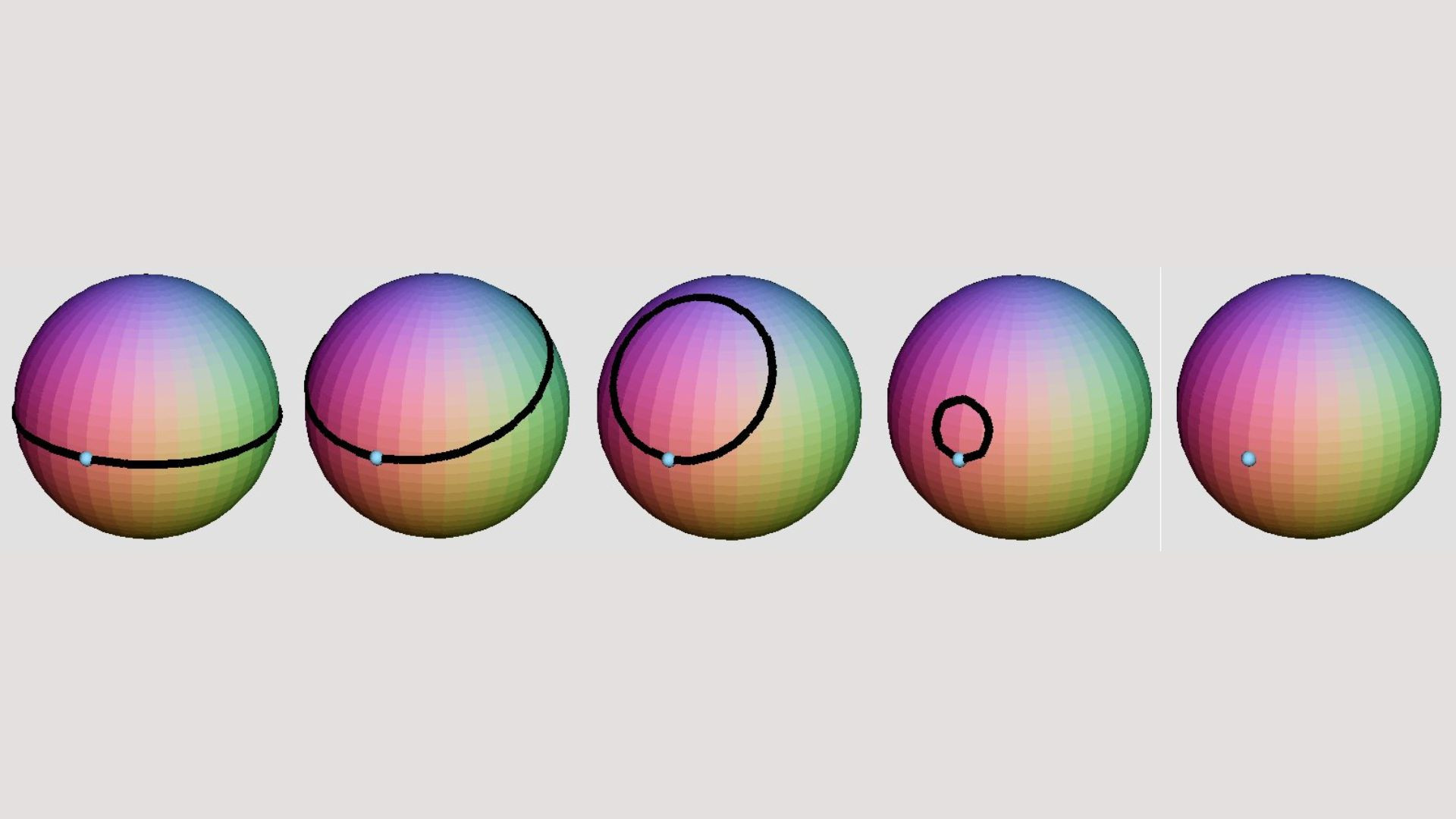
Salix alba
The Poincaré conjecture is a famous problem in topology, initially proposed by French mathematician and theoretical physicist Henri Poincaré in 1904. It asserts that every simply connected, closed 3-manifold is topologically homeomorphic (a function that is a one-to-one mapping between sets such that both the function and its inverse are continuous) to a 3-dimensional sphere.
In simpler terms, the conjecture asserts that a particular group of three-dimensional shapes can be continuously transformed into a sphere without any gaps or holes.
The problem was solved by the reclusive Russian mathematician Grigori Perelman in 2003. He built upon the work of American mathematician Richard S. Hamilton’s program involving the Ricci flow.
What makes this achievement even more remarkable is that Perelman declined the prestigious Fields Medal and the Clay Millennium Prize reward that came with it. He chose to stay away from the spotlight and mathematical acclaim, but his proof withstood rigorous scrutiny from the mathematical community.
The resolution of the Poincaré conjecture confirmed the fundamental role of topology in understanding the shape and structure of spaces, impacting fields like geometry and manifold theory.
2. The prime number theorem
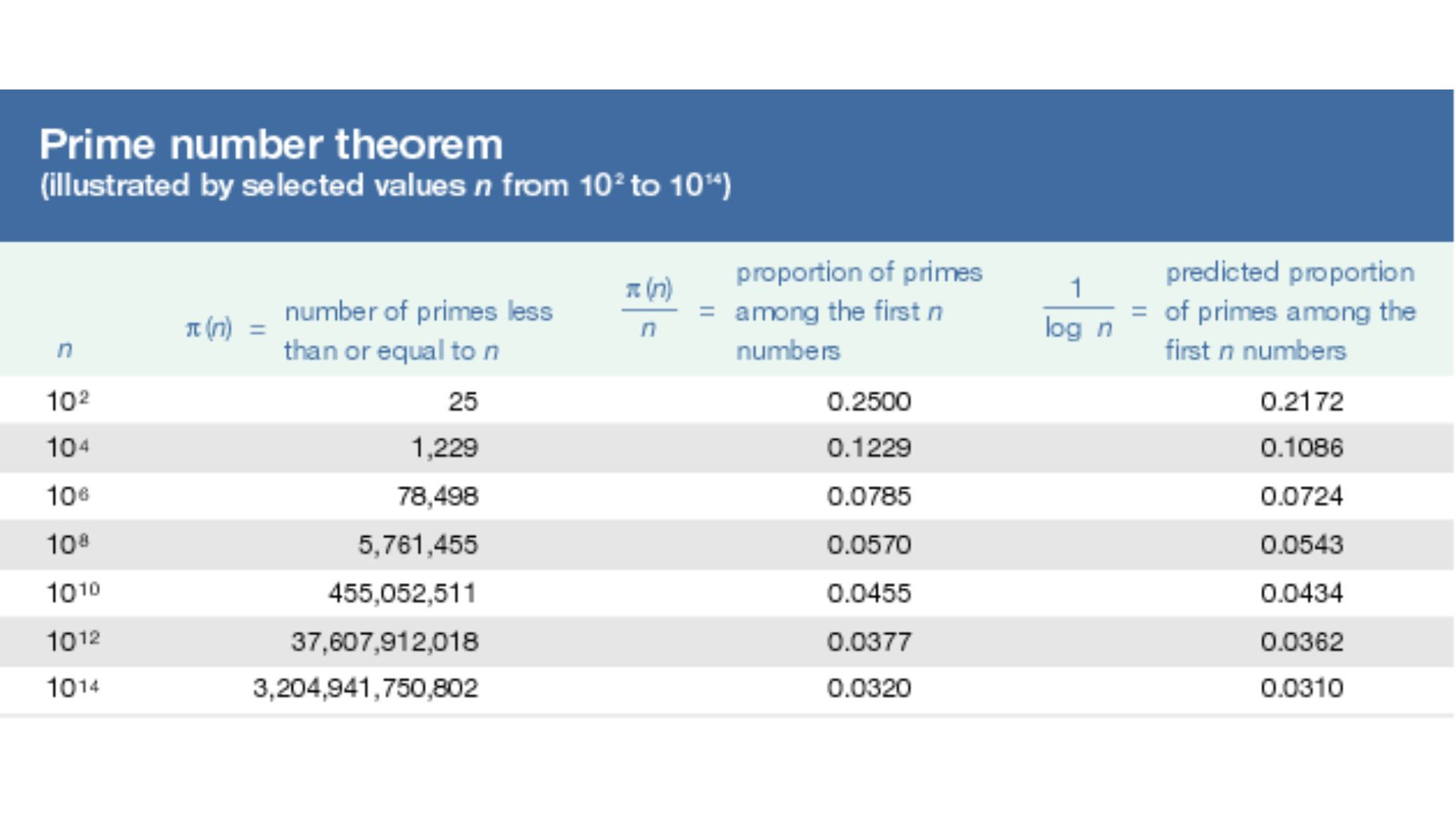
Britannica
The prime number theorem long stood as one of the fundamental questions in number theory. At its core, this problem is concerned with unraveling the distribution of prime numbers.
The question at hand revolves around the distribution pattern of these primes within the realm of natural numbers. Are there any discernible patterns governing the distribution of prime numbers, or do they appear to be entirely random? The theorem states that for large values of x, π(x) is approximately equal to x/ln(x).
The breakthrough in solving this theorem came in the late 19th century, thanks to the independent work of two mathematicians, Jacques Hadamard and Charles de la Vallée-Poussin. In 1896, both mathematicians presented their proofs of the theorem.
Their work demonstrated that prime numbers exhibit a remarkable, asymptotic distribution pattern . Their solution produced the insight that, as one considers larger and larger numbers, the density of prime numbers diminishes.
The theorem precisely characterized the rate of this decrease, showing that prime numbers become less frequent as we move along the number line. It’s as if they gradually thin out, although they never entirely vanish.
The prime number theorem was a turning point in the study of number theory . It provided profound insights into the distribution of prime numbers and put to rest the notion that there might exist a formula predicting each prime number.
Instead, it proposed a probabilistic approach to understanding the distribution of prime numbers. The theorem’s significance extends into various mathematical fields, especially in cryptography, where the properties of prime numbers play a pivotal role in securing communications.

3. Fermat’s last theorem
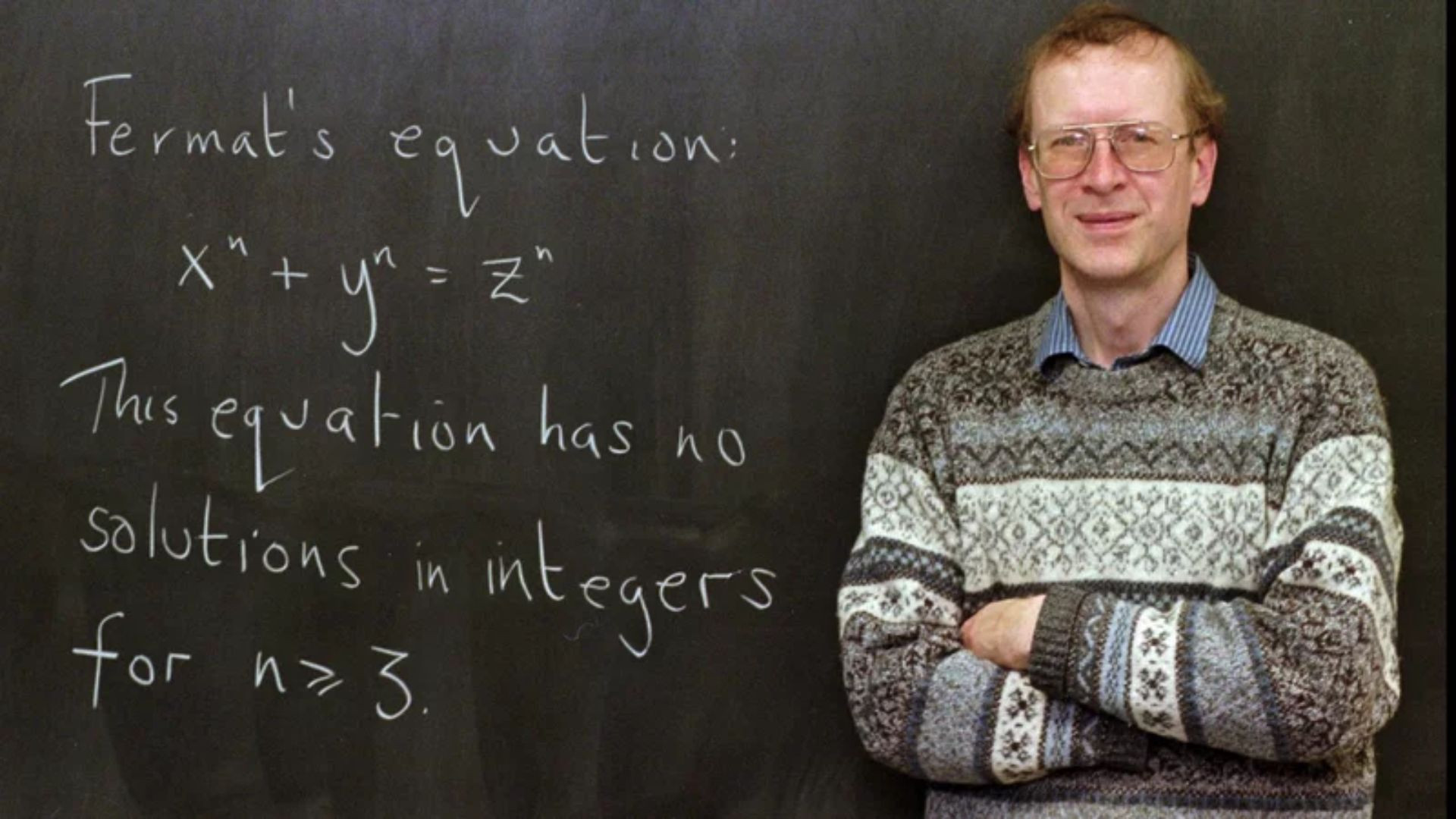
Charles Rex Arbogast/AP via NPR
Fermat’s last theorem is one of the problems on this list many people are most likely to have heard of. The conjecture, proposed by French mathematician Pierre de Fermat in the 17th century, states that it’s impossible to find three positive integers, a, b, and c, that can satisfy the equation a n + b n = c n for any integer value of n greater than 2.
For instance, there are no whole number values of a, b, and c that can make 3 3 + 4 3 = 5 3 true.
This problem remained unsolved for centuries and became one of the most challenging problems in mathematics. It was made more enticing because Fermat apparently wrote a note in his copy of the Arithmetica by Diophantus of Alexandria, saying, “I have discovered a truly remarkable proof [of this theorem], but this margin is too small to contain it.”
Numerous mathematicians attempted to prove or disprove Fermat’s conjecture, but it wasn’t until 1994 that the breakthrough came.
The solution was achieved by British mathematician Andrew Wiles, who built upon the work of many other mathematicians who had contributed to the field of number theory. Wiles’ proof was extraordinarily complex and required intricate mathematical concepts and theorems, particularly those related to elliptic curves and modular forms.
Wiles’ remarkable proof of Fermat’s last theorem confirmed that the conjecture was indeed true. Having taken more than three centuries to be solved, it had a profound impact on the world of mathematics, demonstrating the power of advanced mathematical techniques in solving long-standing problems.

Z. Ziegler, M. Ondrachek
Before Wiles presented its proof, it was in the Guinness Book of World Records as the “most difficult mathematical problem,” in part because the theorem has seen the greatest number of unsuccessful proofs.
4. Classification of finite simple groups
Jakob.scholbach/Pbroks13
This one is a bit different from the others on the list. The classification of finite simple groups , also known as the “enormous theorem,” set out to classify all finite simple groups, which are the fundamental building blocks of group theory.
Finite simple groups are those groups that cannot be divided into smaller non-trivial normal subgroups. The goal was to understand and categorize all the different types of finite simple groups that exist.
The solution to this problem is not straightforward. The proof is a collaborative effort by hundreds of mathematicians covering tens of thousands of pages in hundreds of journal articles published between 1955 and 2004.
It is one of the most extensive mathematical proofs ever produced and marks a monumental achievement in group theory.
The proof outlines the structure of finite simple groups and demonstrates that they can be classified into several specific categories. This achievement paved the way for a deeper understanding of group theory and its applications in various mathematical fields.
5. The four color theorem

Inductiveload
The four color theorem tackles an intriguing question related to topology and stands as one of the first significant theorems proved by a computer.
It states that any map in a plane can be colored using four colors so that no two adjacent regions share the same color while using the fewest possible colors. Adjacent, in this context, means that two regions share a common boundary curve segment, not merely a corner where three or more regions meet.
The theorem doesn’t focus on the artistic aspect of map coloring but rather on the fundamental mathematical principles that underlie it.
The solution to this theorem arrived in 1976, thanks to the combined efforts of mathematicians Kenneth Appel and Wolfgang Haken. However, the proof was not widely accepted due to the infeasibility of checking it by hand.
Appel and Haken’s achievement confirmed that any map, regardless of its complexity, can be colored with just four colors such that no two neighboring regions share the same color. While the idea seems simple, proving it rigorously was complex and time-consuming.
To address any lingering skepticism about the Appel–Haken proof, a more accessible proof using similar principles and still utilizing computer assistance was presented in 1997 by Robertson, Sanders, Seymour, and Thomas.
Additionally, in 2005, Georges Gonthier achieved a proof of the theorem using general-purpose theorem-proving software, reinforcing the credibility of the four color theorem.
This theorem is not actually used in map-making but has far-reaching implications in various fields, from graph theory to computer science, where it finds applications in scheduling, circuit design, and optimization problems.
6. Gödel’s incompleteness theorems

Andrew Das Arulsamy/Research Gate
Gödel’s incompleteness theorems , formulated by Austrian mathematician Kurt Gödel in the 20th century, delve into the mysteries of formal systems and their inherent limitations.
In mathematics, a formal system has a structured and well-defined framework or language that comprises a set of symbols, rules, and axioms employed for representing and manipulating mathematical or logical expressions.
Gödel’s first incompleteness theorem explores a fundamental question: In any consistent formal system, are there true mathematical statements that are undecidable within that system? In other words, do statements exist that cannot be proven as either true or false using the rules and axioms of that system?
The second incompleteness theorem takes this further: Can any consistent formal system prove its own consistency?
Gödel not only posed these questions but also provided the answers. He established, through rigorous mathematical proofs , that there exist true statements within formal systems that cannot be proven within those very systems.
In essence, the first theorem asserts that there are statements that cannot be proven as either true or false using the rules and axioms of a system. The second theorem demonstrates that no consistent formal system can prove its own consistency.
Gödel’s theorems introduced a profound paradox within the realm of mathematical logic: There are truths that exist beyond the reach of formal proofs, and there are limits to what can be achieved through mathematical systems alone.
Gödel’s contributions to mathematical logic influenced the philosophy of mathematics and our understanding of the inherent limits of formal systems.
7. The goat problem
Mnchnstnr
The goat problem is a much more recently solved mathematical problem. It involves calculating the grazing area for a tethered goat. Despite its initial simplicity, mathematicians have pondered this problem for over a century.
In its basic form, a goat on a rope can graze in a semicircle with an area of A = 1/2πr 2 , where r is the rope’s length. However, the problem becomes more complex when you change the shape of the area the goat can access.
For instance, when tethered to a square barn, the goat can access more than just a semicircle. The goat can also go around the corners of the barn, creating additional quarter circles.
Mathematician Ingo Ullisch recently unraveled the goat grazing problem, introducing complex analysis into the equation. However, the solution is far from elementary.
It involves intricate calculations, relying on the ratio of contour integral expressions and involves numerous trigonometric terms . Although the solution may not offer a practical guide for goat owners, it represents a significant achievement in the world of mathematics.
RECOMMENDED ARTICLES
What makes the goat problem truly fascinating is its capacity to act as a mathematical Rosetta stone , transcending boundaries between various fields and serving as a versatile challenge for experts from diverse disciplines.
From age-old conundrums that took centuries to crack to enigmas that continue to elude solutions, mathematical mysteries remind us that the pursuit of knowledge is an ever-evolving journey.
So, the next time you find yourself pondering a difficult math problem, remember that you are in good company, following in the footsteps of the greatest mathematical explorers!
The Blueprint Daily
Stay up-to-date on engineering, tech, space, and science news with The Blueprint.
By clicking sign up, you confirm that you accept this site's Terms of Use and Privacy Policy
ABOUT THE EDITOR
Tejasri Gururaj Tejasri is a versatile Science Writer & Communicator, leveraging her expertise from an MS in Physics to make science accessible to all. In her spare time, she enjoys spending quality time with her cats, indulging in TV shows, and rejuvenating through naps.
POPULAR ARTICLES
World’s oldest map dating back 3,000 years reveals details beyond babylonian empire, magnetic aluminum keyboards at ifa 2024, ai: can machines truly think, china’s longi sets world record for highest tandem solar cell efficiency at 34.6%, related articles.

China’s nuclear submarine sightings in Taiwan Strait show advanced tech: Report

Keiler: Rheinmetall’s breaching demon can demine hostile land within mins

Lavaforming: Using volcanic eruptions for sustainable building materials

Napoleon’s last stand: Unearthed trench reveals gruesome aftermath of Waterloo
- SAT BootCamp
- SAT MasterClass
- SAT Private Tutoring
- SAT Proctored Practice Test
- ACT Private Tutoring
- Academic Subjects
- College Essay Workshop
- Academic Writing Workshop
- AP English FRQ BootCamp
- 1:1 College Essay Help
- Online Instruction
- Free Resources
Hardest SAT Math Problems (updated for Digital SAT)
Bonus Material: The Hardest SAT Math Problems Quiz
Aiming for a really great score on the SAT? Wondering if your math skills are up to the challenge of the hardest problems?
If you want to be able to get a perfect score, you have to be able to solve the hardest SAT math problems.
We used our extensive test-prep experience to find the questions that many students miss. The examples below are real problems from past official SATs.
Give each of these 16 hard math problems a try, then read our step-by-step explanations to see if you’re solving them correctly.
If you’re thinking about getting SAT tutoring to help you tackle problems like these on the real SAT, be sure to check out our list of the 15 best SAT Tutoring Services
Then, download this quiz with 20 more of the hardest real SAT problems ever to see if you’re on track for a perfect score!

Bonus Material: 20 of the All-Time Hardest SAT Math Problems
Math on the SAT
Math accounts for half of your Total SAT Score, regardless of whether you’re taking the old paper SAT or the new Digital SAT.
On the traditional, paper SAT (which will be phased out in early 2024), the Math section comprises section 3, which contains 20 questions, is 25 minutes long and does not allow you to use a calculator; and section 4, which contains 38 questions, is 55 minutes long and does allow a calculator.
On the upcoming digital SAT (which will come into place in spring of 2024), the format is considerably different. You’ll be given two 35-minute “modules” with 22 questions in each, with the difficulty level of the second one depending on your performance on the first one. In other words, if you do really poorly on the first set of 22 questions, the second set will be easier–but your overall math score will be negatively affected. You can use your calculator on both.
Every SAT covers the following math material:
Heart of Algebra: 33% of test . Linear equations and inequalities and their graphs and systems.
Problem Solving and Data Analysis: 29% of test . Ratios, proportions, percentages, and units; analyzing graphical data, probabilities, and statistics.
Passport to Advanced Math: 28% of test . Identifying and creating equivalent expressions; quadratic and nonlinear equations/functions and their graphs.
Additional Topics in Math: 10% of test . A wide variety of topics, including geometry, trigonometry, radians and the unit circle, and complex numbers.

On the old SAT , open-ended questions came at the end of each Math section. Many students find them harder because you can’t guess or work backwards from multiple-choice options.
However, what many students don’t know is that the first 1–3 of these grid-in questions will actually be easier than the last few multiple-choice questions.
That’s because the math questions on the SAT get increasingly difficult over the course of each section, but the difficulty level starts over again with the grid-in questions.
The savvy student will know this and skip the harder multiple-choice questions to go answer the easier grid-in questions first. Of course, if you’re aiming for a perfect score, (on most tests) you’ll have to answer every question correctly .
But on the new Digital SAT, these open-ended questions will pop up at different points throughout both modules. You may see them in the beginning, the middle, or the end: there’s no set place for these to appear. Nor is there a set difficulty: generally, we’ve seen these questions be slightly on the easier side, but this varies significantly from test to test.
Because there’s obviously no bubble sheet on the digital SAT, you’ll simply type your answer into the text box. Be sure to look for instructions in the question about how they want the answer formatted!
To work with us for one-on-one tutoring or for our group SAT classes, schedule a free consultation with our team .
Why these problems are essential if you’re aiming at a top school
A perfect score on the SAT Math is 800. The only way to get this score is to answer every question correctly .
In order to score a 750, you can only miss 2 or 3 questions across both math sections .
A 750 Math SAT may sound like a very high score—and it is! It’s a very high score.

But at the very best schools in the US, three quarters of the students scored a 750 Math or better.
In fact, at the Ivy League and other top schools, at least a quarter of the students had a perfect score!
The average math scores are even higher at the top engineering schools. Three quarters of the students at CalTech had a 790 or 800, and three quarters of the students at MIT had at least a 780.
In order to be a competitive applicant to these schools, your SAT Math score should be within the “middle 50%” of the students at that school—in other words, more or less an average score for that school.
So if you’re aiming at an Ivy or one of the other top schools, you can only miss 2 or 3 questions out of the 58 math questions on the whole SAT.
If that’s your goal, make sure that you understand the problems explained below, and then try our quiz of 20 more real SAT questions that rank among the hardest questions ever.
SAT Problem #1

At first glance, this looks like a geometry question, since it talks about planes and lines and points . But this is actually an algebra question, dressed up with some geometric trappings.
The key is to realize:
1) We don’t need to solve for p and r individually. We just need to solve for (r/p) .
2) The points themselves (p,r) and (2p, 5r) represent X and Y values on the line itself. (For example if p = 2 and r = 3 then that’s the same thing as an x-coordinate of 2 and a y-coordinate of 3.)
So let’s take a look at it.
First, let’s plug in the p and r points for the x and y values to see what equations we end up with.
y = x + b becomes r = p + b
y = 2x + b becomes 5r = 2(2p) + b or 5r = 4p + b
At this point we might get a little anxious because we have three variables.
But we have to remember we don’t need to get the value of the individual letters, just the value of the relationship between r and p.
That’s where b actually becomes helpful. Because we can now set both equations equal to b , plug in, and then see if we can manipulate the r and p to get them to express the same relationship we want.

So, first set both equations equal to b to get:
b = r – p
b = 5r – 4p
And since, obviously b = b …
r – p = 5r – 4p
Let’s now use some basic algebra to put the like variables together, so:
Now we’re nearly home. All we have to do is manipulate the problem so r/p .
So, divide both sides by 3p :
4r / 3p = 1
Then multiply both sides by 3:
And finally divide by 4, which gives us:
CHOICE B
Download the Hard SAT Math Problems quiz
SAT Problem #2

This is a question that can cause all sorts of problems if you forget your exponent rules—but it’s otherwise very straightforward.
So let’s go over a few of those rules, just to get comfortable . . . and notice a pattern. I’ve included three below:
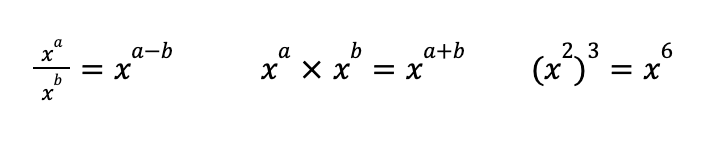
Two things to pay attention to:
First, when we divide variables with exponents, we keep the base and subtract the exponent. When we multiply variables with exponents, we keep the base and add the exponents. When we take a variable with an exponent to an additional power, we multiply the exponents.
Second, in order to use the first two of these rules, the two numbers must have the same base .
There is a base x on both the top and bottom of that fraction or the left and right side of that multiplication sign.
So how does that help us here?
Let’s forget the first half of the problem and look at the second:
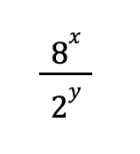
We might look back at these exponent rules and throw our hands up—the top and bottom parts of this fraction don’t have the same base, so what am I supposed to do here?
Except…
8 and 2 actually DO have the same base. Base 2.
Isn’t 2^3 equal to 8?
So if we re-write the problem, plugging in 2^3 for 8, and thinking about that third exponent rule I gave you above, the equation will look like this:
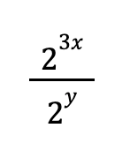
Now let’s go back to our exponent rules once more, and look at the first one.
Because that tells us that…
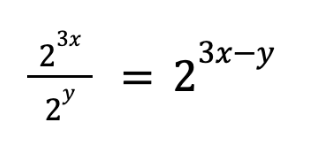
Well, hold on a second!
We know the value of 3x – y .
The problem tells us it’s 12.
So we just plug in and get our answer…
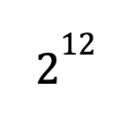
Which is CHOICE A.

Keep up the practice! If you’d like help honing your skills, reach out to us for a free test prep consultation. All of our tutors are top 1% scorers who attended top-tier schools like Harvard and Princeton. That makes them uniquely qualified to help high-scoring students improve.
SAT Problem #3
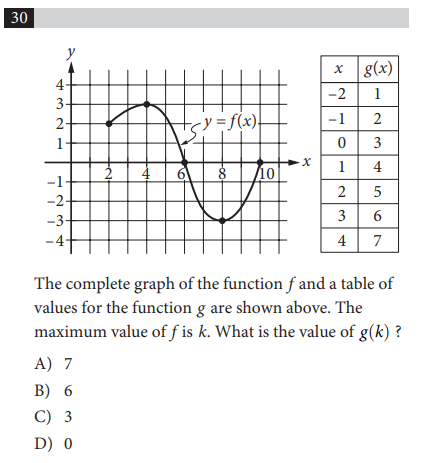
A question like this confuses a lot of students because they either forget how minimums and maximums work or find it hard to keep track of which numbers they are plugging in and where.
In order to solve it, it’s helpful to think of a function as a machine . We enter an input into the machine (an x value)—it acts on it—and then it gives us an output (a y value).
Let’s also remember that when we’re talking about minimum and maximums we’re talking about the y value when the function is at its highest and lowest point .
With these two facts in mind, the problem is going to be much simpler, so let’s take it on in parts…
Since the question is asking us for g(k) and k represents the maximum value of f , it’s going to be helpful to first…
Find k .
So what is the maximum value of f , the graphed function? Well, the maximum value (as we realized earlier) is the y value when the function is at its highest.
Looking at the graph, it looks the function is at highest when x = 4 , and more importantly, when
Therefore, k = 3 .

Now let’s consider our functions as machines.
When the problem asks us for g(k) , it’s telling us that k is going to act as the input (the x value for the function). So g(k) , the value after the machine acts upon the function, is going to be the output , or the y value .
So, g(k) is the same as g(x) , except we’re plugging in our value of k , which is 3, for our x value.
The rest is very simple.
We go to the table and find where x = 3 , then move our finger across to see the output for that value, which is 6.
CHOICE B.
Test your SAT math knowledge with our quiz
SAT Problem #4
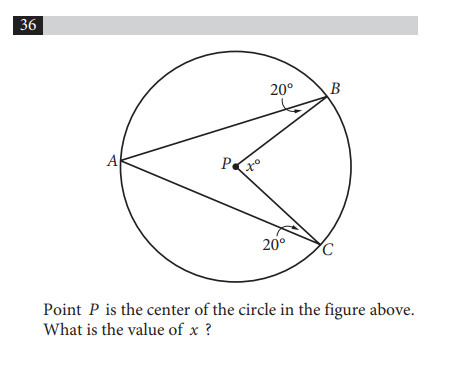
A version of this question has appeared on the SAT multiple times in recent years, and it often stumps students!
Here we have something that resembles a rotated version of the logo from Star Trek, and we’re asked to find the value of a degree inside the circle, between two points of the pointed figure.
We’re given a point that represents the center of the circle, along with two degree measurements inside the triangle-like figure.
Generally, when we’re given a figure that looks unfamiliar to us—like the figure inside the circle— it can be extremely helpful to find a way to fix it (or cut it up) so that it’s made up of parts of shapes that are more familiar .
So looking inside this circle, how might we “fix” this figure so that it becomes a little friendlier.

Well, if we draw a line to the center of the circle ( P ) from the edge of the circle ( A ), then this unfamiliar figure suddenly becomes two triangles.
And with triangles, unlike the figure we were originally given, we can apply some rules .
Rules, for example, that dictate opposite sides of the triangle that have the same length will have the same opposite angles.
And if we look at our drawing we see that two sides of our triangle are the same length because they’re both the radius …
And so we also know that the opposite angles of those sides will be the same…
And we’ve been given one of those angles!
Therefore, angles ⦣ABP and ⦣PAB will be the same—both 20 degrees. Let’s fill that in.
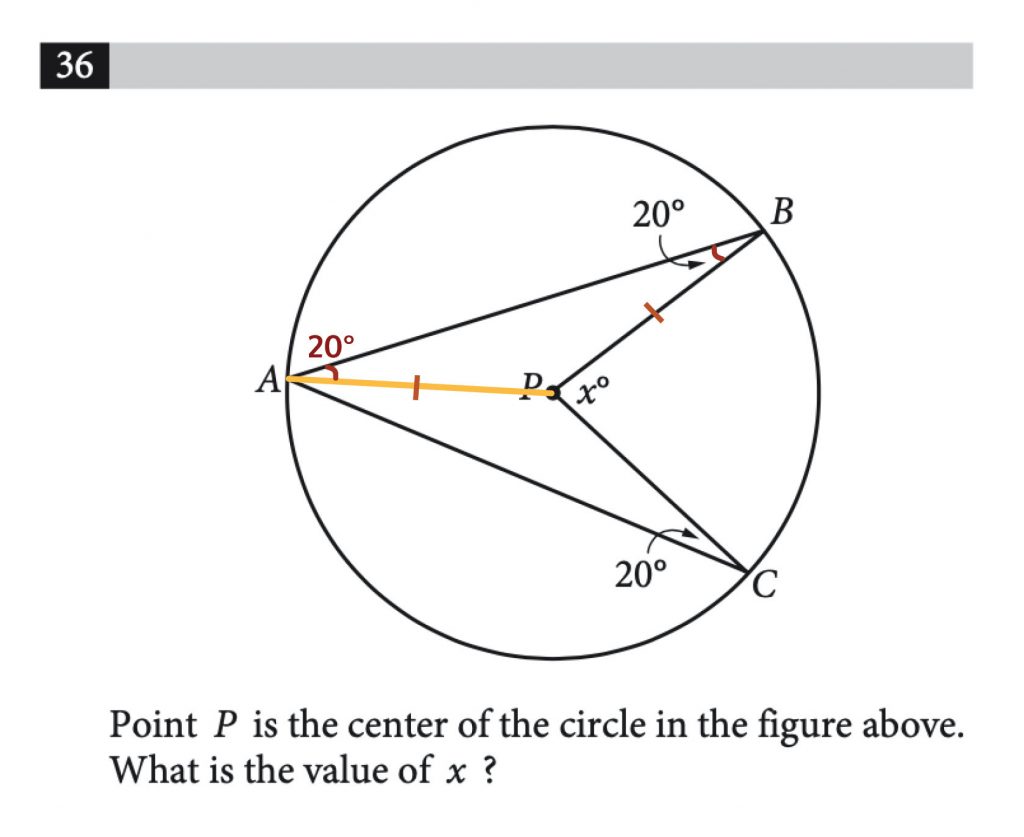
Now again—because we have a triangle—we can apply another rule as well.
We know that degrees of a triangle will add up to 180 degrees.
So if we know one of the inner degrees of the triangle is 20, and the other is 20—the remaining angle has to be 140 degrees. (Because 180 – 40 = 140. )
We have two of these triangles, so we know the larger inner angles of both add up to 280.
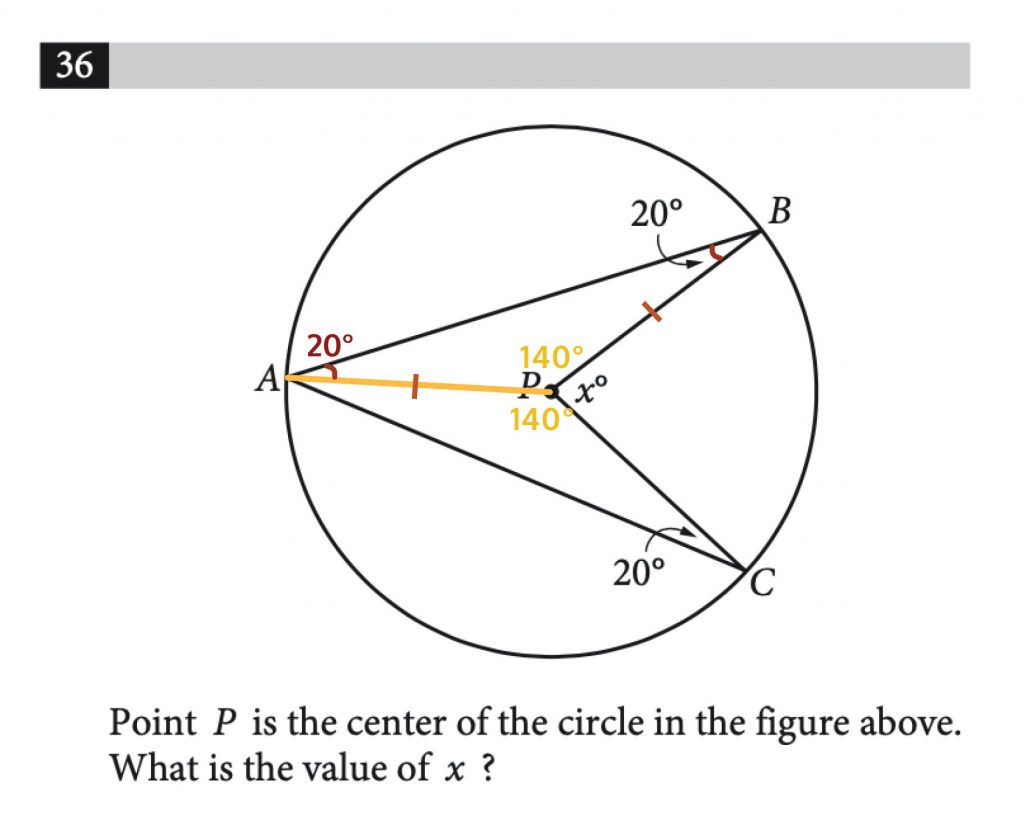
Because a circle is 360 degrees, the number of degrees “left over” when 280 is subtracted from 360 is 80.
So X equals 80.

There is actually a second clever way to solve this problem, involving arc measures. Can you spot it? (If not, don’t worry! Ask us how we did it here .)
SAT Problem #5

Here we have a problem that looks quite complicated—and one I find students often waste a lot of time on. They either try to plug in answers and work backwards…
…or they waste time trying to combine the two terms on the right side of the equation and simplifying.
It turns out the easiest way to solve this problem is by polynomial division , because we’ve already been given the answer! It’s the right-hand side of the equation: (-8x – 3) – (53 / (ax – 2)) .
That means that this is our answer to when (24x^2 + 25x – 47) is divided by ax – 2 .
So how does that help us get a value for a ?
Well, let’s set this up as a polynomial division problem.
We’d write it as follows:
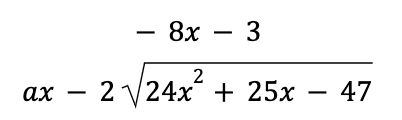
(I’m not putting the second half of the right side of the equation on top because that’s going to be our remainder.)
So now we have a simple question. What number divided into 24 , gives me -8 ?
Well, that’s easy. It’s -3 , right?
Because -3 * -8 gives me 24 .
So a equals -3 , CHOICE B .
Now, you could spend time plugging in -3 for a and dividing through the rest of the problem to make sure your answer matches the one on the exam—but generally on a timed test you really shouldn’t do more work than necessary.
In fact, by setting this up as a polynomial division problem, we’ve saved time precisely because we don’t have to complete all the work . . . just enough to get us our answer.
Try the quiz
SAT Problem #6

Because the SAT is a timed test, “difficult” includes not only questions that are hard to solve, but also those that—if a few wrong decisions are made—take a long time to solve.
Sure, you may get the right answer, but those extra seconds or minutes wasted will inevitably cost you on other questions later on the exam.
Generally speaking, you should be able to answer each question in about a minute. If you spend more than 60 seconds on a single question, you should put down your best guess and move on (and hope that you have extra time at the end to return to this question).
To that end, let’s look at this question. You’re asked to find the value of 3x – 2 , and you’re given this equation:
(⅔)(9x – 6) – 4 = (9x – 6)
Many students will immediately think: “This is totally straightforward: Solve for x and plug it back into the equation.”
They’ll distribute the ⅔ and end up with something like this:
6x – 4 – 4 = 9x – 6
and then go through all the algebra from there, to get… 3x = -2 .
These students will then find that x = (-⅔) .
A few unlucky students will then forget that they have to plug in, and they’ll choose the trap answer C.
The lucky ones will plug the (-⅔) back into 3x – 2 and get the correct answer, -4 , A .
However, it turns out there is actually a much quicker way to solve this problem!
We can solve it without ever having to plug into a second equation.
If we simply subtract (⅔)(9x-6) from both sides, we end up with…
-4 = (⅓)(9x-6) .
We can realize that (⅓) of 9x-6 is the same as 3x-2 .
And, what do you know…
-4 = 3x – 2 .

Ready to try some of these problems on your own? Try our quiz with 20 more of the hardest real SAT problems ever to see if you could get a perfect score on the SAT Math!
SAT Problem #7

This is a question you could muscle through, but it’s going to be a lot easier if we find a few shortcuts and work from there. Remember, a hard question isn’t necessarily difficult because of the conceptual and mathematical effort it asks from you but also because of the time it might require.
So how do we save ourselves some time?
First, let’s notice that in the answer choices none of these numbers repeat . There are eight distinct numbers in the answer choices. Therefore, if we were pressed for time we only really have to find one of the values of c , choose the corresponding answer choice, and then move on.
Second, let’s look at the other piece of information this problem gives us besides the quadratic.
It tell us that a + b = 8.
This should be especially helpful because we know from FOIL (and what the rest of the problem gives us) that a * b = 15 , because abx^2 is going to be equal to 15x^2.
Because a + b = 8 and ab = 15 , we know that the values of a and b are going to be 3 and 5.
(We don’t know which one is which, and that’s precisely why this problem has two possible values for c .)
At this point we’ve done most of the “hard” work to save time in this problem, and it hasn’t even been particularly hard!
Now all we have to do is assign one of 3 or 5 to a , assign the other to b , FOIL out the problem, and pick whichever choice corresponds to one of the values of c .
Let’s say a = 3 and b = 5 .
It will work like this:
(3x + 2)(5x + 7) = 15x^2 + 21x + 10x + 14 .
Which simplifies to…
15x^2 + 31x + 14 .
Which means c = 31 .
31 only appears once in our answer choices, so the answer must be CHOICE D.
SAT Problem #8

When you’re faced with one of these more difficult system-of-equations problems—specifically the ones that ask you for no solutions or infinite solutions —it’s going to be much, much easier to think about the problems geometrically.
In other words, as two line equations.
So what does it mean for two lines to have no solutions ?
Well, for two lines to have no solutions, they’d have to never intersect , correct?
(Just like if one of these problems asks you about two lines with infinite solutions , they’re saying that the lines are the same . They’re laid on top of each other. )
In other words, they’d have to be… parallel lines .
And parallel lines have the same… slope!
So this question is asking you to find the correct value for the variable that gives these lines the equivalent slope .
Obviously, the first step is to put both of these equations in slope-intercept form. We’d end up with:
y = (-a/2)x + 2
Now the rest is very simple. All we need is a value of a that makes the slopes equal, so that it solves the equation (-a/2) = 3 .
With some basic algebra, we end up with -a = 6 . This is the same as a = -6 .
So the answer is CHOICE A, -6.

Are these problems feeling super hard for you? Want to work on more similar problems? Check out our one-on-one tutoring with Ivy-League instructors. A great experienced tutor can help you focus on the concepts that are the hardest for you until you understand them thoroughly.
SAT Problem 9

This is another type of problem that students often have conceptual difficulty with, causing them to waste much more time than they should.
(Remember, basically every problem in the SAT math section is designed to be solved in a minute and half or less. If you’re taking three or four minutes on a math problem, you’ve probably made a mistake!)
Some students will see that (u-t) is defined but not u or t individually, so they’ll try either solving for u in terms of t (or vice versa), or they’ll try squaring (u-t) to get a solution. (Which is closer to the correct way to solve the problem, but still incorrect).
Instead, to solve this problem we need to remember the difference of squares .
Remember, that the difference of squares states the following…
(x+y)(x-y) = x^2 – xy + xy – y^2 .
Which means…
(x+y)(x-y) = x^2 – y^2 .
And doesn’t that look awfully familiar to… u^2 – t^2 ?
In fact, we can now replace u^2 – t^2 with (u + t)(u – t) .
So the whole problem would now read: (u + t)(u – t)(u – t) . Since we know the value of (u + t) and (u – t) , this would simply be the same as (2)(5)(2) .
Which equals our answer…
Ready to see how you’re doing? Download the quiz
SAT Problem #10

What makes this question confusing is that students often get thrown off by the repetition of the (⅓).
They forget that when the ⅓ gets factored out of the parenthesis like that, it means it’s going to apply to the whole equation: both the x^2 AND the -2 .
Once we remember that, we can solve this problem by difference of squares . This will save us the time of having to brute force the answer choices and FOIL each one through for the different values of k.
We’ll simply square k and subtract it from the x^2 for each choice.
That will give us the following four choices:
(⅓)(x^2 – 4)
(⅓)(x^2 – 36)
(⅓)(x^2 – 2)
(⅓) (x^2 – 6)
A student might rush to choose the third answer choice, since it appears to look like the expression at the beginning of the problem, but remember what I told you at the beginning:
We’re going to apply that ⅓ to both the x^2 AND the k !
If we multiply that ⅓ through, the choices suddenly look like this…
(⅓)(x^2) – (4/3)
(⅓)(x^2) – (12)
(⅓)(x^2) – (⅔)
(⅓)(x^2) – (2)
. . . and so the correct answer is actually the fourth choice, CHOICE D .

Ready to try more hard problems on your own? Download our free quiz to try 20 more of the hardest ever (real) SAT problems.
SAT Problem #11

There are not many problems on the SAT that involve knowing the equation for a circle—in fact, circle equation problems don’t show up on every test—but that’s precisely why students often find a problem like this more difficult.
First, let’s do a quick refresher on what the numbers in the equation of a circle mean.
Any equation for a circle is going to be in this form:
(x – h)^2 + (y – k)^2 = r^2
Where h and k represent the coordinates of the center and r is the radius.
Let’s apply that to our problem here…
(x + 3)^2 + (y – 1)^2 = 25.
Remember: because in the form of the circle equation the numbers inside the parenthesis are subtracted from x and y , when they appear inside the parenthesis as positives , that indicates the coordinate point will be negative.
Therefore the center of this circle is at point (-3, 1) .
Because the radius is expressed as r^2 , then the 25 indicates the radius will be 5 .
So we have a circle centered on the point (-3,1) and with a radius of 5 .
So… now what?
How do we figure out which of these points is not inside the circle?
First, let’s draw the circle itself and look at it. On the SAT itself, you won’t have graph paper, so just draw a rough sketch!
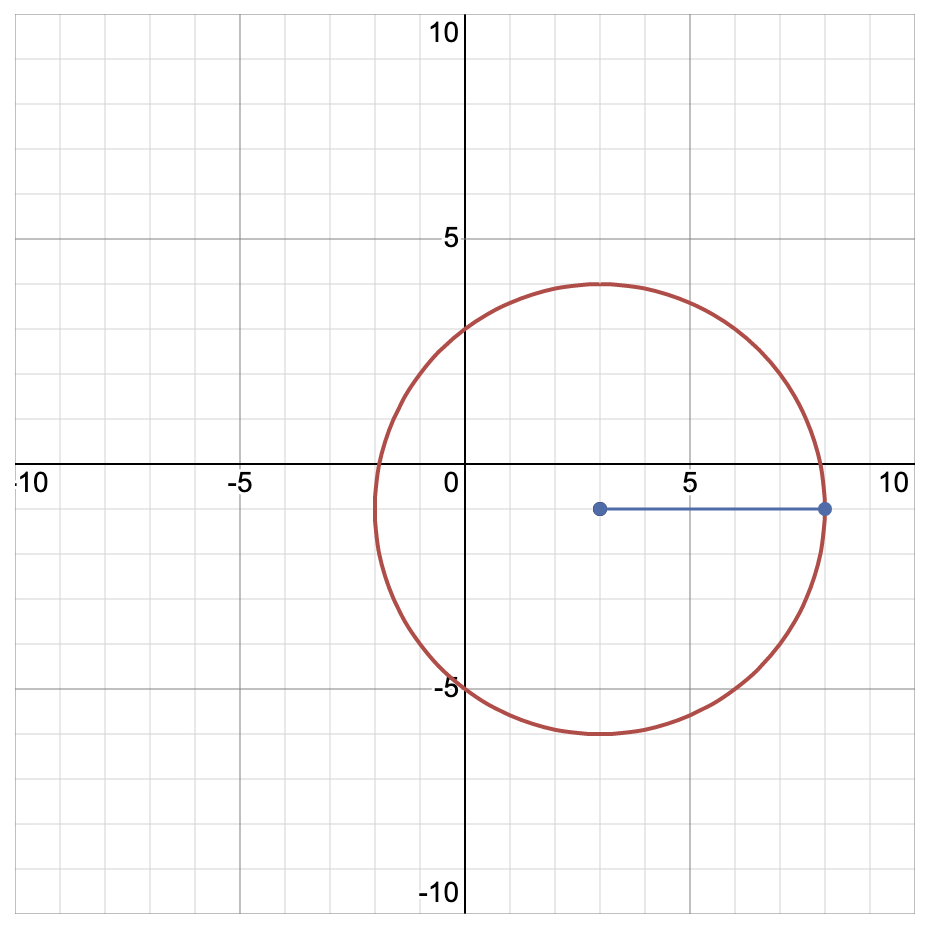
Of course if we’re truly flummoxed we could graph the points, eliminate what we can . . . and guess.
But that’s not ideal, obviously!
Instead, let’s think about what the radius means.
The radius demarcates the boundaries of the circle from the center.
In other words, any points with a distance less-than-the-radius away from the center will lie within the circle.
And any points more-than-the-radius distance from the center will lie outside of it.
(Any points exactly-the-radius distance from the center will lie on the circle itself.)
So all we have to do is find the point that is more than 5 units away from our center, and that will be our answer.
To do this requires the distance formula.
Remember, the distance formula is
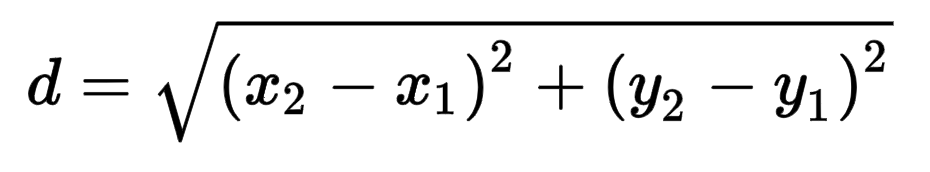
A quick note: if you ever forget the distance formula, simply plot the two points on a graph, make a triangle with the distance between the two points and the hypotenuse, and use the Pythagorean Theorem to find the length of the hypotenuse, like this:
Going back to our problem, let’s plug each of the points in along with our radius to the equation. (I’ll include the second point here, although since that’s our center we need not actually bother with it when we’re going through the problem.) We end up with:
√(-3 – (-7))^2 +(1-(3))^2) = √20
√(-3 – (-3))^2 +(1-(1))^2) = √0
√(-3 – (0))^2 +(1-(0))^2) = √10
√(-3 – (3))^2 +(1-(2))^2) = √37
Only the square root of 37—choice D—is an answer that is larger than five.
So that’s our correct choice, D .
Want more hand-picked problems? Get the quiz
SAT Problem #12
More circles! Let’s recall how the equation for a circle looked. It’s…
(x – h)^2 + (y – k)^2 = r^2
What the problem gives us, unfortunately, does not resemble that equation…
…so our goal is to get the equation in the problem to look like a normal equation for a circle.
Once we do this, we’ll just have to take the square root of whatever is on the right side of the equation, and that will give us our answer.
But how?
We need to do something called completing the square .
For the SAT, this concept is slightly obscure—it’s one you may see only once (or not at all) on a given exam. It makes the question a bit more difficult.
Completing the square is normally a process reserved for solving a quadratic equation, but if you look closely at the way this problem is set up –
2x^2 – 6x + 2y^2 + 2y = 45
we see that what we really have here are two quadratic equations, so we just have to complete the square twice.
First we have to get rid of the coefficient in front of the x and y squared, so we have to divide through by 2 .
This gives us x^2 – 3x + y^2 + y = 22.5 .
Now we’re reading to complete the square!
Let’s deal with the x terms first. We have to think of what number, if we had it here in the equation, would allow us to factor x^2 – 3x into something of the form (x – z)^2 , where z is a constant. If we think about it, we realize that z has to be half of b . In this case, that means half of -3 , so -1.5 .
When we pop that into our setup, we get (x – 1.5)^2 . If we FOIL this out, however, we see that we get x^2 – 3x + 2.25 .
So it turns out that in order to be able to rewrite our expression in the form we want, we need to add 2.25 to our equation. As always in algebra, we do the same thing to both sides, so now we have:
x^2 – 3x + 2.25 + y^2 + y = 22.5 + 2.25.
Now we do the same thing for the y terms! Again, we need to add something to the equation so that we could rewrite the y part of the expression in the form (y – z)^2 . To get this number, we take half of the b term and square it: 1 divided by 2 , then squared, so 0.5^2 or 0.25.
Again, we have to add this number to both sides of the equation. Now we’ve got:
x^2 – 3x + 2.25 + y^2 + y + 0.25 = 22.5 + 2.25 + 0.25.
We can factor and rewrite this like:
( x – 1.5)^2 + (y + 0.5)^2 = 25.
Alright, now this is finally in the right format for the equation for a circle!
The final step is to use this equation to find the radius.
We know that the equation for a circle is (x – h)^2 + (y – k)^2 = r^2 . Fortunately this works out really nicely, since 25 is just 5^2. The radius must be 5, CHOICE A .

We’ve tutored thousands of students and used that experience to assemble a list of 20 more problems that students frequently miss. Can you answer them correctly? Download the quiz now to find out!
SAT Problem #13
This question involves a number of moving parts and thus can be a little overwhelming for students to follow.
It asks us to find, based on the rotation of the first gear, the rotation of the third.
I find many students trip up on this problem by making two errors that are simple to fix, but relatively common. They fail to take the problem step by step… and they fail to write down their work as they track through the material.
With that in mind, let’s work through the problem.
Because gears A and C do not connect directly, but instead through gear B, we should first try to figure out the rotational relationship between A and B (at 100 rpm) before applying that to B and C.
Because B is larger than A (and has more gears), A is going to rotate fully multiple times before B rotates once.
How many times? Here it’s helpful to consider a ratio.
A has 20 gears.
B has 60 gears.
So A is going to have to rotate three times before B rotates once . (20 goes into 60 three times.)
Therefore, the ratio of rotation between A and B is 3 : 1 .
Let’s write that down and then apply the same method to figure out the ratio between B and C.
C has 10 gears.
Here B only has to rotate a sixth of its distance for C to rotate once, so the ratio of rotation between B and C is 1 : 6 .
Now we take the number of RPMs the problem gives us, start with the gear on the left and multiply through with our ratios.
So if Gear A rotates 100 times RPMS per minute, Gear B will rotate a third of that distance…
So we divide 100 by 3.
Because we know Gear C rotates six times as fast as Gear B, we then take our answer and multiply it by 6.
So we get (100)(⅓)(6) .
Which gives us 200 rpm.
CHOICE C.
SAT Problem #14
This question appears complicated—and students often get tripped up trying to either plug in numbers (which can be time consuming) or by searching for an equation that explains the relationship between the surface area and perimeter of the cube itself.
This is especially tempting because while the question gives us the equation for the entire surface area of the cube, it only asks for the perimeter of one of the cube’s faces.
However…
If we think about the properties of a cube, this question actually becomes quite simple.
First, let’s draw a cube.
Again, the equation the problem gives us is for the entire surface area of the cube: 6(a/4)^2 .
But when we look at the cube, we may notice that it has, in fact, six faces.
Therefore, each face would have one sixth of the surface area of the entire cube.
So by dividing the equation by six, we get the surface area for one face of the cube, which is:
But the question asks for the perimeter of one face of the cube.
Let’s examine the drawing of the cube one more time.
What shape is each cube face? It’s a square.
And because each side of a square (let’s call each side x ) is equal to the other, the area of the square is going to be x^2, or the length of the side times itself.
Well, wait a moment…
If we go back to our equation for the surface area of ONE face of the cube, (a/4)^2 , we might notice that it’s in the same form as the equation for area of the square, except instead of x being squared, it’s (a/4) .
And if we replace the x with (a/4) , we find that each side of the square is equivalent to (a/4) .
Which makes finding the perimeter of this square quite simple, because it has four sides.
So we merely add the four sides together:
(a/4) + (a/4) + (a/4) + (a/4) . . .
which equals a .
Which in this case is CHOICE B .

Want more practice? We collected 20 more of the hardest SAT math problems. Download the quiz and take it with a 25-minute timer to mimic the real test!
SAT Problem #15

We have a lot of variables in this question, so it’s easiest to try to incorporate the extra piece of information we’re given, b = c – (½) , as best we can and then try to simplify the problem and solve from there.
So how can we do that?
The problem tells us b = c – (½) , which can also be expressed as b – c = -(½) .
(Once we put the b and c together on one side, it becomes easier to replace them together with a number).
So what’s the best way to manipulate these two equations so that we’ll have b – c , which we can then replace with the (-½) and be left with x and y ?
Because let’s remember that the problem does not ask us to solve for x and y individually.
Just their relationship.
So once we’re left with x and y as our only two variables, we should be able to make good progress.
Anyhow, looking back over these two equations it seems the easiest way to be left with b – c is to…
…subtract the bottom equation from the top one.
When we do so, we’re left with the following:
(3x – 3y) + (b – c) = (5x – 5y) + (-7 – (-7))
We replace b – c with -½
And then combine like terms to get…
(-½) = (5x – 3x) – (5y + 3y)
(-½) = 2x – 2y
Divide through by 2 …
-¼ = x – y
Or x = y – (¼)
So our an answer is x = y – ¼ , CHOICE A .
Download 20 more of the hardest problems ever
SAT Problem #16

There are a few ways to solve this problem. The easiest one is simply to know the “remainder theorem.”
I don’t want to get too sidetracked with details, but remainder theorem states that when polynomial g(x) is divided by (x – a) , the remainder is g(a) .
In other words, when p(x) is divided by (x-3) here, the remainder would be p(3) , which, according to the information we’re given, is -2 .
That leads to CHOICE D .
But what if, like many students, you don’t know the remainder theorem? (It’s pretty obscure and there’s a good chance you won’t see a problem about it on the entire exam.)
Let’s look at an alternative way to solve the problem.
If p(3) equals -2 , let’s imagine a function where that might be the case.
We could do as simple one, like y = 3x – 11 , or a more complex one, like y = x^2 + 3x – 20 .
Either way, if I plug 3 into either of these functions for x , I get -2 as a y value.
I should also notice immediately that (x – 5) , (x – 2) , and (x + 2) are not factors of either of them.
Clearly choices A, B, and C are not things that must be true.
This also, by process of elimination, leads to CHOICE D.
But just to check, let’s divide x – 3 into one of these functions – say 3x – 11 – and see what happens:
The x goes into 3x three times – and three times (x-3) equals 3x – 9 .
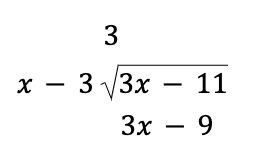
When I subtract 3x – 9 from 3x – 11 , I get -2 , which is my remainder.
Which points us, again, to CHOICE D .
Test your knowledge with 20 more problems
If these problems feel really hard, don’t panic—you can still do well on the SAT without answering every question correctly.
The average SAT Math score for US students in 2022 was 52 8, and you have to answer about 32 out of 58 math questions correctly to get this score. That’s only a little over half of the questions!

However, if you want a high score—or a perfect score—you’ll have to be able to answer tough questions like these. You’ll need a very high score to be a competitive applicant for Harvard, Stanford, MIT, or other highly competitive schools.
The good news is that it’s very possible to raise your math score!
In fact, it’s typically easier to improve your SAT Math score than your Reading & Writing score. Good preparation (on your own or with a tutor ) will fill in the knowledge gaps for any concepts that might be shaky and then practice the most common problem types until they feel easy.
We’ve worked with students who were able to see a 200-point increase on the Math section alone, through lots of hard work and practice.
To see how your math skills stack up against the toughest parts of the SAT, download our quiz with 20 more of the hardest SAT math questions, taken from real tests administered in recent years.
Once you know where you stand, keep up the practice!
If you’re interested in customized one-on-one tutoring support from an expert SAT tutor who can help you understand these tough problems, schedule a free consultation with Jessica or one of our founders . Our Ivy-League tutors are top scorers themselves who can help you with these more advanced concepts and strategies.
Bonus Material: Quiz: 20 of the All-Time Hardest SAT Math Problems

Emily graduated summa cum laude from Princeton University and holds an MA from the University of Notre Dame. She was a National Merit Scholar and has won numerous academic prizes and fellowships. A veteran of the publishing industry, she has helped professors at Harvard, Yale, and Princeton revise their books and articles. Over the last decade, Emily has successfully mentored hundreds of students in all aspects of the college admissions process, including the SAT, ACT, and college application essay.
CHECK OUT THESE RELATED POSTS

How to Write Vanderbilt’s Supplemental Essays for 2024-2025
September 4, 2024
For this application cycle, Vanderbilt only has one supplemental essay prompts, which you’ll have to answer with a maximum of …

How to Write Villanova’s Supplemental Essays for 2024-2025
For this application cycle, we’ve got good news. Although Villanova has 5 supplemental essay prompts, the word count is quite short. Plus, you’ll only have to choose…

How to Answer the Harvard Supplemental Essay Prompts (2024-2025)
September 3, 2024
What are the Harvard supplemental essay prompts for 2020-2021? And how should you respond to them successfully? We've got the answers.

How to write the Princeton supplemental essays (2024-2025)
August 28, 2024
What are the 6 Princeton supplemental essay prompts? And how should you respond to each? We answer both questions in this detailed post.

How to Write Boston College’s Supplemental Essays for 2024-2025
August 24, 2024
For this application cycle, we’ve got good news. Although Boston College has 4 supplemental essay prompts, you’ll only have to choose one. The word count for this essay…

How to Write the Dartmouth Supplemental Essays for 2024-2025
August 20, 2024
Add excerpt here. Can reuse meta description.

How to Write Yale’s Supplemental Essays (With Real Examples) 2024-2025
This application cycle, Yale’s supplemental essay set is quite intense. To help you, we’ve got detailed guides for each one, plus real Yale sample essays from previous years for…

How to Write the University of Chicago Supplemental Essays for 2024-2025
For this application cycle, University of Chicago once again has a set of unusual supplemental essay prompts. We take a look at each prompt, then analyze a real University of Chicago sample essay to…

Colleges that Require SAT/ACT Scores 2024/2025
August 7, 2024
While test-optional policies came into effect at many colleges during the pandemic, that’s now changing. Schools like Harvard, Brown, and Dartmouth …

101 Colleges with Late Deadlines
Every college has different deadlines, but most of them tend to be around the start or middle of January. But some colleges will allow you to submit applications far later, which can be an important…
Privacy Preference Center
Privacy preferences.
The Legend of Question Six: One of The Hardest Maths Problems Ever

It's a secret to no one that maths is hard , so when you start talking about the hardest maths problems ever, things start to get a little crazy. Take the innocuously named Question 6, which is so complex, it can bring mathematicians to tears.
As mathematician Simon Pampena explains the Numberphile video above , the Legend of Question 6 spawned from a maths competition for high-schoolers held in Australia in 1988. (Yep, they make 'em tough down here.)
The competition was the International Mathematical Olympiad, which is held every year in a different country, and only six kids from every country are selected to compete. Points are scored on how each 'mathlete' performs on six different questions.
In 1988, the Australian Olympiad officials decided to throw a massive curveball to the kids on the final day of competition, and it's gone down in history as one of the toughest problems out there.
Just to give you an idea of how tough it was, Australian-American mathematician Terence Tao - recipient of the 2006 Fields Medal (the mathematician's 'Nobel Prize') - scored a 1 out of 7 when he attempted it. But, you know, he was 13 at the time, so let's cut the man some slack.
What made Question 6 so hard is that it actually tried to pay mind games with you as you solved it.
"In a way, they're actually designed to kind of throw you off if you know high school maths too well," says Pampena . "So say if you really know how to solve quadratic equations, and you see something that looks like a quadratic equation, it almost throws you down the wrong path."
Question 6 was actually submitted to the Australian Olympiad officials by a mathematician from West Germany, and the officials gave themselves SIX HOURS to solve it to see if it should be included in the event.
Not one official could solve Question 6 within the time limit. Some of the best mathematicians in the world at the time.
But they put it on a test for kids anyway, and only gave them about 90 minutes to solve it, because mathematicians are ridiculous.
So you just want to know wtf this problem is, right? Okay, here it is:
Let a and b be positive integers such that ab + 1 divides a 2 + b 2 . Show that a 2 + b 2 / ab + 1 is the square of an integer.
What's the solution? Well, we're going to let the Numberphile video above explain that one to you… nope sorry, there's no way they're fitting all that into a single video.
The video above will tell you what the question actually means, and then the video below will give you the answer:
Just please don't pop a vein in your head or something if you attempt it yourself. And if you somehow crush it, here's six more to try .
38 Hard Math Riddles (With Answers) For Future Geniuses
Stump the mathletes of the family with these extra-tricky math riddles and puzzles.

No one’s indifferent to the long-form math word problem with the opening lines, “There are 67 people on a train traveling west at 45 miles an hour.” Those verbal equations tend to either thrill us or fill us with dread. While we all tumble effortlessly through daily encounters with simple arithmetic, sometimes math riddles and word problems stop us in our tracks. They’re often a thorny and delightful combination of the abstract and the real world, which is why they’re perfect for kids.
To solve a math riddle, kids must convert a few sentences about a real-life scenario into the right combination of mathematical equations. Using logic, creative problem solving, and common sense, children can crack any code, including math riddles. Although tough, the harder ones especially offer a gratifying challenge to kids (and, let’s be frank, adults).
Fortunately, shrouding a difficult equation behind a fun and engaging riddle is the best way to get your kid interested in math well before they face the great divide in eighth grade caused by the quadratic formula. These tricky math riddles keep kids entertained while quietly sharpening their logic and math skills. Odds are, you’ll learn something, too.
Basic Math Riddles For Kids
Riddle: If there are four apples and you take away three, how many do you have?
Answer: You took three apples, so you have three!
Riddle : A grandmother, two mothers, and two daughters went to a baseball game together and bought one ticket each. How many tickets did they buy in total?
Answer : Three tickets
Explanation: The grandmother is also a mother, and the mother is also a daughter.

If eggs are 12 cents a dozen, how many eggs can you get for a dollar?
Riddle: Eggs are 12 cents a dozen. How many eggs can you get for a dollar?
Answer: 100 eggs for a penny each
Riddle: How can you add eight fours together so the total adds up to 500?
Answer: 444 + 44 + 4 + 4 + 4 = 500
Riddle: If seven people meet each other and each shake hands only once with each of the others, how many handshakes happened?
Middle School Math Riddles
Riddle: A 300 ft. train is traveling 300 ft. per minute must travel through a 300 ft. long tunnel. How long will it take the train to travel through the tunnel?
Answer: Two minutes. It takes the front of the train one minute, and the rest of the train will take two minutes to clear the tunnel.
Riddle: A cellphone and a phone case cost $110 in total. The cell phone costs $100 more than the phone case. How much was the cellphone?
Answer: $105 (not $110)

It’s not about the pizza.
Riddle: Robert and David played several golf matches against each other in a week. They played for a pizza at each match, but no pizzas were purchased until the end of the week. If Robert and David had the same number of wins at any time, those pizzas were canceled. Robert won four matches (but no pizzas), and David won three pizzas. How many rounds of golf were played?
Explanation: David won seven matches — four to cancel out Robert’s four wins and three more to win the pizzas.
Riddle: I am a three-digit number. My second digit is four times bigger than the third digit. My first digit is three less than my second digit. Who am I?
Answer: 141
Riddle: I add five to nine and get two. The answer is correct, but how?
Answer: When it is 9 a.m., add five hours to it, and you will get to 2 p.m.

Riddle: A half is a third of it. What is it?
Answer: 1 1/2
Riddle: When Miguel was 6 years old, his little sister, Leila, was half his age. If Miguel is 40 years old today, how old is Leila?
Answer: She is 37 years old.
Riddle: Tom was asked to paint numbers outside 100 apartments, which means he will have to paint numbers one through 100. How many times will he have to paint the number eight?
Answer: 20 times / Explanation: (8, 18, 28, 38, 48, 58, 68, 78, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 98)
Riddle: What can you put between a seven and an eight so that the result is greater than a seven but less than an eight?
Answer: A decimal because 7.8 is greater than seven but less than eight.

“How much is this bag of potatoes?” asked the man. “Thirty-two pounds divided by half of its own weight,” said the grocer.
Riddle: “How much is this bag of potatoes?” asked the man. “Thirty-two pounds divided by half of its own weight,” said the grocer. How much did the potatoes weigh?
Answer: 8 lbs
Riddle: When Lisa was 6 years old, her sister Lucy was half her age. If Lisa is 40 years old today, how old is Lucy?
Explanation: Lucy is three years younger than Lisa.
Riddle: You are given three positive numbers. You can add these numbers and multiply them together. The result you get will be the same. What are the numbers?
Answer: One, two, and three.
Animal Math Riddles
Riddle: There are 100 pairs of dogs in a zoo; a pair of babies are born for each dog. Unfortunately, 23 of the dogs have not survived. How many dogs are left in total?
Answer: 977 dogs
Explanation: 100 x 2 = 200; 200 + 800 = 1,000; 1,000 – 23 = 977
Riddle: If a hen and a half lay an egg and a half in a day and a half, how many eggs will half a dozen hens lay in half a dozen days?
Answer: Two dozen
Riddle: Leon works at the aquarium. When he tries to put each turtle in its own tank, he has one turtle too many. But if he puts two turtles per tank, he has one tank too many. How many turtles and how many tanks does Leon have?
Answer: He has three tanks and four turtles.

Riddle: A duck was given $9, a spider was given $36, and a bee was given $27. Based on this information, how much money would be given to a cat?
Answer: $18 ($4.50 per leg)
Riddle: If you buy a rooster to lay eggs and you expect to get three eggs each day for breakfast, how many eggs will you have after three weeks?
Answer: None. Roosters don’t lay eggs.
Riddle: A farmer has 19 sheep on his land. One day, a big storm hits, and all but seven run away. How many sheep does the farmer have left?
Answer: Seven. All but seven ran away.
Fun Math Riddles
Riddle: A group of students were standing in the blazing sun facing due west on a march past event. The leader shouted at them: Right turn! About turn! Left turn! At the end of these commands, which direction are the students facing now?
Answer: East
Explanation: They will turn 90 degrees in a right turn and then 180 degrees in an about-turn, and finally turn 90 degrees in a left turn. Therefore, the students are now facing east.

Which weighs more, 16 ounces of soda or a pound of solid gold?
Answer: Neither. They both weigh the same!
Riddle: At the time of shipping, Tom can place 10 small boxes or eight large boxes into a carton. A total of 96 boxes were sent in one shipment. The number of small boxes was less than the large boxes. What is the total number of cartons he shipped?
Answer: 11 cartons
Explanation: Four small boxes (410 = 40 boxes) + seven large boxes (78 = 56 boxes). So, 96 boxes and 11 total cartons.

Riddle: What’s the maximum number of times you can subtract five from 25?
Answer: Only once. This is because when you subtract five the first time, 25 becomes 20, then 15, and so on.
Riddle: The total cost of a pair of shoes and a hoodie is $150. The hoodie cost $100 more than the pair of shoes. How much does each item cost?
Answer: The hoodie costs $125, and the shoes cost $25.
Riddle: You have two U.S. coins with a total value of 30 cents. One of them is not a nickel. What are the two coins?
Answer: One is a quarter, and one is a nickel.
Riddle: I am a three-digit number. My tens digit is six more than my ones digit. My hundreds digit is eight less than my tens digit. What number am I?
Answer: 193
Riddle: A man is twice as old as his little sister. He is also half as old as his dad. Over a period of 50 years, his sister’s age will become half of their dad’s age. What is the age of the man now?
Answer: 50 years old
Riddle: If four men can build four tables in four hours, how many can eight men build in eight hours?
Answer : 16 tables
Riddle : There is a clothing store in Dallas. The owner has made his own method of pricing items. A vest costs $20, socks cost $25, a tie costs $15, and a blouse costs $30. Using the method, how much would a pair of underwear cost?
Answer: $45
Explanation: The pricing method consists of charging $5 for each letter required to spell the item.

Riddle: If you go to the movies and you’re paying, is it cheaper to take one friend to the movies twice or two friends to the movies at the same time?
Answer: It’s cheaper to take two friends at the same time.
Explanation: In this case, you would only be buying three tickets, whereas if you take the same friend twice, you are purchasing four tickets.
Riddle: What occurs twice a week, once a year but never in a day?
Answer: The letter E.

How many tomatoes are left in good condition?
Riddle: A little boy goes shopping and purchases 12 tomatoes. On the way home, all but nine get mushed and ruined. How many tomatoes are left in good condition?
Answer: Nine tomatoes.
Riddle: What 4 days of the week start with the letter T?
Answer: Tuesday, Thursday, Today, and Tomorrow.
Riddle: What occurs once every minute, twice in every moment, and yet never in a thousand years?
Answer: The letter M.
Riddle: How did the soccer fan know before the game that the score would be 0-0?
Answer: The score is always 0-0 before the game.
Editor’s note: All of these mind-boggling math riddles are in the public domain. However, we spotted a few of these on Kids Math Games Online , Get Riddles , Riddles.com , Everything Mom , Mash Up Math , and Greeting Card Poet , which we can’t recommend strongly enough.
This article was originally published on Feb. 26, 2021

![hard math problem solving questions [object Object]](https://www.wolframalpha.com/_next/static/images/step-by-step-need-hint_2fEuIFM8.png)
![hard math problem solving questions [object Object]](https://www.wolframalpha.com/_next/static/images/arithmetic_1O6isb1P.png)
![hard math problem solving questions [object Object]](https://www.wolframalpha.com/_next/static/images/wa-sbs-solution_2dmwSaz1.png)


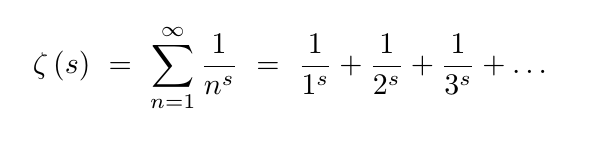


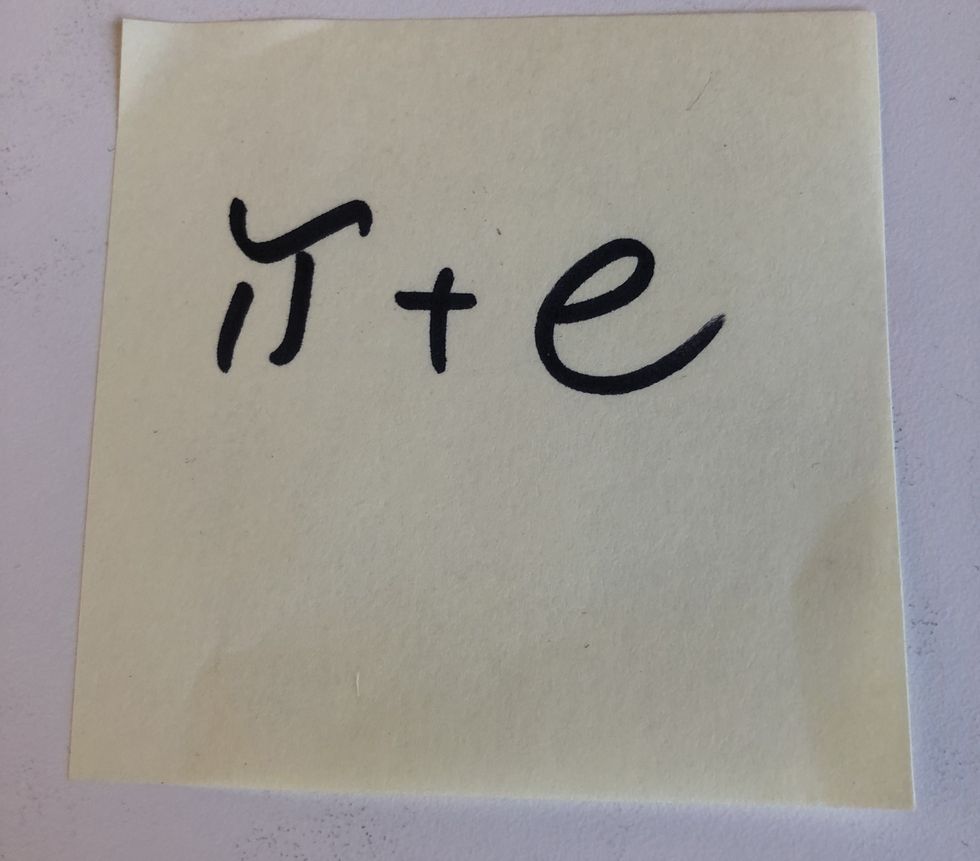
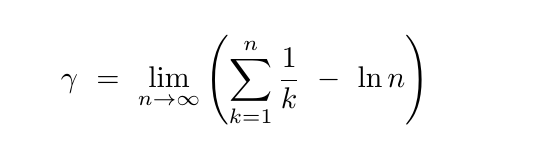
















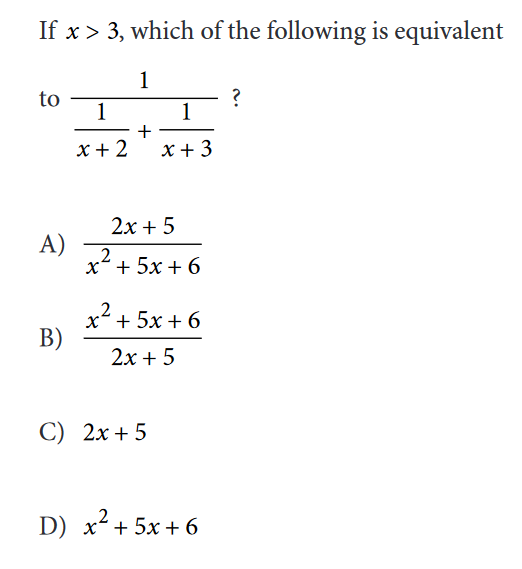


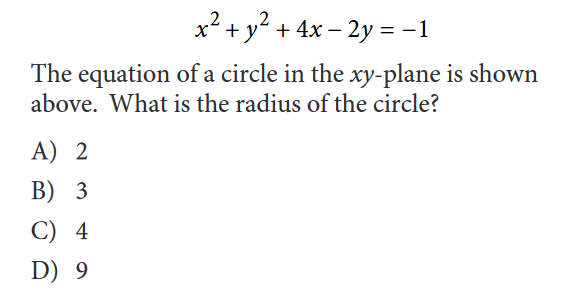


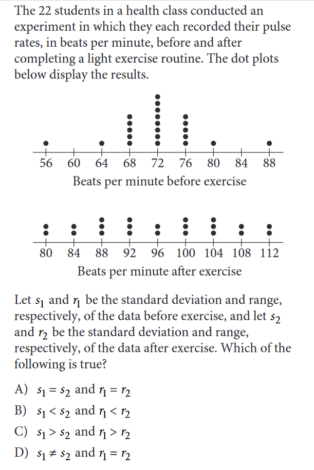
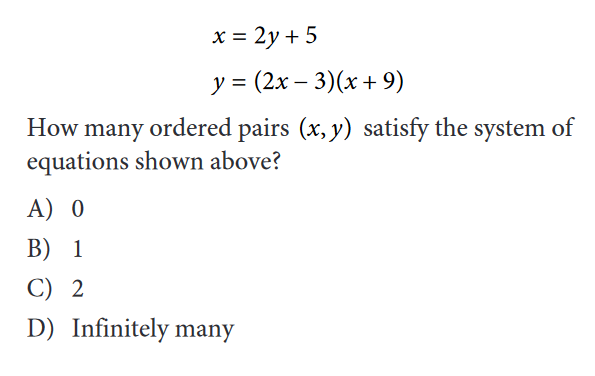


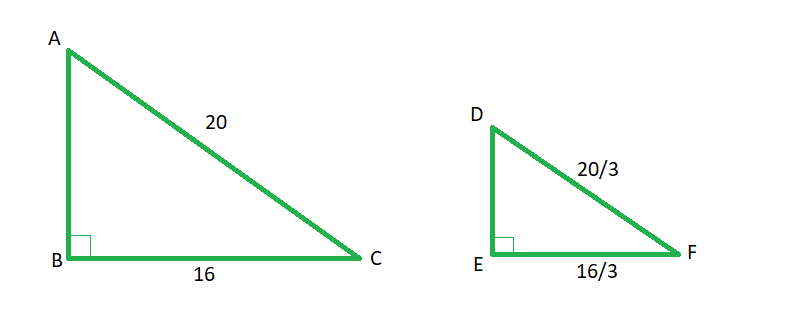
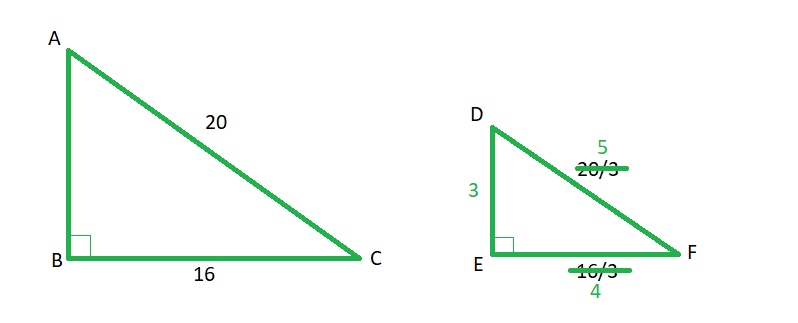


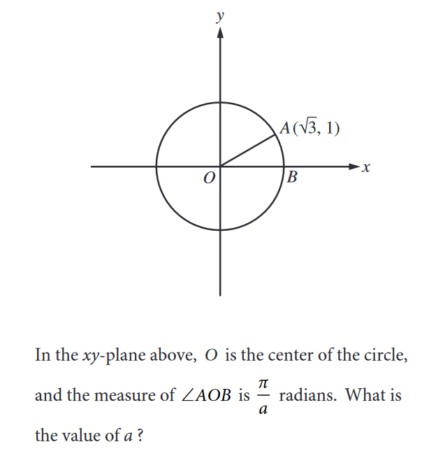
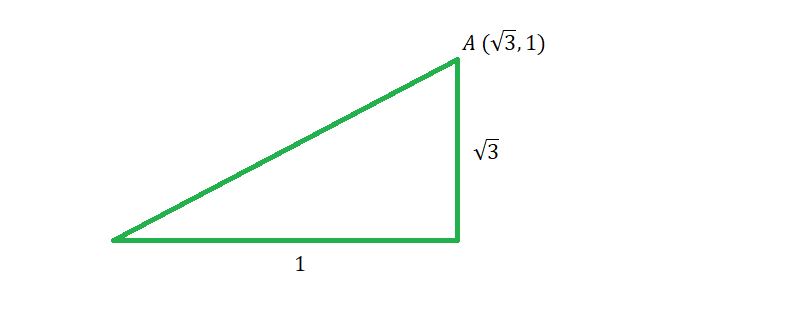








IMAGES
VIDEO
COMMENTS
Problem 6 sent by Κυριάκος There is a two-digit number whose digits are the same, and has got the following property: When squared, it produces a four-digit number, whose first two digits are the same and equal to the original's minus one, and whose last two digits are the same and equal to the half of the original's.
In 2000, the Clay Mathematics Institute, a non-profit dedicated to "increasing and disseminating mathematical knowledge," asked the world to solve seven math problems and offered $1,000,000 to ...
Answer: 1. Start by solving the division part of the equation. In order to do that, in case you forgot, you have to flip the fraction and switch from division to multiplication, thus getting 3 x 3 = 9. Now you have 9 - 9 + 1, and from there you can simply work from left to right and get your final answer: 1. 11.
Check out our top math questions that are sure to challenge and engage you. From algebra to calculus, these problems cover a range of topics and difficulty levels. ... Plainmath is a platform aimed to help users to understand how to solve math problems by providing accumulated knowledge on different topics and accessible examples.
A complete solution for the kissing problem number faces many obstacles, including computational constraints. The debate continued to solve this problem. The Bottom Line. When it comes to pushing the boundaries of the enormous human ability to comprehend and problem-solving skills, the world's hardest math problems are unquestionably the best.
They'll challenge you to look at the "problems" a different way and test your logic and problem-solving skills while you're solving. And if math isn't your strong suit, take heart—most ...
Khan Academy's 100,000+ free practice questions give instant feedback, don't need to be graded, and don't require a printer. Math Worksheets. Khan Academy. Math worksheets take forever to hunt down across the internet. Khan Academy is your one-stop-shop for practice from arithmetic to calculus. Math worksheets can vary in quality from ...
ANSWER EXPLANATION: There are two ways to solve this question. The faster way is to multiply each side of the given equation by ax−2 (so you can get rid of the fraction). When you multiply each side by ax−2, you should have: 24x2+25x−47= (−8x−3) (ax−2)−53. You should then multiply (−8x−3) and (ax−2) using FOIL.
CHALLENGING MATH PROBLEMS WORTH SOLVING DOWNLOAD OUR FAVORITE PROBLEMS FROM EVERY GRADE LEVEL Get Our Favorite Problems Take The Online Workshop WANT GOOGLE SLIDE VERSIONS OF ALL PROBLEMS? HERE'S OUR GROWING COLLECTION Get Google Slide Versions WANT TO SHARE OPEN MIDDLE WITH OTHERS? CHECK OUT THESE FREE WEBINARS TO HELP TEACHERS RETHINK CLASSWORK Elementary Version
Replace the question mark in the above diagram with an appropriate number. Answer: 6. If you enjoy playing Sudoku, then this hard math problem would have been quite a breeze for you! The rows and columns all add up to 15, and that is how the answer turned out to be 6. Solve the unfinished equation: 1 = 4. 2 = 16.
Steps. Example. Write down the inequality. ( x - 5 > 10 ) Perform the same operation on both sides. ( x - 5 + 5 > 10 + 5 ) Simplify to find the solution. ( x > 15 ) Remember, if I multiply or divide both sides of an inequality by a negative number, the direction of the inequality sign flips.
Find below a wide variety of hard word problems in algebra. Most tricky and tough algebra word problems are covered here. If you can solve these, you can probably solve any algebra problems. Teachers! Feel free to select from this list and give them to your students to see if they have mastered how to solve tough algebra problems.
The Case for Doing Hard Things . We ask hard questions because so many of the problems worth solving in life are hard. If they were easy, someone else would have solved them before you got to them. This is why college classes at top-tier universities have tests on which nearly no one clears 70%, much less gets a perfect score.
intararit. Some problems in mathematics have taken centuries to be solved, due to their complexity. Although there are some complex math problems that still elude solutions, others have now been ...
1) We don't need to solve for p and r individually. We just need to solve for (r/p). AND…. 2) The points themselves (p,r) and (2p, 5r) represent X and Y values on the line itself. (For example if p = 2 and r = 3 then that's the same thing as an x-coordinate of 2 and a y-coordinate of 3.) So let's take a look at it.
In 1988, the Australian Olympiad officials decided to throw a massive curveball to the kids on the final day of competition, and it's gone down in history as one of the toughest problems out there. Just to give you an idea of how tough it was, Australian-American mathematician Terence Tao - recipient of the 2006 Fields Medal (the mathematician ...
Math riddles and word problems combine logic and creative problem-solving. Here are 38 challenging math riddles that are perfect for kids. Menu. Riddles. 38 Hard Math Riddles (With Answers) For Future Geniuses ... shrouding a difficult equation behind a fun and engaging riddle is the best way to get your kid interested in math well before they ...
From basic additions to calculus, the process of problem solving usually takes a lot of practice before answers could come easily. As problems become more complex, it becomes even more important to understand the step-by-step process by which we solve them. At Cymath, our goal is to take your understanding of math to a new level.
Addition (Decimals) Subtraction (Decimals) Multiplication 2 (Example Problem: 3.5*8) Multiplication 3 (Example Problem: 0.3*80) Division (Decimals) Division (Decimals 2)
Only Wolfram Problem Generator directly integrates the popular and powerful Step-by-step Solutions from Wolfram|Alpha. You can use a single hint to get unstuck, or explore the entire math problem from beginning to end. Online practice problems for math, including arithmetic, algebra, calculus, linear algebra, number theory, and statistics.
One of the greatest unsolved mysteries in math is also very easy to write. Goldbach's Conjecture is, "Every even number (greater than two) is the sum of two primes.". You check this in your ...
Question 2: Calculator permitted, multiple choice. Answer: C. Category: Problem-solving and data analysis—analyzing graphical data, probability. Here's how to solve it: With problems like these, it's important that you pay attention to the wording of the question so that you know exactly what you're being asked.
Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.
A new series of reasoning models for solving hard problems. Available starting 9.12 ... They can reason through complex tasks and solve harder problems than previous models in science, coding, and math. Today, we are releasing the first of this series in ChatGPT and our API. This is a preview and we expect regular updates and improvements.
The new model, dubbed OpenAI o1, can solve problems that stump existing AI models, including OpenAI's most powerful existing model, GPT-4o. Rather than summon up an answer in one step, as a ...