null hypothesis should be rejected

What is The Null Hypothesis & When Do You Reject The Null Hypothesis

Julia Simkus

Editor at Simply Psychology

BA (Hons) Psychology, Princeton University

Julia Simkus is a graduate of Princeton University with a Bachelor of Arts in Psychology. She is currently studying for a Master's Degree in Counseling for Mental Health and Wellness in September 2023. Julia's research has been published in peer reviewed journals.

Learn about our Editorial Process

Saul McLeod, PhD

Editor-in-Chief for Simply Psychology

BSc (Hons) Psychology, MRes, PhD, University of Manchester

Saul McLeod, PhD., is a qualified psychology teacher with over 18 years of experience in further and higher education. He has been published in peer-reviewed journals, including the Journal of Clinical Psychology.

Olivia Guy-Evans, MSc

Associate Editor for Simply Psychology

BSc (Hons) Psychology, MSc Psychology of Education

Olivia Guy-Evans is a writer and associate editor for Simply Psychology. She has previously worked in healthcare and educational sectors.

On This Page:

A null hypothesis is a statistical concept suggesting no significant difference or relationship between measured variables. It’s the default assumption unless empirical evidence proves otherwise.

The null hypothesis states no relationship exists between the two variables being studied (i.e., one variable does not affect the other).

The null hypothesis is the statement that a researcher or an investigator wants to disprove.

Testing the null hypothesis can tell you whether your results are due to the effects of manipulating the dependent variable or due to random chance.

How to Write a Null Hypothesis

Null hypotheses (H0) start as research questions that the investigator rephrases as statements indicating no effect or relationship between the independent and dependent variables.

It is a default position that your research aims to challenge or confirm.

For example, if studying the impact of exercise on weight loss, your null hypothesis might be:

There is no significant difference in weight loss between individuals who exercise daily and those who do not.

Examples of Null Hypotheses

Research Question	Null Hypothesis
Do teenagers use cell phones more than adults?	Teenagers and adults use cell phones the same amount.
Do tomato plants exhibit a higher rate of growth when planted in compost rather than in soil?	Tomato plants show no difference in growth rates when planted in compost rather than soil.
Does daily meditation decrease the incidence of depression?	Daily meditation does not decrease the incidence of depression.
Does daily exercise increase test performance?	There is no relationship between daily exercise time and test performance.
Does the new vaccine prevent infections?	The vaccine does not affect the infection rate.
Does flossing your teeth affect the number of cavities?	Flossing your teeth has no effect on the number of cavities.

When Do We Reject The Null Hypothesis?

We reject the null hypothesis when the data provide strong enough evidence to conclude that it is likely incorrect. This often occurs when the p-value (probability of observing the data given the null hypothesis is true) is below a predetermined significance level.

If the collected data does not meet the expectation of the null hypothesis, a researcher can conclude that the data lacks sufficient evidence to back up the null hypothesis, and thus the null hypothesis is rejected.

Rejecting the null hypothesis means that a relationship does exist between a set of variables and the effect is statistically significant ( p > 0.05).

If the data collected from the random sample is not statistically significance , then the null hypothesis will be accepted, and the researchers can conclude that there is no relationship between the variables.

You need to perform a statistical test on your data in order to evaluate how consistent it is with the null hypothesis. A p-value is one statistical measurement used to validate a hypothesis against observed data.

Calculating the p-value is a critical part of null-hypothesis significance testing because it quantifies how strongly the sample data contradicts the null hypothesis.

The level of statistical significance is often expressed as a p -value between 0 and 1. The smaller the p-value, the stronger the evidence that you should reject the null hypothesis.

Probability and statistical significance in ab testing. Statistical significance in a b experiments

Usually, a researcher uses a confidence level of 95% or 99% (p-value of 0.05 or 0.01) as general guidelines to decide if you should reject or keep the null.

When your p-value is less than or equal to your significance level, you reject the null hypothesis.

In other words, smaller p-values are taken as stronger evidence against the null hypothesis. Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis.

In this case, the sample data provides insufficient data to conclude that the effect exists in the population.

Because you can never know with complete certainty whether there is an effect in the population, your inferences about a population will sometimes be incorrect.

When you incorrectly reject the null hypothesis, it’s called a type I error. When you incorrectly fail to reject it, it’s called a type II error.

Why Do We Never Accept The Null Hypothesis?

The reason we do not say “accept the null” is because we are always assuming the null hypothesis is true and then conducting a study to see if there is evidence against it. And, even if we don’t find evidence against it, a null hypothesis is not accepted.

A lack of evidence only means that you haven’t proven that something exists. It does not prove that something doesn’t exist.

It is risky to conclude that the null hypothesis is true merely because we did not find evidence to reject it. It is always possible that researchers elsewhere have disproved the null hypothesis, so we cannot accept it as true, but instead, we state that we failed to reject the null.

One can either reject the null hypothesis, or fail to reject it, but can never accept it.

Why Do We Use The Null Hypothesis?

We can never prove with 100% certainty that a hypothesis is true; We can only collect evidence that supports a theory. However, testing a hypothesis can set the stage for rejecting or accepting this hypothesis within a certain confidence level.

The null hypothesis is useful because it can tell us whether the results of our study are due to random chance or the manipulation of a variable (with a certain level of confidence).

A null hypothesis is rejected if the measured data is significantly unlikely to have occurred and a null hypothesis is accepted if the observed outcome is consistent with the position held by the null hypothesis.

Rejecting the null hypothesis sets the stage for further experimentation to see if a relationship between two variables exists.

Hypothesis testing is a critical part of the scientific method as it helps decide whether the results of a research study support a particular theory about a given population. Hypothesis testing is a systematic way of backing up researchers’ predictions with statistical analysis.

It helps provide sufficient statistical evidence that either favors or rejects a certain hypothesis about the population parameter.

Purpose of a Null Hypothesis

The primary purpose of the null hypothesis is to disprove an assumption.
Whether rejected or accepted, the null hypothesis can help further progress a theory in many scientific cases.
A null hypothesis can be used to ascertain how consistent the outcomes of multiple studies are.

Do you always need both a Null Hypothesis and an Alternative Hypothesis?

The null (H0) and alternative (Ha or H1) hypotheses are two competing claims that describe the effect of the independent variable on the dependent variable. They are mutually exclusive, which means that only one of the two hypotheses can be true.

While the null hypothesis states that there is no effect in the population, an alternative hypothesis states that there is statistical significance between two variables.

The goal of hypothesis testing is to make inferences about a population based on a sample. In order to undertake hypothesis testing, you must express your research hypothesis as a null and alternative hypothesis. Both hypotheses are required to cover every possible outcome of the study.

What is the difference between a null hypothesis and an alternative hypothesis?

The alternative hypothesis is the complement to the null hypothesis. The null hypothesis states that there is no effect or no relationship between variables, while the alternative hypothesis claims that there is an effect or relationship in the population.

It is the claim that you expect or hope will be true. The null hypothesis and the alternative hypothesis are always mutually exclusive, meaning that only one can be true at a time.

What are some problems with the null hypothesis?

One major problem with the null hypothesis is that researchers typically will assume that accepting the null is a failure of the experiment. However, accepting or rejecting any hypothesis is a positive result. Even if the null is not refuted, the researchers will still learn something new.

Why can a null hypothesis not be accepted?

We can either reject or fail to reject a null hypothesis, but never accept it. If your test fails to detect an effect, this is not proof that the effect doesn’t exist. It just means that your sample did not have enough evidence to conclude that it exists.

We can’t accept a null hypothesis because a lack of evidence does not prove something that does not exist. Instead, we fail to reject it.

Failing to reject the null indicates that the sample did not provide sufficient enough evidence to conclude that an effect exists.

If the p-value is greater than the significance level, then you fail to reject the null hypothesis.

Is a null hypothesis directional or non-directional?

A hypothesis test can either contain an alternative directional hypothesis or a non-directional alternative hypothesis. A directional hypothesis is one that contains the less than (“<“) or greater than (“>”) sign.

A nondirectional hypothesis contains the not equal sign (“≠”). However, a null hypothesis is neither directional nor non-directional.

A null hypothesis is a prediction that there will be no change, relationship, or difference between two variables.

The directional hypothesis or nondirectional hypothesis would then be considered alternative hypotheses to the null hypothesis.

Gill, J. (1999). The insignificance of null hypothesis significance testing. Political research quarterly , 52 (3), 647-674.

Krueger, J. (2001). Null hypothesis significance testing: On the survival of a flawed method. American Psychologist , 56 (1), 16.

Masson, M. E. (2011). A tutorial on a practical Bayesian alternative to null-hypothesis significance testing. Behavior research methods , 43 , 679-690.

Nickerson, R. S. (2000). Null hypothesis significance testing: a review of an old and continuing controversy. Psychological methods , 5 (2), 241.

Rozeboom, W. W. (1960). The fallacy of the null-hypothesis significance test. Psychological bulletin , 57 (5), 416.

Hypothesis Testing (cont...)

Hypothesis testing, the null and alternative hypothesis.

In order to undertake hypothesis testing you need to express your research hypothesis as a null and alternative hypothesis. The null hypothesis and alternative hypothesis are statements regarding the differences or effects that occur in the population. You will use your sample to test which statement (i.e., the null hypothesis or alternative hypothesis) is most likely (although technically, you test the evidence against the null hypothesis). So, with respect to our teaching example, the null and alternative hypothesis will reflect statements about all statistics students on graduate management courses.

The null hypothesis is essentially the "devil's advocate" position. That is, it assumes that whatever you are trying to prove did not happen ( hint: it usually states that something equals zero). For example, the two different teaching methods did not result in different exam performances (i.e., zero difference). Another example might be that there is no relationship between anxiety and athletic performance (i.e., the slope is zero). The alternative hypothesis states the opposite and is usually the hypothesis you are trying to prove (e.g., the two different teaching methods did result in different exam performances). Initially, you can state these hypotheses in more general terms (e.g., using terms like "effect", "relationship", etc.), as shown below for the teaching methods example:

Null Hypotheses (H ):	Undertaking seminar classes has no effect on students' performance.
Alternative Hypothesis (H ):	Undertaking seminar class has a positive effect on students' performance.

Depending on how you want to "summarize" the exam performances will determine how you might want to write a more specific null and alternative hypothesis. For example, you could compare the mean exam performance of each group (i.e., the "seminar" group and the "lectures-only" group). This is what we will demonstrate here, but other options include comparing the distributions , medians , amongst other things. As such, we can state:

Null Hypotheses (H ):	The mean exam mark for the "seminar" and "lecture-only" teaching methods is the same in the population.
Alternative Hypothesis (H ):	The mean exam mark for the "seminar" and "lecture-only" teaching methods is not the same in the population.

Now that you have identified the null and alternative hypotheses, you need to find evidence and develop a strategy for declaring your "support" for either the null or alternative hypothesis. We can do this using some statistical theory and some arbitrary cut-off points. Both these issues are dealt with next.

Significance levels

The level of statistical significance is often expressed as the so-called p -value . Depending on the statistical test you have chosen, you will calculate a probability (i.e., the p -value) of observing your sample results (or more extreme) given that the null hypothesis is true . Another way of phrasing this is to consider the probability that a difference in a mean score (or other statistic) could have arisen based on the assumption that there really is no difference. Let us consider this statement with respect to our example where we are interested in the difference in mean exam performance between two different teaching methods. If there really is no difference between the two teaching methods in the population (i.e., given that the null hypothesis is true), how likely would it be to see a difference in the mean exam performance between the two teaching methods as large as (or larger than) that which has been observed in your sample?

So, you might get a p -value such as 0.03 (i.e., p = .03). This means that there is a 3% chance of finding a difference as large as (or larger than) the one in your study given that the null hypothesis is true. However, you want to know whether this is "statistically significant". Typically, if there was a 5% or less chance (5 times in 100 or less) that the difference in the mean exam performance between the two teaching methods (or whatever statistic you are using) is as different as observed given the null hypothesis is true, you would reject the null hypothesis and accept the alternative hypothesis. Alternately, if the chance was greater than 5% (5 times in 100 or more), you would fail to reject the null hypothesis and would not accept the alternative hypothesis. As such, in this example where p = .03, we would reject the null hypothesis and accept the alternative hypothesis. We reject it because at a significance level of 0.03 (i.e., less than a 5% chance), the result we obtained could happen too frequently for us to be confident that it was the two teaching methods that had an effect on exam performance.

Whilst there is relatively little justification why a significance level of 0.05 is used rather than 0.01 or 0.10, for example, it is widely used in academic research. However, if you want to be particularly confident in your results, you can set a more stringent level of 0.01 (a 1% chance or less; 1 in 100 chance or less).

One- and two-tailed predictions

When considering whether we reject the null hypothesis and accept the alternative hypothesis, we need to consider the direction of the alternative hypothesis statement. For example, the alternative hypothesis that was stated earlier is:

Alternative Hypothesis (H ):

Undertaking seminar classes has a positive effect on students' performance.

The alternative hypothesis tells us two things. First, what predictions did we make about the effect of the independent variable(s) on the dependent variable(s)? Second, what was the predicted direction of this effect? Let's use our example to highlight these two points.

Sarah predicted that her teaching method (independent variable: teaching method), whereby she not only required her students to attend lectures, but also seminars, would have a positive effect (that is, increased) students' performance (dependent variable: exam marks). If an alternative hypothesis has a direction (and this is how you want to test it), the hypothesis is one-tailed. That is, it predicts direction of the effect. If the alternative hypothesis has stated that the effect was expected to be negative, this is also a one-tailed hypothesis.

Alternatively, a two-tailed prediction means that we do not make a choice over the direction that the effect of the experiment takes. Rather, it simply implies that the effect could be negative or positive. If Sarah had made a two-tailed prediction, the alternative hypothesis might have been:

Alternative Hypothesis (H ):

Undertaking seminar classes has an effect on students' performance.

In other words, we simply take out the word "positive", which implies the direction of our effect. In our example, making a two-tailed prediction may seem strange. After all, it would be logical to expect that "extra" tuition (going to seminar classes as well as lectures) would either have a positive effect on students' performance or no effect at all, but certainly not a negative effect. However, this is just our opinion (and hope) and certainly does not mean that we will get the effect we expect. Generally speaking, making a one-tail prediction (i.e., and testing for it this way) is frowned upon as it usually reflects the hope of a researcher rather than any certainty that it will happen. Notable exceptions to this rule are when there is only one possible way in which a change could occur. This can happen, for example, when biological activity/presence in measured. That is, a protein might be "dormant" and the stimulus you are using can only possibly "wake it up" (i.e., it cannot possibly reduce the activity of a "dormant" protein). In addition, for some statistical tests, one-tailed tests are not possible.

Rejecting or failing to reject the null hypothesis

Let's return finally to the question of whether we reject or fail to reject the null hypothesis.

If our statistical analysis shows that the significance level is below the cut-off value we have set (e.g., either 0.05 or 0.01), we reject the null hypothesis and accept the alternative hypothesis. Alternatively, if the significance level is above the cut-off value, we fail to reject the null hypothesis and cannot accept the alternative hypothesis. You should note that you cannot accept the null hypothesis, but only find evidence against it.

Support or Reject Null Hypothesis in Easy Steps

What does it mean to reject the null hypothesis.

General Situations: P Value
P Value Guidelines
A Proportion
A Proportion (second example)

In many statistical tests, you’ll want to either reject or support the null hypothesis . For elementary statistics students, the term can be a tricky term to grasp, partly because the name “null hypothesis” doesn’t make it clear about what the null hypothesis actually is!

The null hypothesis can be thought of as a nullifiable hypothesis. That means you can nullify it, or reject it. What happens if you reject the null hypothesis? It gets replaced with the alternate hypothesis, which is what you think might actually be true about a situation. For example, let’s say you think that a certain drug might be responsible for a spate of recent heart attacks. The drug company thinks the drug is safe. The null hypothesis is always the accepted hypothesis; in this example, the drug is on the market, people are using it, and it’s generally accepted to be safe. Therefore, the null hypothesis is that the drug is safe. The alternate hypothesis — the one you want to replace the null hypothesis, is that the drug isn’t safe. Rejecting the null hypothesis in this case means that you will have to prove that the drug is not safe.

To reject the null hypothesis, perform the following steps:

Step 1: State the null hypothesis. When you state the null hypothesis, you also have to state the alternate hypothesis. Sometimes it is easier to state the alternate hypothesis first, because that’s the researcher’s thoughts about the experiment. How to state the null hypothesis (opens in a new window).

Step 2: Support or reject the null hypothesis . Several methods exist, depending on what kind of sample data you have. For example, you can use the P-value method. For a rundown on all methods, see: Support or reject the null hypothesis.

If you are able to reject the null hypothesis in Step 2, you can replace it with the alternate hypothesis.

That’s it!

When to Reject the Null hypothesis

Basically, you reject the null hypothesis when your test value falls into the rejection region . There are four main ways you’ll compute test values and either support or reject your null hypothesis. Which method you choose depends mainly on if you have a proportion or a p-value .

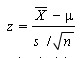
Support or Reject the Null Hypothesis: Steps

Click the link the skip to the situation you need to support or reject null hypothesis for: General Situations: P Value P Value Guidelines A Proportion A Proportion (second example)

Support or Reject Null Hypothesis with a P Value

If you have a P-value , or are asked to find a p-value, follow these instructions to support or reject the null hypothesis. This method works if you are given an alpha level and if you are not given an alpha level. If you are given a confidence level , just subtract from 1 to get the alpha level. See: How to calculate an alpha level .

Step 1: State the null hypothesis and the alternate hypothesis (“the claim”). If you aren’t sure how to do this, follow this link for How To State the Null and Alternate Hypothesis .

Step 2: Find the critical value . We’re dealing with a normally distributed population, so the critical value is a z-score . Use the following formula to find the z-score .

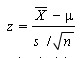
Click here if you want easy, step-by-step instructions for solving this formula.

Step 4: Find the P-Value by looking up your answer from step 3 in the z-table . To get the p-value, subtract the area from 1. For example, if your area is .990 then your p-value is 1-.9950 = 0.005. Note: for a two-tailed test , you’ll need to halve this amount to get the p-value in one tail.

Step 5: Compare your answer from step 4 with the α value given in the question. Should you support or reject the null hypothesis? If step 7 is less than or equal to α, reject the null hypothesis, otherwise do not reject it.

P-Value Guidelines

Use these general guidelines to decide if you should reject or keep the null:

If p value > .10 → “not significant ” If p value ≤ .10 → “marginally significant” If p value ≤ .05 → “significant” If p value ≤ .01 → “highly significant.”

Support or Reject Null Hypothesis for a Proportion

Sometimes, you’ll be given a proportion of the population or a percentage and asked to support or reject null hypothesis. In this case you can’t compute a test value by calculating a z-score (you need actual numbers for that), so we use a slightly different technique.

Example question: A researcher claims that Democrats will win the next election. 4300 voters were polled; 2200 said they would vote Democrat. Decide if you should support or reject null hypothesis. Is there enough evidence at α=0.05 to support this claim?

Step 1: State the null hypothesis and the alternate hypothesis (“the claim”) . H o :p ≤ 0.5 H 1 :p > .5

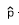
Step 3: Use the following formula to calculate your test value.

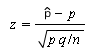
Where: Phat is calculated in Step 2 P the null hypothesis p value (.05) Q is 1 – p

The z-score is: .512 – .5 / √(.5(.5) / 4300)) = 1.57

Step 4: Look up Step 3 in the z-table to get .9418.

Step 5: Calculate your p-value by subtracting Step 4 from 1. 1-.9418 = .0582

Step 6: Compare your answer from step 5 with the α value given in the question . Support or reject the null hypothesis? If step 5 is less than α, reject the null hypothesis, otherwise do not reject it. In this case, .582 (5.82%) is not less than our α, so we do not reject the null hypothesis.

Support or Reject Null Hypothesis for a Proportion: Second example

Example question: A researcher claims that more than 23% of community members go to church regularly. In a recent survey, 126 out of 420 people stated they went to church regularly. Is there enough evidence at α = 0.05 to support this claim? Use the P-Value method to support or reject null hypothesis.

Step 1: State the null hypothesis and the alternate hypothesis (“the claim”) . H o :p ≤ 0.23; H 1 :p > 0.23 (claim)

Step 3: Find ‘p’ by converting the stated claim to a decimal: 23% = 0.23. Also, find ‘q’ by subtracting ‘p’ from 1: 1 – 0.23 = 0.77.

Step 4: Use the following formula to calculate your test value.

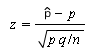
If formulas confuse you, this is asking you to:

Multiply p and q together, then divide by the number in the random sample. (0.23 x 0.77) / 420 = 0.00042
Take the square root of your answer to 2 . √( 0.1771) = 0. 0205
Divide your answer to 1. by your answer in 3. 0.07 / 0. 0205 = 3.41

Step 5: Find the P-Value by looking up your answer from step 5 in the z-table . The z-score for 3.41 is .4997. Subtract from 0.500: 0.500-.4997 = 0.003.

Step 6: Compare your P-value to α . Support or reject null hypothesis? If the P-value is less, reject the null hypothesis. If the P-value is more, keep the null hypothesis. 0.003 < 0.05, so we have enough evidence to reject the null hypothesis and accept the claim.

Note: In Step 5, I’m using the z-table on this site to solve this problem. Most textbooks have the right of z-table . If you’re seeing .9997 as an answer in your textbook table, then your textbook has a “whole z” table, in which case don’t subtract from .5, subtract from 1. 1-.9997 = 0.003.

Check out our Youtube channel for video tips!

Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics , Cambridge University Press. Gonick, L. (1993). The Cartoon Guide to Statistics . HarperPerennial.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 13: Inferential Statistics

Understanding Null Hypothesis Testing

Learning Objectives

Explain the purpose of null hypothesis testing, including the role of sampling error.
Describe the basic logic of null hypothesis testing.
Describe the role of relationship strength and sample size in determining statistical significance and make reasonable judgments about statistical significance based on these two factors.

The Purpose of Null Hypothesis Testing

As we have seen, psychological research typically involves measuring one or more variables for a sample and computing descriptive statistics for that sample. In general, however, the researcher’s goal is not to draw conclusions about that sample but to draw conclusions about the population that the sample was selected from. Thus researchers must use sample statistics to draw conclusions about the corresponding values in the population. These corresponding values in the population are called parameters . Imagine, for example, that a researcher measures the number of depressive symptoms exhibited by each of 50 clinically depressed adults and computes the mean number of symptoms. The researcher probably wants to use this sample statistic (the mean number of symptoms for the sample) to draw conclusions about the corresponding population parameter (the mean number of symptoms for clinically depressed adults).

Unfortunately, sample statistics are not perfect estimates of their corresponding population parameters. This is because there is a certain amount of random variability in any statistic from sample to sample. The mean number of depressive symptoms might be 8.73 in one sample of clinically depressed adults, 6.45 in a second sample, and 9.44 in a third—even though these samples are selected randomly from the same population. Similarly, the correlation (Pearson’s r ) between two variables might be +.24 in one sample, −.04 in a second sample, and +.15 in a third—again, even though these samples are selected randomly from the same population. This random variability in a statistic from sample to sample is called sampling error . (Note that the term error here refers to random variability and does not imply that anyone has made a mistake. No one “commits a sampling error.”)

One implication of this is that when there is a statistical relationship in a sample, it is not always clear that there is a statistical relationship in the population. A small difference between two group means in a sample might indicate that there is a small difference between the two group means in the population. But it could also be that there is no difference between the means in the population and that the difference in the sample is just a matter of sampling error. Similarly, a Pearson’s r value of −.29 in a sample might mean that there is a negative relationship in the population. But it could also be that there is no relationship in the population and that the relationship in the sample is just a matter of sampling error.

In fact, any statistical relationship in a sample can be interpreted in two ways:

There is a relationship in the population, and the relationship in the sample reflects this.
There is no relationship in the population, and the relationship in the sample reflects only sampling error.

The purpose of null hypothesis testing is simply to help researchers decide between these two interpretations.

The Logic of Null Hypothesis Testing

Null hypothesis testing is a formal approach to deciding between two interpretations of a statistical relationship in a sample. One interpretation is called the null hypothesis (often symbolized H 0 and read as “H-naught”). This is the idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error. Informally, the null hypothesis is that the sample relationship “occurred by chance.” The other interpretation is called the alternative hypothesis (often symbolized as H 1 ). This is the idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.

Again, every statistical relationship in a sample can be interpreted in either of these two ways: It might have occurred by chance, or it might reflect a relationship in the population. So researchers need a way to decide between them. Although there are many specific null hypothesis testing techniques, they are all based on the same general logic. The steps are as follows:

Assume for the moment that the null hypothesis is true. There is no relationship between the variables in the population.
Determine how likely the sample relationship would be if the null hypothesis were true.
If the sample relationship would be extremely unlikely, then reject the null hypothesis in favour of the alternative hypothesis. If it would not be extremely unlikely, then retain the null hypothesis .

Following this logic, we can begin to understand why Mehl and his colleagues concluded that there is no difference in talkativeness between women and men in the population. In essence, they asked the following question: “If there were no difference in the population, how likely is it that we would find a small difference of d = 0.06 in our sample?” Their answer to this question was that this sample relationship would be fairly likely if the null hypothesis were true. Therefore, they retained the null hypothesis—concluding that there is no evidence of a sex difference in the population. We can also see why Kanner and his colleagues concluded that there is a correlation between hassles and symptoms in the population. They asked, “If the null hypothesis were true, how likely is it that we would find a strong correlation of +.60 in our sample?” Their answer to this question was that this sample relationship would be fairly unlikely if the null hypothesis were true. Therefore, they rejected the null hypothesis in favour of the alternative hypothesis—concluding that there is a positive correlation between these variables in the population.

A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value . A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A high p value means that the sample result would be likely if the null hypothesis were true and leads to the retention of the null hypothesis. But how low must the p value be before the sample result is considered unlikely enough to reject the null hypothesis? In null hypothesis testing, this criterion is called α (alpha) and is almost always set to .05. If there is less than a 5% chance of a result as extreme as the sample result if the null hypothesis were true, then the null hypothesis is rejected. When this happens, the result is said to be statistically significant . If there is greater than a 5% chance of a result as extreme as the sample result when the null hypothesis is true, then the null hypothesis is retained. This does not necessarily mean that the researcher accepts the null hypothesis as true—only that there is not currently enough evidence to conclude that it is true. Researchers often use the expression “fail to reject the null hypothesis” rather than “retain the null hypothesis,” but they never use the expression “accept the null hypothesis.”

The Misunderstood p Value

The p value is one of the most misunderstood quantities in psychological research (Cohen, 1994) [1] . Even professional researchers misinterpret it, and it is not unusual for such misinterpretations to appear in statistics textbooks!

The most common misinterpretation is that the p value is the probability that the null hypothesis is true—that the sample result occurred by chance. For example, a misguided researcher might say that because the p value is .02, there is only a 2% chance that the result is due to chance and a 98% chance that it reflects a real relationship in the population. But this is incorrect . The p value is really the probability of a result at least as extreme as the sample result if the null hypothesis were true. So a p value of .02 means that if the null hypothesis were true, a sample result this extreme would occur only 2% of the time.

You can avoid this misunderstanding by remembering that the p value is not the probability that any particular hypothesis is true or false. Instead, it is the probability of obtaining the sample result if the null hypothesis were true.

Role of Sample Size and Relationship Strength

Recall that null hypothesis testing involves answering the question, “If the null hypothesis were true, what is the probability of a sample result as extreme as this one?” In other words, “What is the p value?” It can be helpful to see that the answer to this question depends on just two considerations: the strength of the relationship and the size of the sample. Specifically, the stronger the sample relationship and the larger the sample, the less likely the result would be if the null hypothesis were true. That is, the lower the p value. This should make sense. Imagine a study in which a sample of 500 women is compared with a sample of 500 men in terms of some psychological characteristic, and Cohen’s d is a strong 0.50. If there were really no sex difference in the population, then a result this strong based on such a large sample should seem highly unlikely. Now imagine a similar study in which a sample of three women is compared with a sample of three men, and Cohen’s d is a weak 0.10. If there were no sex difference in the population, then a relationship this weak based on such a small sample should seem likely. And this is precisely why the null hypothesis would be rejected in the first example and retained in the second.

Of course, sometimes the result can be weak and the sample large, or the result can be strong and the sample small. In these cases, the two considerations trade off against each other so that a weak result can be statistically significant if the sample is large enough and a strong relationship can be statistically significant even if the sample is small. Table 13.1 shows roughly how relationship strength and sample size combine to determine whether a sample result is statistically significant. The columns of the table represent the three levels of relationship strength: weak, medium, and strong. The rows represent four sample sizes that can be considered small, medium, large, and extra large in the context of psychological research. Thus each cell in the table represents a combination of relationship strength and sample size. If a cell contains the word Yes , then this combination would be statistically significant for both Cohen’s d and Pearson’s r . If it contains the word No , then it would not be statistically significant for either. There is one cell where the decision for d and r would be different and another where it might be different depending on some additional considerations, which are discussed in Section 13.2 “Some Basic Null Hypothesis Tests”

Table 13.1 How Relationship Strength and Sample Size Combine to Determine Whether a Result Is Statistically Significant
Sample Size	Weak relationship	Medium-strength relationship	Strong relationship
Small ( = 20)	No	No	= Maybe = Yes
Medium ( = 50)	No	Yes	Yes
Large ( = 100)	= Yes = No	Yes	Yes
Extra large ( = 500)	Yes	Yes	Yes

Although Table 13.1 provides only a rough guideline, it shows very clearly that weak relationships based on medium or small samples are never statistically significant and that strong relationships based on medium or larger samples are always statistically significant. If you keep this lesson in mind, you will often know whether a result is statistically significant based on the descriptive statistics alone. It is extremely useful to be able to develop this kind of intuitive judgment. One reason is that it allows you to develop expectations about how your formal null hypothesis tests are going to come out, which in turn allows you to detect problems in your analyses. For example, if your sample relationship is strong and your sample is medium, then you would expect to reject the null hypothesis. If for some reason your formal null hypothesis test indicates otherwise, then you need to double-check your computations and interpretations. A second reason is that the ability to make this kind of intuitive judgment is an indication that you understand the basic logic of this approach in addition to being able to do the computations.

Statistical Significance Versus Practical Significance

Table 13.1 illustrates another extremely important point. A statistically significant result is not necessarily a strong one. Even a very weak result can be statistically significant if it is based on a large enough sample. This is closely related to Janet Shibley Hyde’s argument about sex differences (Hyde, 2007) [2] . The differences between women and men in mathematical problem solving and leadership ability are statistically significant. But the word significant can cause people to interpret these differences as strong and important—perhaps even important enough to influence the college courses they take or even who they vote for. As we have seen, however, these statistically significant differences are actually quite weak—perhaps even “trivial.”

This is why it is important to distinguish between the statistical significance of a result and the practical significance of that result. Practical significance refers to the importance or usefulness of the result in some real-world context. Many sex differences are statistically significant—and may even be interesting for purely scientific reasons—but they are not practically significant. In clinical practice, this same concept is often referred to as “clinical significance.” For example, a study on a new treatment for social phobia might show that it produces a statistically significant positive effect. Yet this effect still might not be strong enough to justify the time, effort, and other costs of putting it into practice—especially if easier and cheaper treatments that work almost as well already exist. Although statistically significant, this result would be said to lack practical or clinical significance.

Key Takeaways

Null hypothesis testing is a formal approach to deciding whether a statistical relationship in a sample reflects a real relationship in the population or is just due to chance.
The logic of null hypothesis testing involves assuming that the null hypothesis is true, finding how likely the sample result would be if this assumption were correct, and then making a decision. If the sample result would be unlikely if the null hypothesis were true, then it is rejected in favour of the alternative hypothesis. If it would not be unlikely, then the null hypothesis is retained.
The probability of obtaining the sample result if the null hypothesis were true (the p value) is based on two considerations: relationship strength and sample size. Reasonable judgments about whether a sample relationship is statistically significant can often be made by quickly considering these two factors.
Statistical significance is not the same as relationship strength or importance. Even weak relationships can be statistically significant if the sample size is large enough. It is important to consider relationship strength and the practical significance of a result in addition to its statistical significance.
Discussion: Imagine a study showing that people who eat more broccoli tend to be happier. Explain for someone who knows nothing about statistics why the researchers would conduct a null hypothesis test.
The correlation between two variables is r = −.78 based on a sample size of 137.
The mean score on a psychological characteristic for women is 25 ( SD = 5) and the mean score for men is 24 ( SD = 5). There were 12 women and 10 men in this study.
In a memory experiment, the mean number of items recalled by the 40 participants in Condition A was 0.50 standard deviations greater than the mean number recalled by the 40 participants in Condition B.
In another memory experiment, the mean scores for participants in Condition A and Condition B came out exactly the same!
A student finds a correlation of r = .04 between the number of units the students in his research methods class are taking and the students’ level of stress.

Long Descriptions

“Null Hypothesis” long description: A comic depicting a man and a woman talking in the foreground. In the background is a child working at a desk. The man says to the woman, “I can’t believe schools are still teaching kids about the null hypothesis. I remember reading a big study that conclusively disproved it years ago.” [Return to “Null Hypothesis”]

“Conditional Risk” long description: A comic depicting two hikers beside a tree during a thunderstorm. A bolt of lightning goes “crack” in the dark sky as thunder booms. One of the hikers says, “Whoa! We should get inside!” The other hiker says, “It’s okay! Lightning only kills about 45 Americans a year, so the chances of dying are only one in 7,000,000. Let’s go on!” The comic’s caption says, “The annual death rate among people who know that statistic is one in six.” [Return to “Conditional Risk”]

Media Attributions

Null Hypothesis by XKCD CC BY-NC (Attribution NonCommercial)
Conditional Risk by XKCD CC BY-NC (Attribution NonCommercial)
Cohen, J. (1994). The world is round: p < .05. American Psychologist, 49 , 997–1003. ↵
Hyde, J. S. (2007). New directions in the study of gender similarities and differences. Current Directions in Psychological Science, 16 , 259–263. ↵

Values in a population that correspond to variables measured in a study.

The random variability in a statistic from sample to sample.

A formal approach to deciding between two interpretations of a statistical relationship in a sample.

The idea that there is no relationship in the population and that the relationship in the sample reflects only sampling error.

The idea that there is a relationship in the population and that the relationship in the sample reflects this relationship in the population.

When the relationship found in the sample would be extremely unlikely, the idea that the relationship occurred “by chance” is rejected.

When the relationship found in the sample is likely to have occurred by chance, the null hypothesis is not rejected.

The probability that, if the null hypothesis were true, the result found in the sample would occur.

How low the p value must be before the sample result is considered unlikely in null hypothesis testing.

When there is less than a 5% chance of a result as extreme as the sample result occurring and the null hypothesis is rejected.

Research Methods in Psychology - 2nd Canadian Edition Copyright © 2015 by Paul C. Price, Rajiv Jhangiani, & I-Chant A. Chiang is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

Have a language expert improve your writing

Run a free plagiarism check in 10 minutes, generate accurate citations for free.

Knowledge Base
Null and Alternative Hypotheses | Definitions & Examples

Null & Alternative Hypotheses | Definitions, Templates & Examples

Published on May 6, 2022 by Shaun Turney . Revised on June 22, 2023.

The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :

Null hypothesis ( H 0 ): There’s no effect in the population .
Alternative hypothesis ( H a or H 1 ) : There’s an effect in the population.

Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, similarities and differences between null and alternative hypotheses, how to write null and alternative hypotheses, other interesting articles, frequently asked questions.

The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”:

The null hypothesis ( H 0 ) answers “No, there’s no effect in the population.”
The alternative hypothesis ( H a ) answers “Yes, there is an effect in the population.”

The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample. It’s critical for your research to write strong hypotheses .

You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.

Receive feedback on language, structure, and formatting

Professional editors proofread and edit your paper by focusing on:

Academic style
Vague sentences
Style consistency

See an example

The null hypothesis is the claim that there’s no effect in the population.

If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.

Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept . Be careful not to say you “prove” or “accept” the null hypothesis.

Null hypotheses often include phrases such as “no effect,” “no difference,” or “no relationship.” When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).

You can never know with complete certainty whether there is an effect in the population. Some percentage of the time, your inference about the population will be incorrect. When you incorrectly reject the null hypothesis, it’s called a type I error . When you incorrectly fail to reject it, it’s a type II error.

Examples of null hypotheses

The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.

	( )

Does tooth flossing affect the number of cavities?	Tooth flossing has on the number of cavities.	test: The mean number of cavities per person does not differ between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ = µ .
Does the amount of text highlighted in the textbook affect exam scores?	The amount of text highlighted in the textbook has on exam scores.	: There is no relationship between the amount of text highlighted and exam scores in the population; β = 0.
Does daily meditation decrease the incidence of depression?	Daily meditation the incidence of depression.*	test: The proportion of people with depression in the daily-meditation group ( ) is greater than or equal to the no-meditation group ( ) in the population; ≥ .

*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .

The alternative hypothesis ( H a ) is the other answer to your research question . It claims that there’s an effect in the population.

Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.

The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.

Alternative hypotheses often include phrases such as “an effect,” “a difference,” or “a relationship.” When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes < or >). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.

Examples of alternative hypotheses

The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.



Does tooth flossing affect the number of cavities?	Tooth flossing has an on the number of cavities.	test: The mean number of cavities per person differs between the flossing group (µ ) and the non-flossing group (µ ) in the population; µ ≠ µ .
Does the amount of text highlighted in a textbook affect exam scores?	The amount of text highlighted in the textbook has an on exam scores.	: There is a relationship between the amount of text highlighted and exam scores in the population; β ≠ 0.
Does daily meditation decrease the incidence of depression?	Daily meditation the incidence of depression.	test: The proportion of people with depression in the daily-meditation group ( ) is less than the no-meditation group ( ) in the population; < .

Null and alternative hypotheses are similar in some ways:

They’re both answers to the research question.
They both make claims about the population.
They’re both evaluated by statistical tests.

However, there are important differences between the two types of hypotheses, summarized in the following table.


	A claim that there is in the population.	A claim that there is in the population.


	Equality symbol (=, ≥, or ≤)	Inequality symbol (≠, <, or >)
	Rejected	Supported
	Failed to reject	Not supported

Prevent plagiarism. Run a free check.

To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.

General template sentences

The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:

Does independent variable affect dependent variable ?

Null hypothesis ( H 0 ): Independent variable does not affect dependent variable.
Alternative hypothesis ( H a ): Independent variable affects dependent variable.

Test-specific template sentences

Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.

	( )
test with two groups	The mean dependent variable does not differ between group 1 (µ ) and group 2 (µ ) in the population; µ = µ .	The mean dependent variable differs between group 1 (µ ) and group 2 (µ ) in the population; µ ≠ µ .
with three groups	The mean dependent variable does not differ between group 1 (µ ), group 2 (µ ), and group 3 (µ ) in the population; µ = µ = µ .	The mean dependent variable of group 1 (µ ), group 2 (µ ), and group 3 (µ ) are not all equal in the population.
	There is no correlation between independent variable and dependent variable in the population; ρ = 0.	There is a correlation between independent variable and dependent variable in the population; ρ ≠ 0.
	There is no relationship between independent variable and dependent variable in the population; β = 0.	There is a relationship between independent variable and dependent variable in the population; β ≠ 0.
Two-proportions test	The dependent variable expressed as a proportion does not differ between group 1 ( ) and group 2 ( ) in the population; = .	The dependent variable expressed as a proportion differs between group 1 ( ) and group 2 ( ) in the population; ≠ .

Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.

If you want to know more about statistics , methodology , or research bias , make sure to check out some of our other articles with explanations and examples.

Normal distribution
Descriptive statistics
Measures of central tendency
Correlation coefficient

Methodology

Cluster sampling
Stratified sampling
Types of interviews
Cohort study
Thematic analysis

Research bias

Implicit bias
Cognitive bias
Survivorship bias
Availability heuristic
Nonresponse bias
Regression to the mean

Hypothesis testing is a formal procedure for investigating our ideas about the world using statistics. It is used by scientists to test specific predictions, called hypotheses , by calculating how likely it is that a pattern or relationship between variables could have arisen by chance.

Null and alternative hypotheses are used in statistical hypothesis testing . The null hypothesis of a test always predicts no effect or no relationship between variables, while the alternative hypothesis states your research prediction of an effect or relationship.

The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).

The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (“ x affects y because …”).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses . In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the “Cite this Scribbr article” button to automatically add the citation to our free Citation Generator.

Turney, S. (2023, June 22). Null & Alternative Hypotheses | Definitions, Templates & Examples. Scribbr. Retrieved September 27, 2024, from https://www.scribbr.com/statistics/null-and-alternative-hypotheses/

Is this article helpful?

Shaun Turney

Other students also liked, inferential statistics | an easy introduction & examples, hypothesis testing | a step-by-step guide with easy examples, type i & type ii errors | differences, examples, visualizations, what is your plagiarism score.

13.1 Understanding Null Hypothesis Testing

Learning objectives.

Explain the purpose of null hypothesis testing, including the role of sampling error.
Describe the basic logic of null hypothesis testing.
Describe the role of relationship strength and sample size in determining statistical significance and make reasonable judgments about statistical significance based on these two factors.

The Purpose of Null Hypothesis Testing

As we have seen, psychological research typically involves measuring one or more variables in a sample and computing descriptive statistics for that sample. In general, however, the researcher’s goal is not to draw conclusions about that sample but to draw conclusions about the population that the sample was selected from. Thus researchers must use sample statistics to draw conclusions about the corresponding values in the population. These corresponding values in the population are called parameters . Imagine, for example, that a researcher measures the number of depressive symptoms exhibited by each of 50 adults with clinical depression and computes the mean number of symptoms. The researcher probably wants to use this sample statistic (the mean number of symptoms for the sample) to draw conclusions about the corresponding population parameter (the mean number of symptoms for adults with clinical depression).

Unfortunately, sample statistics are not perfect estimates of their corresponding population parameters. This is because there is a certain amount of random variability in any statistic from sample to sample. The mean number of depressive symptoms might be 8.73 in one sample of adults with clinical depression, 6.45 in a second sample, and 9.44 in a third—even though these samples are selected randomly from the same population. Similarly, the correlation (Pearson’s r ) between two variables might be +.24 in one sample, −.04 in a second sample, and +.15 in a third—again, even though these samples are selected randomly from the same population. This random variability in a statistic from sample to sample is called sampling error . (Note that the term error here refers to random variability and does not imply that anyone has made a mistake. No one “commits a sampling error.”)

In fact, any statistical relationship in a sample can be interpreted in two ways:

There is a relationship in the population, and the relationship in the sample reflects this.
There is no relationship in the population, and the relationship in the sample reflects only sampling error.

The purpose of null hypothesis testing is simply to help researchers decide between these two interpretations.

The Logic of Null Hypothesis Testing

Assume for the moment that the null hypothesis is true. There is no relationship between the variables in the population.
Determine how likely the sample relationship would be if the null hypothesis were true.
If the sample relationship would be extremely unlikely, then reject the null hypothesis in favor of the alternative hypothesis. If it would not be extremely unlikely, then retain the null hypothesis .

Following this logic, we can begin to understand why Mehl and his colleagues concluded that there is no difference in talkativeness between women and men in the population. In essence, they asked the following question: “If there were no difference in the population, how likely is it that we would find a small difference of d = 0.06 in our sample?” Their answer to this question was that this sample relationship would be fairly likely if the null hypothesis were true. Therefore, they retained the null hypothesis—concluding that there is no evidence of a sex difference in the population. We can also see why Kanner and his colleagues concluded that there is a correlation between hassles and symptoms in the population. They asked, “If the null hypothesis were true, how likely is it that we would find a strong correlation of +.60 in our sample?” Their answer to this question was that this sample relationship would be fairly unlikely if the null hypothesis were true. Therefore, they rejected the null hypothesis in favor of the alternative hypothesis—concluding that there is a positive correlation between these variables in the population.

A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value . A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A p value that is not low means that the sample result would be likely if the null hypothesis were true and leads to the retention of the null hypothesis. But how low must the p value be before the sample result is considered unlikely enough to reject the null hypothesis? In null hypothesis testing, this criterion is called α (alpha) and is almost always set to .05. If there is a 5% chance or less of a result as extreme as the sample result if the null hypothesis were true, then the null hypothesis is rejected. When this happens, the result is said to be statistically significant . If there is greater than a 5% chance of a result as extreme as the sample result when the null hypothesis is true, then the null hypothesis is retained. This does not necessarily mean that the researcher accepts the null hypothesis as true—only that there is not currently enough evidence to reject it. Researchers often use the expression “fail to reject the null hypothesis” rather than “retain the null hypothesis,” but they never use the expression “accept the null hypothesis.”

The Misunderstood p Value

“Null Hypothesis” retrieved from http://imgs.xkcd.com/comics/null_hypothesis.png (CC-BY-NC 2.5)

Role of Sample Size and Relationship Strength



Sample Size	Weak	Medium	Strong
Small ( = 20)	No	No	= Maybe = Yes
Medium ( = 50)	No	Yes	Yes
Large ( = 100)	= Yes = No	Yes	Yes
Extra large ( = 500)	Yes	Yes	Yes

Statistical Significance Versus Practical Significance

“Conditional Risk” retrieved from http://imgs.xkcd.com/comics/conditional_risk.png (CC-BY-NC 2.5)

Key Takeaways

Null hypothesis testing is a formal approach to deciding whether a statistical relationship in a sample reflects a real relationship in the population or is just due to chance.
The logic of null hypothesis testing involves assuming that the null hypothesis is true, finding how likely the sample result would be if this assumption were correct, and then making a decision. If the sample result would be unlikely if the null hypothesis were true, then it is rejected in favor of the alternative hypothesis. If it would not be unlikely, then the null hypothesis is retained.
The probability of obtaining the sample result if the null hypothesis were true (the p value) is based on two considerations: relationship strength and sample size. Reasonable judgments about whether a sample relationship is statistically significant can often be made by quickly considering these two factors.
Statistical significance is not the same as relationship strength or importance. Even weak relationships can be statistically significant if the sample size is large enough. It is important to consider relationship strength and the practical significance of a result in addition to its statistical significance.
Discussion: Imagine a study showing that people who eat more broccoli tend to be happier. Explain for someone who knows nothing about statistics why the researchers would conduct a null hypothesis test.
The correlation between two variables is r = −.78 based on a sample size of 137.
The mean score on a psychological characteristic for women is 25 ( SD = 5) and the mean score for men is 24 ( SD = 5). There were 12 women and 10 men in this study.
In a memory experiment, the mean number of items recalled by the 40 participants in Condition A was 0.50 standard deviations greater than the mean number recalled by the 40 participants in Condition B.
In another memory experiment, the mean scores for participants in Condition A and Condition B came out exactly the same!
A student finds a correlation of r = .04 between the number of units the students in his research methods class are taking and the students’ level of stress.
Cohen, J. (1994). The world is round: p < .05. American Psychologist, 49 , 997–1003. ↵
Hyde, J. S. (2007). New directions in the study of gender similarities and differences. Current Directions in Psychological Science, 16 , 259–263. ↵

Share This Book

Increase Font Size

Skip to secondary menu
Skip to main content
Skip to primary sidebar

Statistics By Jim

Making statistics intuitive

Failing to Reject the Null Hypothesis

By Jim Frost 69 Comments

Failing to reject the null hypothesis is an odd way to state that the results of your hypothesis test are not statistically significant. Why the peculiar phrasing? “Fail to reject” sounds like one of those double negatives that writing classes taught you to avoid. What does it mean exactly? There’s an excellent reason for the odd wording!

In this post, learn what it means when you fail to reject the null hypothesis and why that’s the correct wording. While accepting the null hypothesis sounds more straightforward, it is not statistically correct!

Before proceeding, let’s recap some necessary information. In all statistical hypothesis tests, you have the following two hypotheses:

The null hypothesis states that there is no effect or relationship between the variables.
The alternative hypothesis states the effect or relationship exists.

We assume that the null hypothesis is correct until we have enough evidence to suggest otherwise.

After you perform a hypothesis test, there are only two possible outcomes.

When your p-value is greater than your significance level, you fail to reject the null hypothesis. Your results are not significant. You’ll learn more about interpreting this outcome later in this post.

Related posts : Hypothesis Testing Overview and The Null Hypothesis

Why Don’t Statisticians Accept the Null Hypothesis?

To understand why we don’t accept the null, consider the fact that you can’t prove a negative. A lack of evidence only means that you haven’t proven that something exists. It does not prove that something doesn’t exist. It might exist, but your study missed it. That’s a huge difference and it is the reason for the convoluted wording. Let’s look at several analogies.

Species Presumed to be Extinct

Photograph of an Australian Tree Lobster.

Lack of proof doesn’t represent proof that something doesn’t exist!

Criminal Trials

Perhaps the prosecutor conducted a shoddy investigation and missed clues? Or, the defendant successfully covered his tracks? Consequently, the verdict in these cases is “not guilty.” That judgment doesn’t say the defendant is proven innocent, just that there wasn’t enough evidence to move the jury from the default assumption of innocence.

Hypothesis Tests

The Greek sympol of alpha, which represents the significance level.

The hypothesis test assesses the evidence in your sample. If your test fails to detect an effect, it’s not proof that the effect doesn’t exist. It just means your sample contained an insufficient amount of evidence to conclude that it exists. Like the species that were presumed extinct, or the prosecutor who missed clues, the effect might exist in the overall population but not in your particular sample. Consequently, the test results fail to reject the null hypothesis, which is analogous to a “not guilty” verdict in a trial. There just wasn’t enough evidence to move the hypothesis test from the default position that the null is true.

The critical point across these analogies is that a lack of evidence does not prove something does not exist—just that you didn’t find it in your specific investigation. Hence, you never accept the null hypothesis.

Related post : The Significance Level as an Evidentiary Standard

What Does Fail to Reject the Null Hypothesis Mean?

Accepting the null hypothesis would indicate that you’ve proven an effect doesn’t exist. As you’ve seen, that’s not the case at all. You can’t prove a negative! Instead, the strength of your evidence falls short of being able to reject the null. Consequently, we fail to reject it.

Failing to reject the null indicates that our sample did not provide sufficient evidence to conclude that the effect exists. However, at the same time, that lack of evidence doesn’t prove that the effect does not exist. Capturing all that information leads to the convoluted wording!

What are the possible implications of failing to reject the null hypothesis? Let’s work through them.

First, it is possible that the effect truly doesn’t exist in the population, which is why your hypothesis test didn’t detect it in the sample. Makes sense, right? While that is one possibility, it doesn’t end there.

Another possibility is that the effect exists in the population, but the test didn’t detect it for a variety of reasons. These reasons include the following:

The sample size was too small to detect the effect.
The variability in the data was too high. The effect exists, but the noise in your data swamped the signal (effect).
By chance, you collected a fluky sample. When dealing with random samples, chance always plays a role in the results. The luck of the draw might have caused your sample not to reflect an effect that exists in the population.

Notice how studies that collect a small amount of data or low-quality data are likely to miss an effect that exists? These studies had inadequate statistical power to detect the effect. We certainly don’t want to take results from low-quality studies as proof that something doesn’t exist!

However, failing to detect an effect does not necessarily mean a study is low-quality. Random chance in the sampling process can work against even the best research projects!

If you’re learning about hypothesis testing and like the approach I use in my blog, check out my eBook!

Cover image of my Hypothesis Testing: An Intuitive Guide ebook.

Reader Interactions

May 8, 2024 at 9:08 am

Thank you very much for explaining the topic. It brings clarity and makes statistics very simple and interesting. Its helping me in the field of Medical Research.

February 26, 2024 at 7:54 pm

Hi Jim, My question is that can I reverse Null hyposthesis and start with Null: µ1 ≠ µ2 ? Then, if I can reject Null, I will end up with µ1=µ2 for mean comparison and this what I am looking for. But isn’t this cheating?

February 26, 2024 at 11:41 pm

That can be done but it requires you to revamp the entire test. Keep in mind that the reason you normally start out with the null equating to no relationship is because the researchers typically want to prove that a relationship or effect exists. This format forces the researchers to collect a substantial amount of high quality data to have a chance at demonstrating that an effect exists. If they collect a small sample and/or poor quality (e.g., noisy or imprecise), then the results default back to the null stating that no effect exists. So, they have to collect good data and work hard to get findings that suggest the effect exists.

There are tests that flip it around as you suggest where the null states that a relationship does exist. For example, researchers perform an equivalency test when they want to show that there is no difference. That the groups are equal. The test is designed such that it requires a good sample size and high quality data to have a chance at proving equivalency. If they have a small sample size and/or poor quality data, the results default back to the groups being unequal, which is not what they want to show.

So, choose the null hypothesis and corresponding analysis based on what you hope to find. Choose the null hypothesis that forces you to work hard to reject it and get the results that you want. It forces you to collect better evidence to make your case and the results default back to what you don’t want if you do a poor job.

I hope that makes sense!

October 13, 2023 at 5:10 am

Really appreciate how you have been able to explain something difficult in very simple terms. Also covering why you can’t accept a null hypothesis – something which I think is frequently missed. Thank you, Jim.

February 22, 2022 at 11:18 am

Hi Jim, I really appreciate your blog, making difficult things sound simple is a great gift.

I have a doubt about the p-value. You said there are two options when it comes to hypothesis tests results . Reject or failing to reject the null, depending on the p-value and your significant level.

But… a P-value of 0,001 means a stronger evidence than a P-value of 0,01? ( both with a significant level of 5%. Or It doesn`t matter, and just every p-Value under your significant level means the same burden of evidence against the null?

I hope I made my point clear. Thanks a lot for your time.

February 23, 2022 at 9:06 pm

There are different schools of thought about this question. The traditional approach is clear cut. Your results are statistically significance when your p-value is less than or equal to your significance level. When the p-value is greater than the significance level, your results are not significant.

However, as you point out, lower p-values indicate stronger evidence against the null hypothesis. I write about this aspect of p-values in several articles, interpreting p-values (near the end) and p-values and reproducibility .

Personally, I consider both aspects. P-values near 0.05 provide weak evidence. Consequently, I’d be willing to say that p-values less than or equal to 0.05 are statistically significant, but when they’re near 0.05, I’d consider it as a preliminary result that requires more research. However, if the p-value is less 0.01, or even better 0.001, then that’s much stronger evidence and I’ll give those results more weight in my evaluation.

If you read those two articles, I think you’ll see what I mean.

January 1, 2022 at 6:00 pm

HI, I have a quick question that you may be able to help me with. I am using SPSS and carrying out a Mann W U Test it says to retain the null hypothesis. The hypothesis is that males are faster than women at completing a task. So is that saying that they are or are not

January 1, 2022 at 8:17 pm

In that case, your sample data provides insufficient evidence to conclude that males are faster. The results do not prove that males and females are the same speed. You just don’t have enough evidence to say males are faster. In this post, I cover the reasons why you can’t prove the null is true.

November 23, 2021 at 5:36 pm

What if I have to prove in my hypothesis that there shouldn’t be any affect of treatment on patients? Can I say that if my null hypothesis is accepted i have got my results (no effect)? I am confused what to do in this situation. As for null hypothesis we always have to write it with some type of equality. What if I want my result to be what i have stated in null hypothesis i.e. no effect? How to write statements in this case? I am using non parametric test, Mann whitney u test

November 27, 2021 at 4:56 pm

You need to perform an equivalence test, which is a special type of procedure when you want to prove that the results are equal. The problem with a regular hypothesis test is that when you fail to reject the null, you’re not proving that they the outcomes are equal. You can fail to reject the null thanks to a small sample size, noisy data, or a small effect size even when the outcomes are truly different at the population level. An equivalence test sets things up so you need strong evidence to really show that two outcomes are equal.

Unfortunately, I don’t have any content for equivalence testing at this point, but you can read an article about it at Wikipedia: Equivalence Test .

August 13, 2021 at 9:41 pm

Great explanation and great analogies! Thanks.

August 11, 2021 at 2:02 am

I got problems with analysis. I did wound healing experiments with drugs treatment (total 9 groups). When I do the 2-way ANOVA in excel, I got the significant results in sample (Drug Treatment) and columns (Day, Timeline) . But I did not get the significantly results in interactions. Can I still reject the null hypothesis and continue the post-hoc test?

Thank you very much.

June 13, 2021 at 4:51 am

Hi Jim, There are so many books covering maths/programming related to statistics/DS, but may be hardly any book to develop an intuitive understanding. Thanks to you for filling up that gap. After statistics, hypothesis-testing, regression, will it be possible for you to write such books on more topics in DS such as trees, deep-learning etc.

I recently started with reading your book on hypothesis testing (just finished the first chapter). I have a question w.r.t the fuel cost example (from first chapter), where a random sample of 25 families (with sample mean 330.6) is taken. To do the hypothesis testing here, we are taking a sampling distribution with a mean of 260. Then based on the p-value and significance level, we find whether to reject or accept the null hypothesis. The entire decision (to accept or reject the null hypothesis) is based on the sampling distribution about which i have the following questions : a) we are assuming that the sampling distribution is normally distributed. what if it has some other distribution, how can we find that ? b) We have assumed that the sampling distribution is normally distributed and then further assumed that its mean is 260 (as required for the hypothesis testing). But we need the standard deviation as well to define the normal distribution, can you please let me know how do we find the standard deviation for the sampling distribution ? Thanks.

April 24, 2021 at 2:25 pm

Maybe its the idea of “Innocent until proven guilty”? Your Null assume the person is not guilty, and your alternative assumes the person is guilty, only when you have enough evidence (finding statistical significance P0.05 you have failed to reject null hypothesis, null stands,implying the person is not guilty. Or, the person remain innocent.. Correct me if you think it’s wrong but this is the way I interpreted.

April 25, 2021 at 5:10 pm

I used the courtroom/trial analogy within this post. Read that for more details. I’d agree with your general take on the issue except when you have enough evidence you actually reject the null, which in the trial means the defendant is found guilty.

April 17, 2021 at 6:10 am

Can regression analysis be done using 5 companies variables for predicting working capital management and profitability positive/negative relationship?

Also, does null hypothesis rejecting means whatsoever is stated in null hypothesis that is false proved through regression analysis?

I have very less knowledge about regression analysis. Please help me, Sir. As I have my project report due on next week. Thanks in advance!

April 18, 2021 at 10:48 pm

Hi Ahmed, yes, regression analysis can be used for the scenario you describe as long as you have the required data.

For more about the null hypothesis in relation to regression analysis, read my post about regression coefficients and their p-values . I describe the null hypothesis in it.

January 26, 2021 at 7:32 pm

With regards to the legal example above. While your explanation makes sense when simplified to this statistical level, from a legal perspective it is not correct. The presumption of innocence means one does not need to be proven innocent. They are innocent. The onus of proof lies with proving they are guilty. So if you can’t prove someones guilt then in fact you must accept the null hypothesis that they are innocent. It’s not a statistical test so a little bit misleading using it an example, although I see why you would.

If it were a statistical test, then we would probably be rather paranoid that everyone is a murderer but they just haven’t been proven to be one yet.

Great article though, a nice simple and thoughtout explanation.

January 26, 2021 at 9:11 pm

It seems like you misread my post. The hypothesis testing/legal analogy is very strong both in making the case and in the result.

In hypothesis testing, the data have to show beyond a reasonable doubt that the alternative hypothesis is true. In a court case, the prosecutor has to present sufficient evidence to show beyond a reasonable doubt that the defendant is guilty.

In terms of the test/case results. When the evidence (data) is insufficient, you fail to reject the null hypothesis but you do not conclude that the data proves the null is true. In a legal case that has insufficient evidence, the jury finds the defendant to be “not guilty” but they do not say that s/he is proven innocent. To your point specifically, it is not accurate to say that “not guilty” is the same as “proven innocent.”

It’s a very strong parallel.

January 9, 2021 at 11:45 am

Just a question, in my research on hypotheses for an assignment, I am finding it difficult to find an exact definition for a hypothesis itself. I know the defintion, but I’m looking for a citable explanation, any ideas?

January 10, 2021 at 1:37 am

To be clear, do you need to come up with a statistical hypothesis? That’s one where you’ll use a particular statistical hypothesis test. If so, I’ll need to know more about what you’re studying, your variables, and the type of hypothesis test you plan to use.

There are also scientific hypotheses that you’ll state in your proposals, study papers, etc. Those are different from statistical hypotheses (although related). However, those are very study area specific and I don’t cover those types on this blog because this is a statistical blog. But, if it’s a statistical hypothesis for a hypothesis test, then let me know the information I mention above and I can help you out!

November 7, 2020 at 8:33 am

Hi, good read, I’m kind of a novice here, so I’m trying to write a research paper, and I’m trying to make a hypothesis. however looking at the literature, there are contradicting results.

researcher A found that there is relationship between X and Y

however, researcher B found that there is no relationship between X and Y

therefore, what is the null hypothesis between X and y? do we choose what we assumed to be correct for our study? or is is somehow related to the alternative hypothesis? I’m confused.

thank you very much for the help.

November 8, 2020 at 12:07 am

Hypotheses for a statistical test are different than a researcher’s hypothesis. When you’re constructing the statistical hypothesis, you don’t need to consider what other researchers have found. Instead, you construct them so that the test only produces statistically significant results (rejecting the null) when your data provides strong evidence. I talk about that process in this post.

Typically, researchers are hoping to establish that an effect or relationship exists. Consequently, the null and alternative hypotheses are typically the following:

Null: The effect or relationship doesn’t not exist. Alternative: The effect or relationship does exist.

However, if you’re hoping to prove that there is no effect or no relationship, you then need to flip those hypotheses and use a special test, such as an equivalences test.

So, there’s no need to consider what researchers have found but instead what you’re looking for. In most cases, you are looking for an effect/relationship, so you’d go with the hypotheses as I show them above.

I hope that helps!

October 22, 2020 at 6:13 pm

Great, deep detailed answer. Appreciated!

September 16, 2020 at 12:03 pm

Thank you for explaining it too clearly. I have the following situation with a Box Bohnken design of three levels and three factors for multiple responses. F-value for second order model is not significant (failing to reject null hypothesis, p-value > 0.05) but, lack of fit of the model is not significant. What can you suggest me about statistical analysis?

September 17, 2020 at 2:42 am

Are your first order effects significant?

You want the lack of fit to be nonsignificant. If it’s significant, that means the model doesn’t fit the data well. So, you’re good there! 🙂

September 14, 2020 at 5:18 pm

thank you for all the explicit explanation on the subject.

However, i still got a question about “accepting the null hypothesis”. from textbook, the p-value is the probability that a statistic would take a value that is as extreme as or more extreme than that actually observed.

so, that’s why when p<0.01 we reject the null hypothesis, because it's too rare (p0.05, i can understand that for most cases we cannot accept the null, for example, if p=0.5, it means that the probability to get a statistic from the distribution is 0.5, which is totally random.

But how about when the p is very close to 1, like p=0.95, or p=0.99999999, can’t we say that the probability that the statistic is not from this distribution is less than 0.05, | or in another way, the probability that the statistic is from the distribution is almost 1. can’t we accept the null in such circumstance?

September 11, 2020 at 12:14 pm

Wow! This is beautifully explained. “Lack of proof doesn’t represent proof that something doesn’t exist!”. This kinda, hit me with such force. Can I then, use the same analogy for many other things in life? LOL! 🙂

H0 = God does not exist; H1 = God does exist; WE fail to reject H0 as there is no evidence.

Thank you sir, this has answered many of my questions, statistically speaking! No pun intended with the above.

September 11, 2020 at 4:58 pm

Hi, LOL, I’m glad it had such meaning for you! I’ll leave the determination about the existence of god up to each person, but in general, yes, I think statistical thinking can be helpful when applied to real life. It is important to realize that lack of proof truly is not proof that something doesn’t exist. But, I also consider other statistical concepts, such as confounders and sampling methodology, to be useful keeping in mind when I’m considering everyday life stuff–even when I’m not statistically analyzing it. Those concepts are generally helpful when trying to figure out what is going on in your life! Are there other alternative explanations? Is what you’re perceiving likely to be biased by something that’s affecting the “data” you can observe? Am I drawing a conclusion based on a large or small sample? How strong is the evidence?

A lot of those concepts are great considerations even when you’re just informally assessing and draw conclusions about things happening in your daily life.

August 13, 2020 at 12:04 am

Dear Jim, thanks for clarifying. absolutely, now it makes sense. the topic is murky but it is good to have your guidance, and be clear. I have not come across an instructor as clear in explaining as you do. Appreciate your direction. Thanks a lot, Geetanjali

August 15, 2020 at 3:48 pm

Hi Geetanjali,

I’m glad my website is helpful! That makes my day hearing that. Thanks so much for writing!

August 12, 2020 at 9:37 am

Hi Jim. I am doing data analyis for my masters thesis and my hypothesis testings were insignificant. And I am ok with that. But there is something bothering me. It is the low reliabilities of the 4-Items sub-scales (.55, .68, .75), though the overall alpha is good (.85). I just wonder if it is affecting my hypothesis testings.

August 11, 2020 at 9:23 pm

Thank you sir for replying, yes sir we it’s a RCT study.. where we did within and between the groups analysis and found p>0.05 in between the groups using Mann Whitney U test. So in such cases if the results comes like this we need to Mention that we failed reject the null hypothesis? Is that correct? Whether it tells that the study is inefficient as we couldn’t accept the alternative hypothesis. Thanks is advance.

August 11, 2020 at 9:43 pm

Hi Saumya, ah, this becomes clearer. When ask statistical questions, please be sure to include all relevant information because the details are extremely important. I didn’t know it was an RCT with a treatment and control group. Yes, given that your p-value is greater than your significance level, you fail to reject the null hypothesis. The results are not significant. The experiment provides insufficient evidence to conclude that the outcome in the treatment group is different than the control group.

By the way, you never accept the alternative hypothesis (or the null). The two options are to either reject the null or fail to reject the null. In your case, you fail to reject the null hypothesis.

I hope this helps!

August 11, 2020 at 9:41 am

Sir, p value is0.05, by which we interpret that both the groups are equally effective. In this case I had to reject the alternative hypothesis/ failed to reject null hypothessis.

August 11, 2020 at 12:37 am

sir, within the group analysis the p value for both the groups is significant (p0.05, by which we interpret that though both the treatments are effective, there in no difference between the efficacy of one over the other.. in other words.. no intervention is superior and both are equally effective.

August 11, 2020 at 2:45 pm

Thanks for the additional details. If I understand correctly, there were separate analyses before that determined each treatment had a statistically significance effect. However, when you compare the two treatments, there difference between them is not statistically significant.

If that’s the case, the interpretation is fairly straightforward. You have evidence that suggests that both treatments are effective. However, you don’t have evidence to conclude that one is better than the other.

August 10, 2020 at 9:26 am

Hi thank you for a wonderful explanation. I have a doubt: My Null hypothesis says: no significant difference between the effect fo A and B treatment Alternative hypothesis: there will be significant difference between the effect of A and B treatment. and my results show that i fail to reject null hypothesis.. Both the treatments were effective, but not significant difference.. how do I interpret this?

August 10, 2020 at 1:32 pm

First, I need to ask you a question. If your p-value is not significant, and so you fail to reject the null, why do you say that the treatment is effective? I can answer you question better after knowing the reason you say that. Thanks!

August 9, 2020 at 9:40 am

Dear Jim, thanks for making stats much more understandable and answering all question so painstakingly. I understand the following on p value and null. If our sample yields a p value of .01, it means that that there is a 1% probability that our kind of sample exists in the population. that is a rare event. So why shouldn’t we accept the HO as the probability of our event was v rare. Pls can you correct me. Thanks, G

August 10, 2020 at 1:53 pm

That’s a great question! They key thing to remember is that p-values are a conditional probability. P-value calculations assume that the null hypothesis is true. So, a p-value of 0.01 indicates that there is a 1% probability of observing your sample results, or more extreme, *IF* the null hypothesis is true.

The kicker is that we don’t whether the null is true or not. But, using this process does limit the likelihood of a false positive to your significance level (alpha). But, we don’t know whether the null is true and you had an unusual sample or whether the null is false. Usually, with a p-value of 0.01, we’d reject the null and conclude it is false.

I hope that answered your question. This topic can be murky and I wasn’t quite clear which part you needed clarification.

August 4, 2020 at 11:16 pm

Thank you for the wonderful explanation. However, I was just curious to know that what if in a particular test, we get a p-value less than the level of significance, leading to evidence against null hypothesis. Is there any possibility that our interpretation of population effect might be wrong due to randomness of samples? Also, how do we conclude whether the evidence is enough for our alternate hypothesis?

August 4, 2020 at 11:55 pm

Hi Abhilash,

Yes, unfortunately, when you’re working with samples, there’s always the possibility that random chance will cause your sample to not represent the population. For information about these errors, read my post about the types of errors in hypothesis testing .

In hypothesis testing, you determine whether your evidence is strong enough to reject the null. You don’t accept the alternative hypothesis. I cover that in my post about interpreting p-values .

August 1, 2020 at 3:50 pm

Hi, I am trying to interpret this phenomenon after my research. The null hypothesis states that “The use of combined drugs A and B does not lower blood pressure when compared to if drug A or B is used singularly”

The alternate hypothesis states: The use of combined drugs A and B lower blood pressure compared to if drug A or B is used singularly.

At the end of the study, majority of the people did not actually combine drugs A and B, rather indicated they either used drug A or drug B but not a combination. I am finding it very difficult to explain this outcome more so that it is a descriptive research. Please how do I go about this? Thanks a lot

June 22, 2020 at 10:01 am

What confuses me is how we set/determine the null hypothesis? For example stating that two sets of data are either no different or have no relationship will give completely different outcomes, so which is correct? Is the null that they are different or the same?

June 22, 2020 at 2:16 pm

Typically, the null states there is no effect/no relationship. That’s true for 99% of hypothesis tests. However, there are some equivalence tests where you are trying to prove that the groups are equal. In that case, the null hypothesis states that groups are not equal.

The null hypothesis is typically what you *don’t* want to find. You have to work hard, design a good experiment, collect good data, and end up with sufficient evidence to favor the alternative hypothesis. Usually in an experiment you want to find an effect. So, usually the null states there is no effect and you have get good evidence to reject that notion.

However, there are a few tests where you actually want to prove something is equal, so you need the null to state that they’re not equal in those cases and then do all the hard work and gather good data to suggest that they are equal. Basically, set up the hypothesis so it takes a good experiment and solid evidence to be able to reject the null and favor the hypothesis that you’re hoping is true.

June 5, 2020 at 11:54 am

Thank you for the explanation. I have one question that. If Null hypothesis is failed to reject than is possible to interpret the analysis further?

June 5, 2020 at 7:36 pm

Hi Mottakin,

Typically, if your result is that you fail to reject the null hypothesis there’s not much further interpretation. You don’t want to be in a situation where you’re endlessly trying new things on a quest for obtaining significant results. That’s data mining.

May 25, 2020 at 7:55 am

I hope all is well. I am enjoying your blog. I am not a statistician, however, I use statistical formulae to provide insight on the direction in which data is going. I have used both the regression analysis and a T-Test. I know that both use a null hypothesis and an alternative hypothesis. Could you please clarity the difference between a regression analysis and a T-Test? Are there conditions where one is a better option than the other?

May 26, 2020 at 9:18 pm

t-Tests compare the means of one or two groups. Regression analysis typically describes the relationships between a set of independent variables and the dependent variables. Interestingly, you can actually use regression analysis to perform a t-test. However, that would be overkill. If you just want to compare the means of one or two groups, use a t-test. Read my post about performing t-tests in Excel to see what they can do. If you have a more complex model than just comparing one or two means, regression might be the way to go. Read my post about when to use regression analysis .

May 12, 2020 at 5:45 pm

This article is really enlightening but there is still some darkness looming around. I see that low p-values mean strong evidence against null hypothesis and finding such a sample is highly unlikely when null hypothesis is true. So , is it OK to say that when p-value is 0.01 , it was very unlikely to have found such a sample but we still found it and hence finding such a sample has not occurred just by chance which leads towards rejection of null hypothesis.

May 12, 2020 at 11:16 pm

That’s mostly correct. I wouldn’t say, “has not occurred by chance.” So, when you get a very low p-value it does mean that you are unlikely to obtain that sample if the null is true. However, once you obtain that result, you don’t know for sure which of the two occurred:

The effect exists in the population.
Random chance gave you an unusual sample (i.e., Type I error).

You really don’t know for sure. However, by the decision making results you set about the strength of evidence required to reject the null, you conclude that the effect exists. Just always be aware that it could be a false positive.

That’s all a long way of saying that your sample was unlikely to occur by chance if the null is true.

April 29, 2020 at 11:59 am

Why do we consult the statistical tables to find out the critical values of our test statistics?

April 30, 2020 at 5:05 pm

Statistical tables started back in the “olden days” when computers didn’t exist. You’d calculate the test statistic value for your sample. Then, you’d look in the appropriate table and using the degrees of freedom for your design and find the critical values for the test statistic. If the value of your test statistics exceeded the critical value, your results were statistically significant.

With powerful and readily available computers, researchers could analyze their data and calculate the p-values and compare them directly to the significance level.

I hope that answers your question!

April 15, 2020 at 10:12 am

If we are not able to reject the null hypothesis. What could be the solution?

April 16, 2020 at 11:13 pm

Hi Shazzad,

The first thing to recognize is that failing to reject the null hypothesis might not be an error. If the null hypothesis is false, then the correct outcome is failing to reject the null.

However, if the null hypothesis is false and you fail to reject, it is a type II error, or a false negative. Read my post about types of errors in hypothesis tests for more information.

This type of error can occur for a variety of reasons, including the following:

Fluky sample. When working with random samples, random error can cause anomalous results purely by chance.
Sample is too small. Perhaps the sample was too small, which means the test didn’t have enough statistical power to detect the difference.
Problematic data or sampling methodology. There could be a problem with how you collected the data or your sampling methodology.

There are various other possibilities, but those are several common problems.

April 14, 2020 at 12:19 pm

Thank you so much for this article! I am taking my first Statistics class in college and I have one question about this.

I understand that the default position is that the null is correct, and you explained that (just like a court case), the sample evidence must EXCEED the “evidentiary standard” (which is the significance level) to conclude that an effect/relationship exists. And, if an effect/relationship exists, that means that it’s the alternative hypothesis that “wins” (not sure if that’s the correct way of wording it, but I’m trying to make this as simple as possible in my head!).

But what I don’t understand is that if the P-value is GREATER than the significance value, we fail to reject the null….because shouldn’t a higher P-value, mean that our sample evidence EXCEEDS the evidentiary standard (aka the significance level), and therefore an effect/relationship exists? In my mind it would make more sense to reject the null, because our P-value is higher and therefore we have enough evidence to reject the null.

I hope I worded this in a way that makes sense. Thank you in advance!

April 14, 2020 at 10:42 pm

That’s a great question. The key thing to remember is that higher p-values correspond to weaker evidence against the null hypothesis. A high p-value indicates that your sample is likely (high probability = high p-value) if the null hypothesis is true. Conversely, low p-values represent stronger evidence against the null. You were unlikely (low probability = low p-value) to have collect a sample with the measured characteristics if the null is true.

So, there is negative correlation between p-values and strength of evidence against the null hypothesis. Low p-values indicate stronger evidence. Higher p-value represent weaker evidence.

In a nutshell, you reject the null hypothesis with a low p-value because it indicates your sample data are unusual if the null is true. When it’s unusual enough, you reject the null.

March 5, 2020 at 11:10 am

There is something I am confused about. If our significance level is .05 and our resulting p-value is .02 (thus the strength of our evidence is strong enough to reject the null hypothesis), do we state that we reject the null hypothesis with 95% confidence or 98% confidence?

My guess is our confidence level is 95% since or alpha was .05. But if the strength of our evidence is 98%, why wouldn’t we use that as our stated confidence in our results?

March 5, 2020 at 4:19 pm

Hi Michael,

You’d state that you can reject the null at a significance level of 5% or conversely at the 95% confidence level. A key reason is to avoid cherry picking your results. In other words, you don’t want to choose the significance level based on your results.

Consequently, set the significance level/confidence level before performing your analysis. Then, use those preset levels to determine statistical significance. I always recommend including the exact p-value when you report on statistical significance. Exact p-values do provide information about the strength of evidence against the null.

March 5, 2020 at 9:58 am

Thank you for sharing this knowledge , it is very appropriate in explaining some observations in the study of forest biodiversity.

March 4, 2020 at 2:01 am

Thank you so much. This provides for my research

March 3, 2020 at 7:28 pm

If one couples this with what they call estimated monetary value of risk in risk management, one can take better decisions.

March 3, 2020 at 3:12 pm

Thank you for providing this clear insight.

March 3, 2020 at 3:29 am

Nice article Jim. The risk of such failure obviously reduces when a lower significance level is specified.One benefits most by reading this article in conjunction with your other article “Understanding Significance Levels in Statistics”.

March 3, 2020 at 2:43 am

That’s fine. My question is why doesn’t the numerical value of type 1 error coincide with the significance level in the backdrop that the type 1 error and the significance level are both the same ? I hope you got my question.

March 3, 2020 at 3:30 am

Hi, they are equal. As I indicated, the significance level equals the type I error rate.

March 3, 2020 at 1:27 am

Kindly elighten me on one confusion. We set out our significance level before setting our hypothesis. When we calculate the type 1 error, which happens to be a significance level, the numerical value doesn’t equals (either undermining value comes out or an exceeding value comescout ) our significance level that was preassigned. Why is this so ?

March 3, 2020 at 2:24 am

Hi Ratnadeep,

You’re correct. The significance level (alpha) is the same as the type I error rate. However, you compare the p-value to the significance level. It’s the p-value that can be greater than or less than the significance level.

The significance level is the evidentiary standard. How strong does the evidence in your sample need to be before you can reject the null? The p-value indicates the strength of the evidence that is present in your sample. By comparing the p-value to the significance level, you’re comparing the actual strength of the sample evidence to the evidentiary standard to determine whether your sample evidence is strong enough to conclude that the effect exists in the population.

I write about this in my post about the understanding significance levels . I think that will help answer your questions!

Comments and Questions Cancel reply

9.1 Null and Alternative Hypotheses

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 , the — null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.

H a —, the alternative hypothesis: a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are reject H 0 if the sample information favors the alternative hypothesis or do not reject H 0 or decline to reject H 0 if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in H 0 and H a :


equal (=)	not equal (≠) greater than (>) less than (<)
greater than or equal to (≥)	less than (<)
less than or equal to (≤)	more than (>)

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example 9.1

H 0 : No more than 30 percent of the registered voters in Santa Clara County voted in the primary election. p ≤ 30 H a : More than 30 percent of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25 percent. State the null and alternative hypotheses.

Example 9.2

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are the following: H 0 : μ = 2.0 H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

H 0 : μ __ 66
H a : μ __ 66

Example 9.3

We want to test if college students take fewer than five years to graduate from college, on the average. The null and alternative hypotheses are the following: H 0 : μ ≥ 5 H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

H 0 : μ __ 45
H a : μ __ 45

Example 9.4

An article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third of the students pass. The same article stated that 6.6 percent of U.S. students take advanced placement exams and 4.4 percent pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6 percent. State the null and alternative hypotheses. H 0 : p ≤ 0.066 H a : p > 0.066

On a state driver’s test, about 40 percent pass the test on the first try. We want to test if more than 40 percent pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

H 0 : p __ 0.40
H a : p __ 0.40

Collaborative Exercise

Bring to class a newspaper, some news magazines, and some internet articles. In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-statistics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/statistics/pages/1-introduction

Authors: Barbara Illowsky, Susan Dean
Publisher/website: OpenStax
Book title: Statistics
Publication date: Mar 27, 2020
Location: Houston, Texas
Book URL: https://openstax.org/books/statistics/pages/1-introduction
Section URL: https://openstax.org/books/statistics/pages/9-1-null-and-alternative-hypotheses

© Apr 16, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

User Preferences

Content preview.

Arcu felis bibendum ut tristique et egestas quis:

Ut enim ad minim veniam, quis nostrud exercitation ullamco laboris
Duis aute irure dolor in reprehenderit in voluptate
Excepteur sint occaecat cupidatat non proident

Keyboard Shortcuts

S.3.1 hypothesis testing (critical value approach).

The critical value approach involves determining "likely" or "unlikely" by determining whether or not the observed test statistic is more extreme than would be expected if the null hypothesis were true. That is, it entails comparing the observed test statistic to some cutoff value, called the " critical value ." If the test statistic is more extreme than the critical value, then the null hypothesis is rejected in favor of the alternative hypothesis. If the test statistic is not as extreme as the critical value, then the null hypothesis is not rejected.

Specifically, the four steps involved in using the critical value approach to conducting any hypothesis test are:

Specify the null and alternative hypotheses.
Using the sample data and assuming the null hypothesis is true, calculate the value of the test statistic. To conduct the hypothesis test for the population mean μ , we use the t -statistic $t^*=\frac{\bar{x}-\mu}{s/\sqrt{n}}$ which follows a t -distribution with n - 1 degrees of freedom.
Determine the critical value by finding the value of the known distribution of the test statistic such that the probability of making a Type I error — which is denoted $\alpha$ (greek letter "alpha") and is called the " significance level of the test " — is small (typically 0.01, 0.05, or 0.10).
Compare the test statistic to the critical value. If the test statistic is more extreme in the direction of the alternative than the critical value, reject the null hypothesis in favor of the alternative hypothesis. If the test statistic is less extreme than the critical value, do not reject the null hypothesis.

Example S.3.1.1

Mean gpa section .

In our example concerning the mean grade point average, suppose we take a random sample of n = 15 students majoring in mathematics. Since n = 15, our test statistic t * has n - 1 = 14 degrees of freedom. Also, suppose we set our significance level α at 0.05 so that we have only a 5% chance of making a Type I error.

Right-Tailed

The critical value for conducting the right-tailed test H 0 : μ = 3 versus H A : μ > 3 is the t -value, denoted t $\alpha$ , n - 1 , such that the probability to the right of it is $\alpha$. It can be shown using either statistical software or a t -table that the critical value t 0.05,14 is 1.7613. That is, we would reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ > 3 if the test statistic t * is greater than 1.7613. Visually, the rejection region is shaded red in the graph.

t distribution graph for a t value of 1.76131

Left-Tailed

The critical value for conducting the left-tailed test H 0 : μ = 3 versus H A : μ < 3 is the t -value, denoted -t ( $\alpha$ , n - 1) , such that the probability to the left of it is $\alpha$. It can be shown using either statistical software or a t -table that the critical value -t 0.05,14 is -1.7613. That is, we would reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ < 3 if the test statistic t * is less than -1.7613. Visually, the rejection region is shaded red in the graph.

There are two critical values for the two-tailed test H 0 : μ = 3 versus H A : μ ≠ 3 — one for the left-tail denoted -t ( $\alpha$ / 2, n - 1) and one for the right-tail denoted t ( $\alpha$ / 2, n - 1) . The value - t ( $\alpha$ /2, n - 1) is the t -value such that the probability to the left of it is $\alpha$/2, and the value t ( $\alpha$ /2, n - 1) is the t -value such that the probability to the right of it is $\alpha$/2. It can be shown using either statistical software or a t -table that the critical value -t 0.025,14 is -2.1448 and the critical value t 0.025,14 is 2.1448. That is, we would reject the null hypothesis H 0 : μ = 3 in favor of the alternative hypothesis H A : μ ≠ 3 if the test statistic t * is less than -2.1448 or greater than 2.1448. Visually, the rejection region is shaded red in the graph.

t distribution graph for a two tailed test of 0.05 level of significance

Hypothesis Testing with Z-Test: Significance Level and Rejection Region

Join over 2 million students who advanced their careers with 365 Data Science. Learn from instructors who have worked at Meta, Spotify, Google, IKEA, Netflix, and Coca-Cola and master Python, SQL, Excel, machine learning, data analysis, AI fundamentals, and more.

If you want to understand why hypothesis testing works, you should first have an idea about the significance level and the reject region . We assume you already know what a hypothesis is , so let’s jump right into the action.

What Is the Significance Level?

First, we must define the term significance level .

Normally, we aim to reject the null if it is false.

However, as with any test, there is a small chance that we could get it wrong and reject a null hypothesis that is true.

How Is the Significance Level Denoted?

The significance level is denoted by α and is the probability of rejecting the null hypothesis , if it is true.

α and is the probability of rejecting the null hypothesis, significance level

So, the probability of making this error.

Typical values for α are 0.01, 0.05 and 0.1. It is a value that we select based on the certainty we need. In most cases, the choice of α is determined by the context we are operating in, but 0.05 is the most commonly used value.

A Case in Point

Say, we need to test if a machine is working properly. We would expect the test to make little or no mistakes. As we want to be very precise, we should pick a low significance level such as 0.01.

The famous Coca Cola glass bottle is 12 ounces. If the machine pours 12.1 ounces, some of the liquid would be spilled, and the label would be damaged as well. So, in certain situations, we need to be as accurate as possible.

Higher Degree of Error

However, if we are analyzing humans or companies, we would expect more random or at least uncertain behavior. Hence, a higher degree of error.

You expect more random behavior, significance level

For instance, if we want to predict how much Coca Cola its consumers drink on average, the difference between 12 ounces and 12.1 ounces will not be that crucial. So, we can choose a higher significance level like 0.05 or 0.1.

The difference between 12 and 12.1, significance level

Hypothesis Testing: Performing a Z-Test

Now that we have an idea about the significance level , let’s get to the mechanics of hypothesis testing.

Imagine you are consulting a university and want to carry out an analysis on how students are performing on average.

How students are performing on average, significance-level

The university dean believes that on average students have a GPA of 70%. Being the data-driven researcher that you are, you can’t simply agree with his opinion, so you start testing.

The null hypothesis is: The population mean grade is 70%.

This is a hypothesized value.

The alternative hypothesis is: The population mean grade is not 70%. You can see how both of them are denoted, below.

University Dean example: Null hypothesis equals the population mean

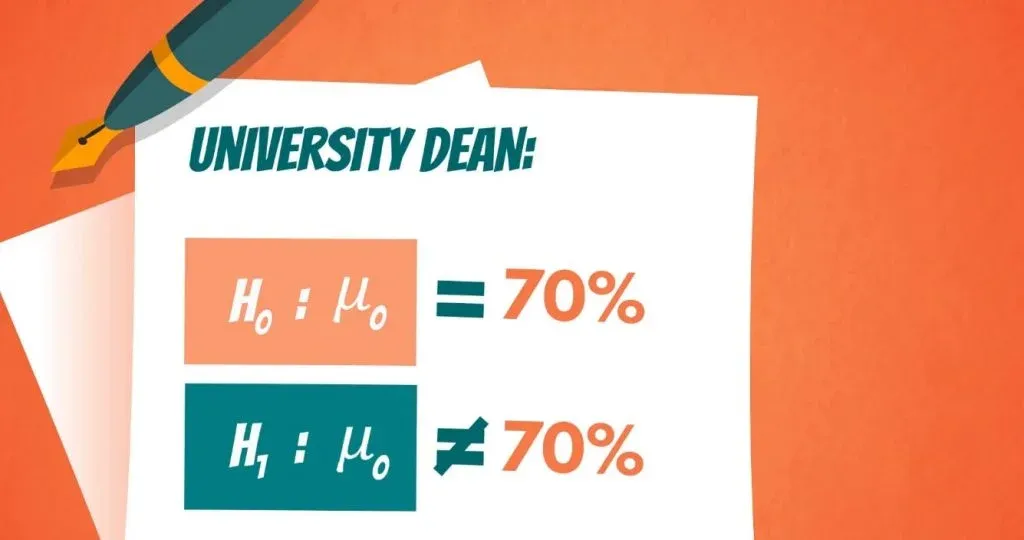
Visualizing the Grades

Assuming that the population of grades is normally distributed, all grades received by students should look in the following way.

Distribution of grades, significance level

That is the true population mean .

Performing a Z-test

Now, a test we would normally perform is the Z-test . The formula is:

Z equals the sample mean , minus the hypothesized mean , divided by the standard error .

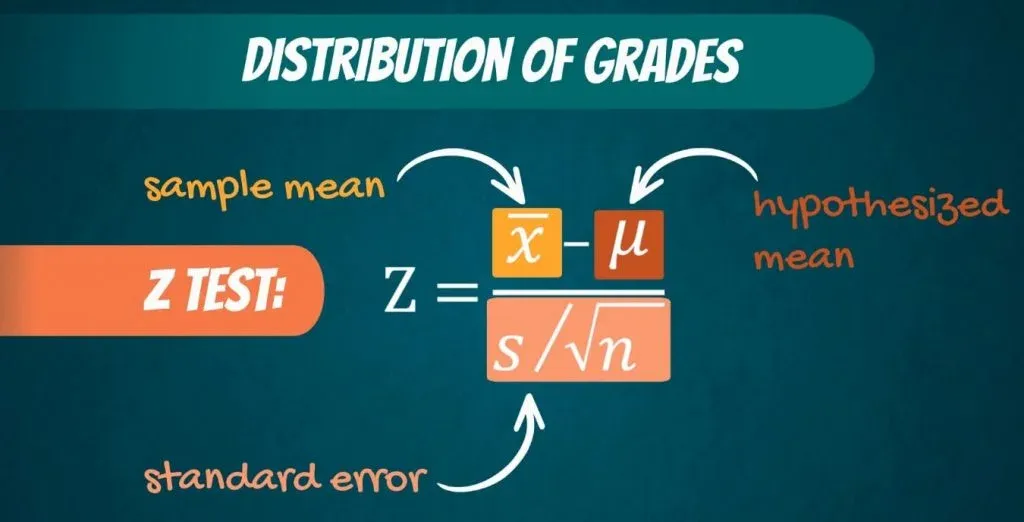
The idea is the following.

We are standardizing or scaling the sample mean we got. (You can quickly obtain it with our Mean, Median, Mode calculator .) If the sample mean is close enough to the hypothesized mean , then Z will be close to 0. Otherwise, it will be far away from it. Naturally, if the sample mean is exactly equal to the hypothesized mean , Z will be 0.

If the sample mean is exactly equal to the hypothesized mean, Z will be 0, significance level

In all these cases, we would accept the null hypothesis .

What Is the Rejection Region?

The question here is the following:

How big should Z be for us to reject the null hypothesis ?

Well, there is a cut-off line. Since we are conducting a two-sided or a two-tailed test, there are two cut-off lines, one on each side.

Distribution of Z (standard normal distribution), significance level

When we calculate Z , we will get a value. If this value falls into the middle part, then we cannot reject the null. If it falls outside, in the shaded region, then we reject the null hypothesis .

That is why the shaded part is called: rejection region , as you can see below.

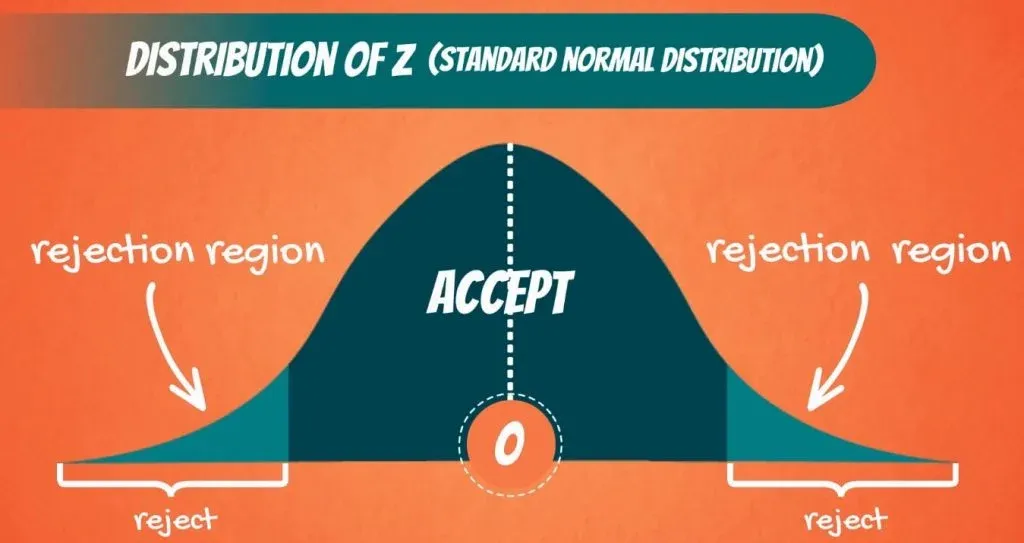
What Does the Rejection Region Depend on?

The area that is cut-off actually depends on the significance level .

Say the level of significance , α , is 0.05. Then we have α divided by 2, or 0.025 on the left side and 0.025 on the right side.

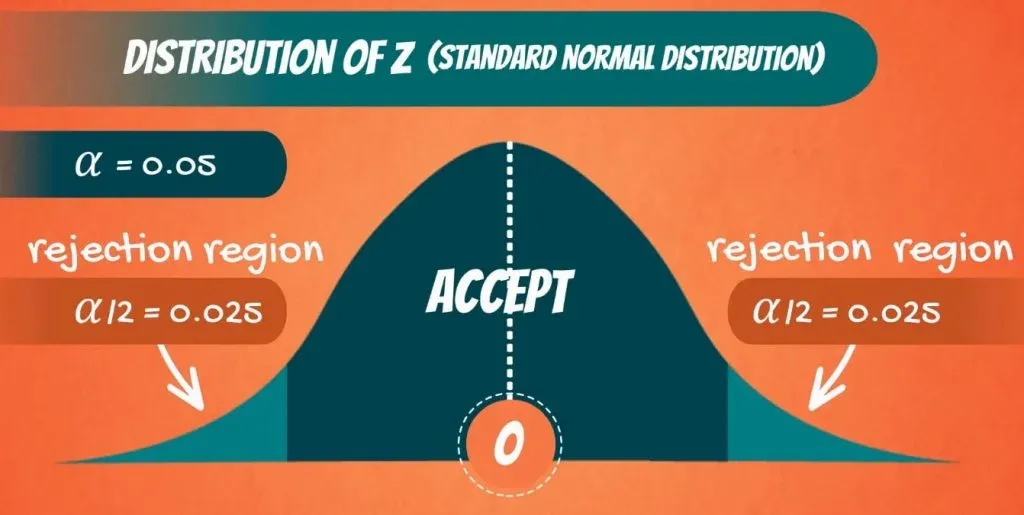
Now these are values we can check from the z-table . When α is 0.025, Z is 1.96. So, 1.96 on the right side and minus 1.96 on the left side.

Therefore, if the value we get for Z from the test is lower than minus 1.96, or higher than 1.96, we will reject the null hypothesis . Otherwise, we will accept it.

That’s more or less how hypothesis testing works.

We scale the sample mean with respect to the hypothesized value. If Z is close to 0, then we cannot reject the null. If it is far away from 0, then we reject the null hypothesis .

Example of One Tailed Test

What about one-sided tests? We have those too!

Let’s consider the following situation.

Paul says data scientists earn more than $125,000. So, H 0 is: μ 0 is bigger than $125,000.

The alternative is that μ 0 is lower or equal to 125,000.

Using the same significance level , this time, the whole rejection region is on the left. So, the rejection region has an area of α . Looking at the z-table, that corresponds to a Z -score of 1.645. Since it is on the left, it is with a minus sign.

Accept or Reject

Now, when calculating our test statistic Z , if we get a value lower than -1.645, we would reject the null hypothesis . We do that because we have statistical evidence that the data scientist salary is less than $125,000. Otherwise, we would accept it.

One-sided test: Z score is - 1.645 - rejecting null hypothesis

Another One-Tailed Test

To exhaust all possibilities, let’s explore another one-tailed test.

Say the university dean told you that the average GPA students get is lower than 70%. In that case, the null hypothesis is:

μ 0 is lower than 70%.

While the alternative is:

μ 0` is bigger or equal to 70%.

University Dean example: Null hypothesis lower than the population mean

In this situation, the rejection region is on the right side. So, if the test statistic is bigger than the cut-off z-score, we would reject the null, otherwise, we wouldn’t.

One-sided test: test statistic is bigger than the cut-off z-score - reject the null hypothesis

Importance of the Significance Level and the Rejection Region

To sum up, the significance level and the reject region are quite crucial in the process of hypothesis testing. The level of significance conducts the accuracy of prediction. We (the researchers) choose it depending on how big of a difference a possible error could make. On the other hand, the reject region helps us decide whether or not to reject the null hypothesis . After reading this and putting both of them into use, you will realize how convenient they make your work.

Interested in taking your skills from good to great? Try statistics course for free !

Next Tutorial: Providing a Few Linear Regression Examples

Iliya Valchanov

Co-founder of 365 Data Science

Iliya is a finance graduate with a strong quantitative background who chose the exciting path of a startup entrepreneur. He demonstrated a formidable affinity for numbers during his childhood, winning more than 90 national and international awards and competitions through the years. Iliya started teaching at university, helping other students learn statistics and econometrics. Inspired by his first happy students, he co-founded 365 Data Science to continue spreading knowledge. He authored several of the program’s online courses in mathematics, statistics, machine learning, and deep learning.

We Think you'll also like

Statistics Tutorials

Hypothesis Testing: Null Hypothesis and Alternative Hypothesis

False Positive vs. False Negative: Type I and Type II Errors in Statistical Hypothesis Testing

Calculating and Using Covariance and Linear Correlation Coefficient

Examples of Numerical and Categorical Variables

Hypothesis Testing for Means & Proportions

1
| 2
| 3
| 4
| 5
| 6
| 7
| 8
| 9
| 10

Hypothesis Testing: Upper-, Lower, and Two Tailed Tests

Type i and type ii errors.

All Modules

Z score Table

t score Table

The procedure for hypothesis testing is based on the ideas described above. Specifically, we set up competing hypotheses, select a random sample from the population of interest and compute summary statistics. We then determine whether the sample data supports the null or alternative hypotheses. The procedure can be broken down into the following five steps.

Step 1. Set up hypotheses and select the level of significance α.

H 0 : Null hypothesis (no change, no difference);

H 1 : Research hypothesis (investigator's belief); α =0.05

Upper-tailed, Lower-tailed, Two-tailed Tests

The research or alternative hypothesis can take one of three forms. An investigator might believe that the parameter has increased, decreased or changed. For example, an investigator might hypothesize:

: μ > μ , where μ is the comparator or null value (e.g., μ =191 in our example about weight in men in 2006) and an increase is hypothesized - this type of test is called an ; : μ < μ , where a decrease is hypothesized and this is called a ; or : μ ≠ μ where a difference is hypothesized and this is called a .

The exact form of the research hypothesis depends on the investigator's belief about the parameter of interest and whether it has possibly increased, decreased or is different from the null value. The research hypothesis is set up by the investigator before any data are collected.

Step 2. Select the appropriate test statistic.

The test statistic is a single number that summarizes the sample information. An example of a test statistic is the Z statistic computed as follows:

When the sample size is small, we will use t statistics (just as we did when constructing confidence intervals for small samples). As we present each scenario, alternative test statistics are provided along with conditions for their appropriate use.

Step 3. Set up decision rule.

The decision rule is a statement that tells under what circumstances to reject the null hypothesis. The decision rule is based on specific values of the test statistic (e.g., reject H 0 if Z > 1.645). The decision rule for a specific test depends on 3 factors: the research or alternative hypothesis, the test statistic and the level of significance. Each is discussed below.

The decision rule depends on whether an upper-tailed, lower-tailed, or two-tailed test is proposed. In an upper-tailed test the decision rule has investigators reject H 0 if the test statistic is larger than the critical value. In a lower-tailed test the decision rule has investigators reject H 0 if the test statistic is smaller than the critical value. In a two-tailed test the decision rule has investigators reject H 0 if the test statistic is extreme, either larger than an upper critical value or smaller than a lower critical value.
The exact form of the test statistic is also important in determining the decision rule. If the test statistic follows the standard normal distribution (Z), then the decision rule will be based on the standard normal distribution. If the test statistic follows the t distribution, then the decision rule will be based on the t distribution. The appropriate critical value will be selected from the t distribution again depending on the specific alternative hypothesis and the level of significance.
The third factor is the level of significance. The level of significance which is selected in Step 1 (e.g., α =0.05) dictates the critical value. For example, in an upper tailed Z test, if α =0.05 then the critical value is Z=1.645.

The following figures illustrate the rejection regions defined by the decision rule for upper-, lower- and two-tailed Z tests with α=0.05. Notice that the rejection regions are in the upper, lower and both tails of the curves, respectively. The decision rules are written below each figure.

Rejection Region for Upper-Tailed Z Test (H : μ > μ ) with α=0.05

The decision rule is: Reject H if Z 1.645.


α	Z
0.10	1.282
0.05	1.645
0.025	1.960
0.010	2.326
0.005	2.576
0.001	3.090
0.0001	3.719

Standard normal distribution with lower tail at -1.645 and alpha=0.05

Rejection Region for Lower-Tailed Z Test (H 1 : μ < μ 0 ) with α =0.05

The decision rule is: Reject H 0 if Z < 1.645.


a	Z
0.10	-1.282
0.05	-1.645
0.025	-1.960
0.010	-2.326
0.005	-2.576
0.001	-3.090
0.0001	-3.719

Standard normal distribution with two tails

Rejection Region for Two-Tailed Z Test (H 1 : μ ≠ μ 0 ) with α =0.05

The decision rule is: Reject H 0 if Z < -1.960 or if Z > 1.960.



0.20	1.282
0.10	1.645
0.05	1.960
0.010	2.576
0.001	3.291
0.0001	3.819

The complete table of critical values of Z for upper, lower and two-tailed tests can be found in the table of Z values to the right in "Other Resources."

Critical values of t for upper, lower and two-tailed tests can be found in the table of t values in "Other Resources."

Step 4. Compute the test statistic.

Here we compute the test statistic by substituting the observed sample data into the test statistic identified in Step 2.

Step 5. Conclusion.

The final conclusion is made by comparing the test statistic (which is a summary of the information observed in the sample) to the decision rule. The final conclusion will be either to reject the null hypothesis (because the sample data are very unlikely if the null hypothesis is true) or not to reject the null hypothesis (because the sample data are not very unlikely).

If the null hypothesis is rejected, then an exact significance level is computed to describe the likelihood of observing the sample data assuming that the null hypothesis is true. The exact level of significance is called the p-value and it will be less than the chosen level of significance if we reject H 0 .

Statistical computing packages provide exact p-values as part of their standard output for hypothesis tests. In fact, when using a statistical computing package, the steps outlined about can be abbreviated. The hypotheses (step 1) should always be set up in advance of any analysis and the significance criterion should also be determined (e.g., α =0.05). Statistical computing packages will produce the test statistic (usually reporting the test statistic as t) and a p-value. The investigator can then determine statistical significance using the following: If p < α then reject H 0 .

Step 1. Set up hypotheses and determine level of significance

H 0 : μ = 191 H 1 : μ > 191 α =0.05

The research hypothesis is that weights have increased, and therefore an upper tailed test is used.

Step 2. Select the appropriate test statistic.

Because the sample size is large (n > 30) the appropriate test statistic is

Step 3. Set up decision rule.

In this example, we are performing an upper tailed test (H 1 : μ> 191), with a Z test statistic and selected α =0.05. Reject H 0 if Z > 1.645.

We now substitute the sample data into the formula for the test statistic identified in Step 2.

We reject H 0 because 2.38 > 1.645. We have statistically significant evidence at a =0.05, to show that the mean weight in men in 2006 is more than 191 pounds. Because we rejected the null hypothesis, we now approximate the p-value which is the likelihood of observing the sample data if the null hypothesis is true. An alternative definition of the p-value is the smallest level of significance where we can still reject H 0 . In this example, we observed Z=2.38 and for α=0.05, the critical value was 1.645. Because 2.38 exceeded 1.645 we rejected H 0 . In our conclusion we reported a statistically significant increase in mean weight at a 5% level of significance. Using the table of critical values for upper tailed tests, we can approximate the p-value. If we select α=0.025, the critical value is 1.96, and we still reject H 0 because 2.38 > 1.960. If we select α=0.010 the critical value is 2.326, and we still reject H 0 because 2.38 > 2.326. However, if we select α=0.005, the critical value is 2.576, and we cannot reject H 0 because 2.38 < 2.576. Therefore, the smallest α where we still reject H 0 is 0.010. This is the p-value. A statistical computing package would produce a more precise p-value which would be in between 0.005 and 0.010. Here we are approximating the p-value and would report p < 0.010.

In all tests of hypothesis, there are two types of errors that can be committed. The first is called a Type I error and refers to the situation where we incorrectly reject H 0 when in fact it is true. This is also called a false positive result (as we incorrectly conclude that the research hypothesis is true when in fact it is not). When we run a test of hypothesis and decide to reject H 0 (e.g., because the test statistic exceeds the critical value in an upper tailed test) then either we make a correct decision because the research hypothesis is true or we commit a Type I error. The different conclusions are summarized in the table below. Note that we will never know whether the null hypothesis is really true or false (i.e., we will never know which row of the following table reflects reality).

Table - Conclusions in Test of Hypothesis


is True	Correct Decision	Type I Error
is False	Type II Error	Correct Decision

In the first step of the hypothesis test, we select a level of significance, α, and α= P(Type I error). Because we purposely select a small value for α, we control the probability of committing a Type I error. For example, if we select α=0.05, and our test tells us to reject H 0 , then there is a 5% probability that we commit a Type I error. Most investigators are very comfortable with this and are confident when rejecting H 0 that the research hypothesis is true (as it is the more likely scenario when we reject H 0 ).

When we run a test of hypothesis and decide not to reject H 0 (e.g., because the test statistic is below the critical value in an upper tailed test) then either we make a correct decision because the null hypothesis is true or we commit a Type II error. Beta (β) represents the probability of a Type II error and is defined as follows: β=P(Type II error) = P(Do not Reject H 0 | H 0 is false). Unfortunately, we cannot choose β to be small (e.g., 0.05) to control the probability of committing a Type II error because β depends on several factors including the sample size, α, and the research hypothesis. When we do not reject H 0 , it may be very likely that we are committing a Type II error (i.e., failing to reject H 0 when in fact it is false). Therefore, when tests are run and the null hypothesis is not rejected we often make a weak concluding statement allowing for the possibility that we might be committing a Type II error. If we do not reject H 0 , we conclude that we do not have significant evidence to show that H 1 is true. We do not conclude that H 0 is true.

The most common reason for a Type II error is a small sample size.

return to top | previous page | next page

What 'Fail to Reject' Means in a Hypothesis Test

Casarsa Guru/Getty Images

Inferential Statistics
Statistics Tutorials
Probability & Games
Descriptive Statistics
Applications Of Statistics
Math Tutorials
Pre Algebra & Algebra
Exponential Decay
Worksheets By Grade
Ph.D., Mathematics, Purdue University
M.S., Mathematics, Purdue University
B.A., Mathematics, Physics, and Chemistry, Anderson University

In statistics , scientists can perform a number of different significance tests to determine if there is a relationship between two phenomena. One of the first they usually perform is a null hypothesis test. In short, the null hypothesis states that there is no meaningful relationship between two measured phenomena. After a performing a test, scientists can:

Reject the null hypothesis (meaning there is a definite, consequential relationship between the two phenomena), or
Fail to reject the null hypothesis (meaning the test has not identified a consequential relationship between the two phenomena)

Key Takeaways: The Null Hypothesis

• In a test of significance, the null hypothesis states that there is no meaningful relationship between two measured phenomena.

• By comparing the null hypothesis to an alternative hypothesis, scientists can either reject or fail to reject the null hypothesis.

• The null hypothesis cannot be positively proven. Rather, all that scientists can determine from a test of significance is that the evidence collected does or does not disprove the null hypothesis.

It is important to note that a failure to reject does not mean that the null hypothesis is true—only that the test did not prove it to be false. In some cases, depending on the experiment, a relationship may exist between two phenomena that is not identified by the experiment. In such cases, new experiments must be designed to rule out alternative hypotheses.

Null vs. Alternative Hypothesis

The null hypothesis is considered the default in a scientific experiment . In contrast, an alternative hypothesis is one that claims that there is a meaningful relationship between two phenomena. These two competing hypotheses can be compared by performing a statistical hypothesis test, which determines whether there is a statistically significant relationship between the data.

For example, scientists studying the water quality of a stream may wish to determine whether a certain chemical affects the acidity of the water. The null hypothesis—that the chemical has no effect on the water quality—can be tested by measuring the pH level of two water samples, one of which contains some of the chemical and one of which has been left untouched. If the sample with the added chemical is measurably more or less acidic—as determined through statistical analysis—it is a reason to reject the null hypothesis. If the sample's acidity is unchanged, it is a reason to not reject the null hypothesis.

When scientists design experiments, they attempt to find evidence for the alternative hypothesis. They do not try to prove that the null hypothesis is true. The null hypothesis is assumed to be an accurate statement until contrary evidence proves otherwise. As a result, a test of significance does not produce any evidence pertaining to the truth of the null hypothesis.

Failing to Reject vs. Accept

In an experiment, the null hypothesis and the alternative hypothesis should be carefully formulated such that one and only one of these statements is true. If the collected data supports the alternative hypothesis, then the null hypothesis can be rejected as false. However, if the data does not support the alternative hypothesis, this does not mean that the null hypothesis is true. All it means is that the null hypothesis has not been disproven—hence the term "failure to reject." A "failure to reject" a hypothesis should not be confused with acceptance.

In mathematics, negations are typically formed by simply placing the word “not” in the correct place. Using this convention, tests of significance allow scientists to either reject or not reject the null hypothesis. It sometimes takes a moment to realize that “not rejecting” is not the same as "accepting."

Null Hypothesis Example

In many ways, the philosophy behind a test of significance is similar to that of a trial. At the beginning of the proceedings, when the defendant enters a plea of “not guilty,” it is analogous to the statement of the null hypothesis. While the defendant may indeed be innocent, there is no plea of “innocent” to be formally made in court. The alternative hypothesis of “guilty” is what the prosecutor attempts to demonstrate.

The presumption at the outset of the trial is that the defendant is innocent. In theory, there is no need for the defendant to prove that he or she is innocent. The burden of proof is on the prosecuting attorney, who must marshal enough evidence to convince the jury that the defendant is guilty beyond a reasonable doubt. Likewise, in a test of significance, a scientist can only reject the null hypothesis by providing evidence for the alternative hypothesis.

If there is not enough evidence in a trial to demonstrate guilt, then the defendant is declared “not guilty.” This claim has nothing to do with innocence; it merely reflects the fact that the prosecution failed to provide enough evidence of guilt. In a similar way, a failure to reject the null hypothesis in a significance test does not mean that the null hypothesis is true. It only means that the scientist was unable to provide enough evidence for the alternative hypothesis.

For example, scientists testing the effects of a certain pesticide on crop yields might design an experiment in which some crops are left untreated and others are treated with varying amounts of pesticide. Any result in which the crop yields varied based on pesticide exposure—assuming all other variables are equal—would provide strong evidence for the alternative hypothesis (that the pesticide does affect crop yields). As a result, the scientists would have reason to reject the null hypothesis.

Type I and Type II Errors in Statistics
Null Hypothesis and Alternative Hypothesis
An Example of Chi-Square Test for a Multinomial Experiment
The Difference Between Type I and Type II Errors in Hypothesis Testing
What Level of Alpha Determines Statistical Significance?
What Is the Difference Between Alpha and P-Values?
How to Find Critical Values with a Chi-Square Table
The Runs Test for Random Sequences
An Example of a Hypothesis Test
What Is ANOVA?
Example of a Permutation Test
Degrees of Freedom for Independence of Variables in Two-Way Table
How to Find Degrees of Freedom in Statistics
Example of an ANOVA Calculation
Confidence Intervals: 4 Common Mistakes
How to Construct a Confidence Interval for a Population Proportion

Optimal Tests of the Composite Null Hypothesis Arising in Mediation Analysis

The indirect effect of an exposure on an outcome through an intermediate variable can be identified by a product of regression coefficients under certain causal and regression modeling assumptions. In this context, the null hypothesis of no indirect effect is a composite null hypothesis, as the null holds if either regression coefficient is zero. A consequence is that traditional hypothesis tests are severely underpowered near the origin (i.e., when both coefficients are small with respect to standard errors). We propose hypothesis tests that (i) preserve level alpha type 1 error, (ii) meaningfully improve power when both true underlying effects are small relative to sample size, and (iii) preserve power when at least one is not. One approach gives a closed-form test that is minimax optimal with respect to local power over the alternative parameter space. Another uses sparse linear programming to produce an approximately optimal test for a Bayes risk criterion. We discuss adaptations for performing large-scale hypothesis testing as well as modifications that yield improved interpretability. We provide an R package that implements the minimax optimal test.

Keywords: Bayes risk optimality, Causal inference, Large-scale hypothesis testing, Non-uniform asymptotics, Similar test

1 INTRODUCTION

Mediation analysis is a widely popular discipline that seeks to understand the mechanism by which an exposure affects an outcome by learning about intermediate events that transmit part or all of its effect. For instance, if one is interested in the effect of an exposure A 𝐴 A italic_A on an outcome Y 𝑌 Y italic_Y , one might posit that at least in part, A 𝐴 A italic_A affects Y 𝑌 Y italic_Y by first affecting some intermediate event M 𝑀 M italic_M , which in turn affects Y 𝑌 Y italic_Y . The effect along such a causal pathway is known as an indirect effect. Despite its long history and broad application, with an exception from recent work ( van Garderen and van Giersbergen, 2022a, ) , existing hypothesis tests of a single mediated effect are overly conservative and underpowered in a certain region of the alternative hypothesis space. In this article, we demonstrate the reason for this suboptimal behavior, and develop new hypothesis tests that deliver optimal power in some decision theoretic senses while preserving type 1 error uniformly over the composite null subspace of the parameter space. We focus on the case in which the indirect effect is identified by a product of coefficients or functions of coefficients that can be estimated with uniform joint convergence to a bivariate normal distribution with diagonal covariance matrix. In fact, our approach is not limited to the realm of mediation analysis, but can be applied to test for any product of two coefficients that are estimable in the above sense.

Briefly, the inferential problem that arises in mediation analysis is that when the mediated effect is identified by a product of coefficients, even while the joint distribution of estimators of these coefficients may converge uniformly to a bivariate normal distribution, neither their product nor the minimum of their absolute values will converge uniformly to a Gaussian law. Thus, asymptotic approximation-based univariate test statistics that are a function of either of these summaries of the two coefficient estimates will have poor properties in an important region of the parameter space for any given finite sample.

Previously, MacKinnon et al., ( 2002 ) and Barfield et al., ( 2017 ) presented results from simulation studies comparing hypothesis tests of a mediated effect. Both articles observed that all existing tests are either underpowered in some scenarios or do not preserve nominal type 1 error in all scenarios. Both articles found the so-called joint significance test to be the best overall performing test, while Barfield et al., ( 2017 ) found a bootstrap-based test to have comparable performance across some scenarios, with the exception of the setting with a rare binary outcome. Huang, ( 2019 ) proved that the joint significance test yields a smaller p 𝑝 p italic_p -value than those of both normality-based tests and normal product-based tests.

Barfield et al., ( 2017 ) highlighted the problem of large-scale hypothesis testing for mediated effects, which has become a popular inferential task in genomics, where genomic measures such as gene expression or DNA methylation are hypothesized to be potential mediators of the effect of genes or other exposures on various outcomes. In fact, the conservative behavior of mediation hypothesis tests are most evident in large-scale hypothesis tests, since one can then compare the distribution of p 𝑝 p italic_p -values with the uniform distribution. Huang, ( 2019 ) showed that the joint significance test and delta method-based tests both generate p 𝑝 p italic_p -values forming a distribution that stochastically dominates the uniform distribution. However, while this behavior is readily observable in large-scale hypothesis tests, the problem is no different for a single hypothesis test; it is merely less obvious.

Recently, Huang, ( 2019 ) , Dai et al., ( 2020 ) , Liu et al., ( 2022 ) , and Du et al., ( 2023 ) developed large-scale hypothesis testing procedures for mediated effects that account for the conservativeness of standard tests. The latter compared these methods as well as traditional methods in a large simulation study. The method proposed by Huang, ( 2019 ) is based on a distributional assumption about the two coefficients among all distributions being tested that satisfy the null hypothesis. By contrast, the methods proposed by Dai et al., ( 2020 ) , Liu et al., ( 2022 ) , and Du et al., ( 2023 ) involve estimating the proportions of three different components of the composite null hypothesis: when both coefficients are zero, when one is zero and the other is not, and vice versa. Dai et al., ( 2020 ) and Du et al., ( 2023 ) then relaxed the threshold of the joint significance test and delta method-based test, respectively, based on these estimated proportions. Liu et al., ( 2022 ) used the estimated proportions to construct a new test statistic based on p 𝑝 p italic_p -values attained under each of these components of the null hypothesis. Our proposed methods resolve the conservativeness issue across the entire null hypothesis space even for a single test, hence they require neither assumptions about the distributions of the coefficients nor estimation of proportions of components of the null hypothesis space. The latter is important, because in finite samples, there is no single distribution of a test statistic under the sub-case of the null hypothesis in which one parameter is null and the other is not. The distribution of a test statistic in this sub-case can vary from being well-approximated by the distribution when one parameter is zero and the other is infinite to being well-approximated by the distribution when both parameters are zero (indeed, this sub-case contains parameter values arbitrarily close to (0,0)). Instead, we can simply extend our method to the large-scale hypothesis test setting while adjusting for multiple testing using standard Bonferroni or Benjamini–Hochberg corrections.

van Garderen and van Giersbergen, 2022a is the most closely related work to this article. The authors develop a test for a mediated effect based on defining a rejection region in ℝ 2 superscript ℝ 2 \mathbb{R}^{2} blackboard_R start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT . In their original version (van Garderen and van Giersbergen,, 2020 ) , they prove that a similar test does not exist within a certain class of tests. In this article, we show that a similar test does in fact exist in a slightly expanded class of tests, and that it is the unique such test in this class (in a more recent version ( van Garderen and van Giersbergen, 2022a, ) , the authors now recognize the existence of this test). They focus on developing an almost-similar test, i.e., they attempt to get as close to a similar test as possible while preserving type 1 error by optimizing a particular objective function involving a penalty for deviations from the nominal type 1 error level. By contrast, we consider two approaches for optimizing decision theoretic criteria that characterize power while preserving type 1 error. The solution to one of these has a closed form and is an exactly similar test. The other is an approximate Bayes risk optimal test inspired by the test of Rosenblum et al., ( 2014 ) .

The remainder of the article is organized as follows. In Section 2 , we formalize the problem and explain the shortcomings of traditional tests. In Sections 3 and 4 , we present the minimax optimal and Bayes risk optimal test, respectively. In Section 5 , we discuss adaptations for large-scale mediation hypothesis testing. In Section 6 , we discuss interpretability challenges with the proposed tests, and introduce modifications leading to improved interpretability. In Section 7 , we present results from simulation studies. In Section 8 , we apply our methodology to two data sets: one to test whether cognition mediates the effect of cognitive remediation therapy on selt-esteem in patients with schizophrenia, and another to test many mediation hypotheses of whether a host of DNA methylation CpG sites mediate the effect of smoking status on lung function. In Section 9 , we conclude with a discussion.

2 PRELIMINARIES

We begin with the general problem statement, which we will then connect to mediation analysis. Suppose we have n 𝑛 n italic_n independent, identically distributed (i.i.d.) observations from a distribution P 𝜹 subscript 𝑃 𝜹 P_{\bm{\delta}} italic_P start_POSTSUBSCRIPT bold_italic_δ end_POSTSUBSCRIPT indexed by the parameter 𝜹 𝜹 \bm{\delta} bold_italic_δ , which contains two scalar parameters δ x subscript 𝛿 𝑥 \delta_{x} italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT and δ y subscript 𝛿 𝑦 \delta_{y} italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT , and we wish to test the null hypothesis H 0 : ` ⁢ ` ⁢ δ x ⁢ δ y = 0 ⁢ " : subscript 𝐻 0 ` ` subscript 𝛿 𝑥 subscript 𝛿 𝑦 0 " H_{0}:``\delta_{x}\delta_{y}=0" italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT : ` ` italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT = 0 " against its alternative H 1 : ` ⁢ ` ⁢ δ x ⁢ δ y ≠ 0 ⁢ " : subscript 𝐻 1 ` ` subscript 𝛿 𝑥 subscript 𝛿 𝑦 0 " H_{1}:``\delta_{x}\delta_{y}\neq 0" italic_H start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT : ` ` italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT ≠ 0 " . Further, suppose we have a uniformly asymptotically normal and unbiased estimator (Robins and Ritov,, 1997 ) ( δ ^ x , δ ^ y ) subscript ^ 𝛿 𝑥 subscript ^ 𝛿 𝑦 (\hat{\delta}_{x},\hat{\delta}_{y}) ( over^ start_ARG italic_δ end_ARG start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT , over^ start_ARG italic_δ end_ARG start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT ) for ( δ x , δ y ) subscript 𝛿 𝑥 subscript 𝛿 𝑦 (\delta_{x},\delta_{y}) ( italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT , italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT ) , i.e.,

(1)

as n → ∞ → 𝑛 n\rightarrow\infty italic_n → ∞ for all ( t x , t y ) ⊤ ∈ ℝ 2 superscript subscript 𝑡 𝑥 subscript 𝑡 𝑦 top superscript ℝ 2 (t_{x},t_{y})^{\top}\in\mathbb{R}^{2} ( italic_t start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT , italic_t start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT ) start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT ∈ blackboard_R start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT , where 𝚺 𝒏 subscript 𝚺 𝒏 \bm{\Sigma_{n}} bold_Σ start_POSTSUBSCRIPT bold_italic_n end_POSTSUBSCRIPT is a diagonal matrix that is a consistent estimator of the asymptotic covariance matrix, and Φ 2 subscript Φ 2 \Phi_{2} roman_Φ start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT is the cumulative distribution function of the bivariate Gaussian distribution with identity covariance. We wish to test H 0 subscript 𝐻 0 H_{0} italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT against H 1 subscript 𝐻 1 H_{1} italic_H start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT with at most α 𝛼 \alpha italic_α type 1 error for each ( δ x , δ y ) subscript 𝛿 𝑥 subscript 𝛿 𝑦 (\delta_{x},\delta_{y}) ( italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT , italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT ) satisfying δ x ⁢ δ y = 0 subscript 𝛿 𝑥 subscript 𝛿 𝑦 0 \delta_{x}\delta_{y}=0 italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT = 0 and maximizing power (in some sense) everywhere else. Clearly, H 0 subscript 𝐻 0 H_{0} italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT is a very particular type of composite null hypothesis, which in the space spanned by δ x subscript 𝛿 𝑥 \delta_{x} italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT and δ y subscript 𝛿 𝑦 \delta_{y} italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT consists of the x 𝑥 x italic_x and y 𝑦 y italic_y axes.

The composite null hypothesis H 0 subscript 𝐻 0 H_{0} italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT arises naturally in mediation analysis under certain modeling assumptions. Suppose we observe n 𝑛 n italic_n i.i.d. copies of ( 𝑪 ⊤ , A , M , Y ) ⊤ superscript superscript 𝑪 top 𝐴 𝑀 𝑌 top (\bm{C}^{\top},A,M,Y)^{\top} ( bold_italic_C start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT , italic_A , italic_M , italic_Y ) start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT , where A 𝐴 A italic_A is the exposure of interest, Y 𝑌 Y italic_Y is the outcome of interest, M 𝑀 M italic_M is a potential mediator that is temporally intermediate to A 𝐴 A italic_A and Y 𝑌 Y italic_Y , and 𝑪 𝑪 \bm{C} bold_italic_C is a vector of baseline covariates that we will assume throughout to be sufficient to control for various sorts of confounding needed for the indirect effect to be identified. The natural indirect effect (NIE) is the mediated effect of A 𝐴 A italic_A on Y 𝑌 Y italic_Y through M 𝑀 M italic_M . We formally define the NIE and discuss its identification in the Supplementary Materials. If the linear models with main effect terms given by

				(2)
				(3)

(4)

superscript subscript ^ 𝛿 𝑦 2 superscript subscript 𝑠 𝑥 2 superscript subscript ^ 𝛿 𝑥 2 superscript subscript 𝑠 𝑦 2 1 2 ↝ 𝒩 0 1 Z_{n}^{\text{prod}}:=n^{1/2}\hat{\delta}_{x}\hat{\delta}_{y}/(\hat{\delta}_{y}% ^{2}s_{x}^{2}+\hat{\delta}_{x}^{2}s_{y}^{2})^{1/2}\rightsquigarrow\mathcal{N}(% 0,1) italic_Z start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT start_POSTSUPERSCRIPT prod end_POSTSUPERSCRIPT := italic_n start_POSTSUPERSCRIPT 1 / 2 end_POSTSUPERSCRIPT over^ start_ARG italic_δ end_ARG start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT over^ start_ARG italic_δ end_ARG start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT / ( over^ start_ARG italic_δ end_ARG start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT italic_s start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT + over^ start_ARG italic_δ end_ARG start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT italic_s start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT ) start_POSTSUPERSCRIPT 1 / 2 end_POSTSUPERSCRIPT ↝ caligraphic_N ( 0 , 1 ) , where s x 2 subscript superscript 𝑠 2 𝑥 s^{2}_{x} italic_s start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT and s y 2 subscript superscript 𝑠 2 𝑦 s^{2}_{y} italic_s start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT are consistent estimates of σ x 2 subscript superscript 𝜎 2 𝑥 \sigma^{2}_{x} italic_σ start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT and σ y 2 subscript superscript 𝜎 2 𝑦 \sigma^{2}_{y} italic_σ start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT , respectively. However, as ( δ x , δ y ) → ( 0 , 0 ) → subscript 𝛿 𝑥 subscript 𝛿 𝑦 0 0 (\delta_{x},\delta_{y})\rightarrow(0,0) ( italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT , italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT ) → ( 0 , 0 ) , this no longer holds, as the denominator is also converging to zero. Liu et al., ( 2022 ) showed that this instead converges to a centered normal distribution with variance 1/4. Thus, the convergence in distribution of the delta method test statistic Z n prod superscript subscript 𝑍 𝑛 prod Z_{n}^{\text{prod}} italic_Z start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT start_POSTSUPERSCRIPT prod end_POSTSUPERSCRIPT is not uniform, because for any given sample size, no matter how large, there will be a region in the parameter space around ( 0 , 0 ) 0 0 (0,0) ( 0 , 0 ) where the standard normal approximation can be very poor. This is especially problematic, as the region around ( 0 , 0 ) 0 0 (0,0) ( 0 , 0 ) is precisely where we would expect the truth to often lie. As one moves closer to the origin in the parameter space, the true distribution of Z n prod superscript subscript 𝑍 𝑛 prod Z_{n}^{\text{prod}} italic_Z start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT start_POSTSUPERSCRIPT prod end_POSTSUPERSCRIPT begins to more closely resemble N ⁢ ( 0 , 1 / 4 ) 𝑁 0 1 4 N(0,1/4) italic_N ( 0 , 1 / 4 ) . This is demonstrated by a Monte Carlo sampling approximation of density functions in Figure S1.a in the Supplementary Materials, where we fix δ y = 0 subscript 𝛿 𝑦 0 \delta_{y}=0 italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT = 0 and vary δ x subscript 𝛿 𝑥 \delta_{x} italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT from 0 to 0.3. The delta method is using an approximation based on the standard normal distribution, when in reality, the test statistic’s true distribution is much more concentrated about zero, as can be seen in the figure. This explains the conservative behavior of the delta method-based test near the origin.

Hypothesis tests based on inverting bootstrap confidence intervals are also known to perform poorly near the origin of the parameter space. The reason is that bootstrap theory requires continuity in the asymptotic distribution over the parameter space. As we have seen, there is a singularity in the pointwise asymptotic distribution at the origin.

Another popular test of the composite null H 0 subscript 𝐻 0 H_{0} italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT against its alternative H 1 subscript 𝐻 1 H_{1} italic_H start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT is known as the joint significance test (Cohen et al.,, 2013 ) , which is an intersection-union test based on the simple logic that both δ x subscript 𝛿 𝑥 \delta_{x} italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT and δ y subscript 𝛿 𝑦 \delta_{y} italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT must be nonzero for δ x ⁢ δ y subscript 𝛿 𝑥 subscript 𝛿 𝑦 \delta_{x}\delta_{y} italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT to be nonzero. The joint significance test with nominal level α 𝛼 \alpha italic_α amounts to testing the two null hypotheses H 0 x : ` ⁢ ` ⁢ δ x = 0 ⁢ " : superscript subscript 𝐻 0 𝑥 ` ` subscript 𝛿 𝑥 0 " H_{0}^{x}:``\delta_{x}=0" italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT : ` ` italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT = 0 " and H 0 y : ` ⁢ ` ⁢ δ y = 0 ⁢ " : superscript subscript 𝐻 0 𝑦 ` ` subscript 𝛿 𝑦 0 " H_{0}^{y}:``\delta_{y}=0" italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT : ` ` italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT = 0 " against their alternatives H 1 x : ` ⁢ ` ⁢ δ x ≠ 0 ⁢ " : superscript subscript 𝐻 1 𝑥 ` ` subscript 𝛿 𝑥 0 " H_{1}^{x}:``\delta_{x}\neq 0" italic_H start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT : ` ` italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT ≠ 0 " and H 1 y : ` ⁢ ` ⁢ δ y ≠ 0 ⁢ " : superscript subscript 𝐻 1 𝑦 ` ` subscript 𝛿 𝑦 0 " H_{1}^{y}:``\delta_{y}\neq 0" italic_H start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT : ` ` italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT ≠ 0 " separately using the Wald statistics Z n x := n ⁢ δ ^ x / s x assign subscript superscript 𝑍 𝑥 𝑛 𝑛 subscript ^ 𝛿 𝑥 subscript 𝑠 𝑥 Z^{x}_{n}:=\sqrt{n}\hat{\delta}_{x}/s_{x} italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT := square-root start_ARG italic_n end_ARG over^ start_ARG italic_δ end_ARG start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT / italic_s start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT and Z n y := n ⁢ δ ^ y / s y assign subscript superscript 𝑍 𝑦 𝑛 𝑛 subscript ^ 𝛿 𝑦 subscript 𝑠 𝑦 Z^{y}_{n}:=\sqrt{n}\hat{\delta}_{y}/s_{y} italic_Z start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT := square-root start_ARG italic_n end_ARG over^ start_ARG italic_δ end_ARG start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT / italic_s start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT , and rejecting H 0 subscript 𝐻 0 H_{0} italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT for H 1 subscript 𝐻 1 H_{1} italic_H start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT only if H 0 x superscript subscript 𝐻 0 𝑥 H_{0}^{x} italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT and H 0 y superscript subscript 𝐻 0 𝑦 H_{0}^{y} italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT are both rejected for their alternatives by the corresponding Wald tests with nominal level α 𝛼 \alpha italic_α . As we previously noted, this test has been shown to perform better in simulations than other common tests of H 0 subscript 𝐻 0 H_{0} italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT against H 1 subscript 𝐻 1 H_{1} italic_H start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT . However, it still suffers from the lack of power near the origin of the parameter space we see in other tests. This is once again due to a lack of uniform convergence near the origin. The joint significance test implicitly relies on the approximation Z n min := | Z n x | ∧ | Z n y | ∼ | 𝒩 | ⁢ ( 0 , 1 ) assign superscript subscript 𝑍 𝑛 min superscript subscript 𝑍 𝑛 𝑥 superscript subscript 𝑍 𝑛 𝑦 similar-to 𝒩 0 1 Z_{n}^{\text{min}}:=|Z_{n}^{x}|\wedge|Z_{n}^{y}|\sim|\mathcal{N}|(0,1) italic_Z start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT start_POSTSUPERSCRIPT min end_POSTSUPERSCRIPT := | italic_Z start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT | ∧ | italic_Z start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT | ∼ | caligraphic_N | ( 0 , 1 ) , where | 𝒩 | ⁢ ( 0 , 1 ) 𝒩 0 1 |\mathcal{N}|(0,1) | caligraphic_N | ( 0 , 1 ) represents the folded normal distribution with mean zero and variance one. However, this approximation is poor when δ x subscript 𝛿 𝑥 \delta_{x} italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT and δ y subscript 𝛿 𝑦 \delta_{y} italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT are both close to zero, as is shown in Figure S1.b in the Supplementary Materials, where we once again fix δ y = 0 subscript 𝛿 𝑦 0 \delta_{y}=0 italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT = 0 and vary δ x subscript 𝛿 𝑥 \delta_{x} italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT from 0 to 0.3.

In order to avoid the problems that arise due to non-uniform convergence, we will instead focus on constructing a rejection region in the parameter space spanned by the vector ( δ x , δ y ) subscript 𝛿 𝑥 subscript 𝛿 𝑦 (\delta_{x},\delta_{y}) ( italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT , italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT ) in ℝ 2 superscript ℝ 2 \mathbb{R}^{2} blackboard_R start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT , rather than the parameter space spanned by the product δ x ⁢ δ y subscript 𝛿 𝑥 subscript 𝛿 𝑦 \delta_{x}\delta_{y} italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT in ℝ ℝ \mathbb{R} blackboard_R . In the former, we know convergence is uniform and there are no discontinuities in the asymptotic distribution over the parameter space. Studying the rejection regions of the traditional tests in ℝ 2 superscript ℝ 2 \mathbb{R}^{2} blackboard_R start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT illustrates their conservative behavior from another perspective.


(a)		(b)

Because we are taking the intersection of rejection regions of two size- α 𝛼 \alpha italic_α tests, the resulting test must necessarily be conservative. In fact, when ( δ x ∗ , δ y ∗ ) = ( 0 , 0 ) superscript subscript 𝛿 𝑥 superscript subscript 𝛿 𝑦 0 0 (\delta_{x}^{*},\delta_{y}^{*})=(0,0) ( italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT , italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT ) = ( 0 , 0 ) , the probability of being in the joint significance test rejection region is α 2 superscript 𝛼 2 \alpha^{2} italic_α start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT , well below the desired level α 𝛼 \alpha italic_α . By the continuity of the rejection probability in ( δ x ∗ , δ y ∗ ) superscript subscript 𝛿 𝑥 superscript subscript 𝛿 𝑦 (\delta_{x}^{*},\delta_{y}^{*}) ( italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT , italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT ) , the rejection probability is likewise well below α 𝛼 \alpha italic_α in a region around the origin, hence the underpoweredness of the joint significance test. That is, the worst-case type 2 error of the joint significance test is

The rejection region corresponding to the delta method-based test has been shown to be contained in that of the joint significance test (Huang,, 2019 ; van Garderen and van Giersbergen, 2022a, ) , and therefore the delta method-based test is uniformly more conservative than the joint significance test, hence it suffers from the same problem.

Our goal in the following two sections is to define a new test by constructing a rejection region that preserves type 1 error uniformly over the null hypothesis space, but improves power in the alternative hypothesis space, particularly in the region around the origin of the parameter space.

3 MINIMAX OPTIMAL TEST

(5)

In words, the rejection region R ∗ superscript 𝑅 R^{*} italic_R start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT generates a test with type 1 error α 𝛼 \alpha italic_α that achieves the minimax risk of the 0-1 loss function, i.e., that yields the largest worst-case power. By continuity of the power function in ( δ x ∗ , δ y ∗ ) subscript superscript 𝛿 𝑥 subscript superscript 𝛿 𝑦 (\delta^{*}_{x},\delta^{*}_{y}) ( italic_δ start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT , italic_δ start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT ) , the minimax optimal power is upper bounded by α 𝛼 \alpha italic_α , since the rejection probability can be at most α 𝛼 \alpha italic_α at any given value of ( δ x ∗ , δ y ∗ ) subscript superscript 𝛿 𝑥 subscript superscript 𝛿 𝑦 (\delta^{*}_{x},\delta^{*}_{y}) ( italic_δ start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT , italic_δ start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT ) in the null hypothesis space, and can be arbitrarily close to this rejection probability in a small enough neighborhood around that point, which will contain elements of the alternative hypothesis space. Moreover, if ( 5 ) is attainable, a minimax optimal test generated by the rejection region R 𝑅 R italic_R must satisfy

(6)

A test satisfying ( 6 ) is known as a similar test (Lehmann et al.,, 2005 ) . Similarity is an important property that is closely tied to uniformly most powerful unbiased tests in the classical hypothesis testing literature (e.g., see Chapter 4 of Lehmann et al., ( 2005 ) ). In our case, it is important because a non-similar test must have type 1 error either greater than or less than α 𝛼 \alpha italic_α somewhere in the null hypothesis space. In the former case, the test will fail to preserve type 1 error. In the latter, by continuity of the rejection probability as a function of the true parameter, the rejection probability will necessarily be less than α 𝛼 \alpha italic_α in some neighborhood that also contains the alternative hypothesis space. Thus, a non-similar test will necessarily be a biased test and underpowered in a region of the alternative hypothesis space.

3.1 A Minimax Optimal and Similar Test for Unit Fraction α 𝛼 \alpha italic_α

Theorem 1 ..

The rejection region R m ⁢ m subscript 𝑅 𝑚 𝑚 R_{mm} italic_R start_POSTSUBSCRIPT italic_m italic_m end_POSTSUBSCRIPT satisfies ( 6 ) and generates a similar test.

All proofs are presented in the appendix. The essence of the proof of Theorem 1 is that when δ y ∗ = 0 subscript superscript 𝛿 𝑦 0 \delta^{*}_{y}=0 italic_δ start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT = 0 , whatever level Z ∗ x subscript superscript 𝑍 𝑥 Z^{x}_{*} italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT takes, the conditional probability of Z ∗ y subscript superscript 𝑍 𝑦 Z^{y}_{*} italic_Z start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT being in R m ⁢ m subscript 𝑅 𝑚 𝑚 R_{mm} italic_R start_POSTSUBSCRIPT italic_m italic_m end_POSTSUBSCRIPT given Z ∗ x subscript superscript 𝑍 𝑥 Z^{x}_{*} italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT equals α 𝛼 \alpha italic_α , since the probability of being in each vertical interval is α / 2 𝛼 2 \alpha/2 italic_α / 2 for a standard normal distribution. The same holds for Z ∗ x subscript superscript 𝑍 𝑥 Z^{x}_{*} italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT when δ x ∗ = 0 subscript superscript 𝛿 𝑥 0 \delta^{*}_{x}=0 italic_δ start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT = 0 by symmetry.

Corollary 1 .

van Garderen and van Giersbergen, ( 2020 ) give a result stating that there is no similar test of H 0 subscript 𝐻 0 H_{0} italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT against H 1 subscript 𝐻 1 H_{1} italic_H start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT within a particular class of tests defined by a rejection region generated by rotating and reflecting a monotonically increasing function from zero to infinity. While Corollary 1 may appear to contradict this result, R m ⁢ m subscript 𝑅 𝑚 𝑚 R_{mm} italic_R start_POSTSUBSCRIPT italic_m italic_m end_POSTSUBSCRIPT does not in fact belong to the class considered by van Garderen and van Giersbergen, ( 2020 ) , but rather belongs to a class that relaxes the restriction that the function must be monotonically increasing to allow for it to be monotonically nondecreasing (though the more recent version ( van Garderen and van Giersbergen, 2022a, ) recognizes the existence of this function). In fact, the following theorem states that the test generated by R m ⁢ m subscript 𝑅 𝑚 𝑚 R_{mm} italic_R start_POSTSUBSCRIPT italic_m italic_m end_POSTSUBSCRIPT is the only similar test in this relaxed class up to a set of measure zero.

Theorem 2 .

Let ℱ ℱ \mathcal{F} caligraphic_F be the class of all monotonically nondecreasing functions mapping all x 𝑥 x italic_x from the nonnegative real numbers to [ 0 , x ] 0 𝑥 [0,x] [ 0 , italic_x ] , and for any f ∈ ℱ 𝑓 ℱ f\in\mathcal{F} italic_f ∈ caligraphic_F , let R f subscript 𝑅 𝑓 R_{f} italic_R start_POSTSUBSCRIPT italic_f end_POSTSUBSCRIPT be the region generated by taking all possible negations and permutations of the region { ( x , y ) : y ∈ ( f ⁢ ( x ) , x ] } conditional-set 𝑥 𝑦 𝑦 𝑓 𝑥 𝑥 \{(x,y):y\in(f(x),x]\} { ( italic_x , italic_y ) : italic_y ∈ ( italic_f ( italic_x ) , italic_x ] } , or equivalently reflecting this region about the x 𝑥 x italic_x , y 𝑦 y italic_y , y = x 𝑦 𝑥 y=x italic_y = italic_x , and y = − x 𝑦 𝑥 y=-x italic_y = - italic_x axes, and rotating it π / 2 𝜋 2 \pi/2 italic_π / 2 , π 𝜋 \pi italic_π , and 3 ⁢ π / 2 3 𝜋 2 3\pi/2 3 italic_π / 2 radians about the origin. The function f m ⁢ m ⁢ ( x ) := ∑ k = 1 / α 2 / α a k − 1 ⁢ I ⁢ ( a k − 1 ≤ x < a k ) assign subscript 𝑓 𝑚 𝑚 𝑥 superscript subscript 𝑘 1 𝛼 2 𝛼 subscript 𝑎 𝑘 1 𝐼 subscript 𝑎 𝑘 1 𝑥 subscript 𝑎 𝑘 f_{mm}(x):=\sum_{k=1/\alpha}^{2/\alpha}a_{k-1}I(a_{k-1}\leq x<a_{k}) italic_f start_POSTSUBSCRIPT italic_m italic_m end_POSTSUBSCRIPT ( italic_x ) := ∑ start_POSTSUBSCRIPT italic_k = 1 / italic_α end_POSTSUBSCRIPT start_POSTSUPERSCRIPT 2 / italic_α end_POSTSUPERSCRIPT italic_a start_POSTSUBSCRIPT italic_k - 1 end_POSTSUBSCRIPT italic_I ( italic_a start_POSTSUBSCRIPT italic_k - 1 end_POSTSUBSCRIPT ≤ italic_x < italic_a start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ) , which generates R m ⁢ m subscript 𝑅 𝑚 𝑚 R_{mm} italic_R start_POSTSUBSCRIPT italic_m italic_m end_POSTSUBSCRIPT , is the unique function in ℱ ℱ \mathcal{F} caligraphic_F (up to a set of measure zero) that generates a similar test.

In addition to minimax optimality, this test has some other desirable properties. It has a simple, exact closed form, making it very fast and straightforward to implement. Additionally, it is nonrandom, and is symmetric with respect to negation and permutations. One less desirable property is that the test will reject for ( Z n x , Z n y ) subscript superscript 𝑍 𝑥 𝑛 subscript superscript 𝑍 𝑦 𝑛 (Z^{x}_{n},Z^{y}_{n}) ( italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT , italic_Z start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT ) arbitrarily close to ( 0 , 0 ) 0 0 (0,0) ( 0 , 0 ) , which we discuss further in Section 6 . However, from Theorem 2 we infer that at least within the class of tests generated by ℱ ℱ \mathcal{F} caligraphic_F , this is necessary in order to attain the best worst-case power. In fact, more generally, we have the following result.

Theorem 3 .

There is no similar test of H 0 subscript 𝐻 0 H_{0} italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT against H 1 subscript 𝐻 1 H_{1} italic_H start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT with a rejection region that is bounded away from { ( δ x ∗ , δ y ∗ ) : δ x ∗ ⁢ δ y ∗ = 0 } conditional-set superscript subscript 𝛿 𝑥 superscript subscript 𝛿 𝑦 superscript subscript 𝛿 𝑥 superscript subscript 𝛿 𝑦 0 \{(\delta_{x}^{*},\delta_{y}^{*}):\delta_{x}^{*}\delta_{y}^{*}=0\} { ( italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT , italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT ) : italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT = 0 } .

Therefore, one cannot have a hypothesis test of H 0 subscript 𝐻 0 H_{0} italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT that is both similar/unbiased and that fails to reject for all values of ( Z n x , Z n y ) superscript subscript 𝑍 𝑛 𝑥 superscript subscript 𝑍 𝑛 𝑦 (Z_{n}^{x},Z_{n}^{y}) ( italic_Z start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT , italic_Z start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT ) that are arbitrarily close to the null hypothesis space; there is a fundamental trade-off between these two properties.

3.2 Dealing With Non-Unit Fraction Values of α 𝛼 \alpha italic_α

The rejection region R m ⁢ m subscript 𝑅 𝑚 𝑚 R_{mm} italic_R start_POSTSUBSCRIPT italic_m italic_m end_POSTSUBSCRIPT is only defined above for unit fractions α 𝛼 \alpha italic_α . For other values of α 𝛼 \alpha italic_α , the class of tests generated by ℱ ℱ \mathcal{F} caligraphic_F will not contain a similar test, though nonrandom similar tests may exist outside of this class. Tests at other values of α 𝛼 \alpha italic_α are typically of interest for two reasons: using multiple testing adjustment procedures and defining p 𝑝 p italic_p -values. We discuss the latter in the Supplementary Materials. The restriction that α 𝛼 \alpha italic_α must be a unit fraction is not a limitation for the Bonferroni correction procedure, which involves dividing the familywise error rate α 𝛼 \alpha italic_α by the number of tests, provided the familywise error rate α 𝛼 \alpha italic_α itself is a unit fraction. However, it is a limitation for the Benjamini–Hochberg procedure, which involves multiplying the false discovery rate α 𝛼 \alpha italic_α by a sequence of rational numbers, only some of which are unit fractions. We discuss the Benjamini–Hochberg procedure in Section 5 .

0=b_{-1}\leq b_{0}<b_{1}<\ldots<b_{\lfloor\alpha^{-1}\rfloor}=+\infty 0 = italic_b start_POSTSUBSCRIPT - 1 end_POSTSUBSCRIPT ≤ italic_b start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT < italic_b start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT < … < italic_b start_POSTSUBSCRIPT ⌊ italic_α start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT ⌋ end_POSTSUBSCRIPT = + ∞ . We define the rejection region α 𝛼 \alpha italic_α for any α ∈ ( 0 , 1 ) 𝛼 0 1 \alpha\in(0,1) italic_α ∈ ( 0 , 1 ) to be R m ⁢ m ′ := { ⋃ k = 0 ⌊ α − 1 ⌋ ( b k − 1 , b k ) × ( b k − 1 , b k ) } ∪ { ⋃ k = 0 ⌊ α − 1 ⌋ ( b k − 1 , b k ) × ( − b k , − b k − 1 ) } ∪ { ⋃ k = 0 ⌊ α − 1 ⌋ ( − b k , − b k − 1 ) × ( b k − 1 , b k ) } ∪ { ⋃ k = 0 ⌊ α − 1 ⌋ ( − b k , − b k − 1 ) × ( − b k , − b k − 1 ) } assign superscript subscript 𝑅 𝑚 𝑚 ′ superscript subscript 𝑘 0 superscript 𝛼 1 subscript 𝑏 𝑘 1 subscript 𝑏 𝑘 subscript 𝑏 𝑘 1 subscript 𝑏 𝑘 superscript subscript 𝑘 0 superscript 𝛼 1 subscript 𝑏 𝑘 1 subscript 𝑏 𝑘 subscript 𝑏 𝑘 subscript 𝑏 𝑘 1 superscript subscript 𝑘 0 superscript 𝛼 1 subscript 𝑏 𝑘 subscript 𝑏 𝑘 1 subscript 𝑏 𝑘 1 subscript 𝑏 𝑘 superscript subscript 𝑘 0 superscript 𝛼 1 subscript 𝑏 𝑘 subscript 𝑏 𝑘 1 subscript 𝑏 𝑘 subscript 𝑏 𝑘 1 R_{mm}^{\prime}:=\{\bigcup_{k=0}^{\lfloor\alpha^{-1}\rfloor}(b_{k-1},b_{k})% \times(b_{k-1},b_{k})\}\cup\{\bigcup_{k=0}^{\lfloor\alpha^{-1}\rfloor}(b_{k-1}% ,b_{k})\times(-b_{k},-b_{k-1})\}\cup\{\bigcup_{k=0}^{\lfloor\alpha^{-1}\rfloor% }(-b_{k},-b_{k-1})\times(b_{k-1},b_{k})\}\cup\{\bigcup_{k=0}^{\lfloor\alpha^{-% 1}\rfloor}(-b_{k},-b_{k-1})\times(-b_{k},-b_{k-1})\} italic_R start_POSTSUBSCRIPT italic_m italic_m end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT := { ⋃ start_POSTSUBSCRIPT italic_k = 0 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ⌊ italic_α start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT ⌋ end_POSTSUPERSCRIPT ( italic_b start_POSTSUBSCRIPT italic_k - 1 end_POSTSUBSCRIPT , italic_b start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ) × ( italic_b start_POSTSUBSCRIPT italic_k - 1 end_POSTSUBSCRIPT , italic_b start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ) } ∪ { ⋃ start_POSTSUBSCRIPT italic_k = 0 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ⌊ italic_α start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT ⌋ end_POSTSUPERSCRIPT ( italic_b start_POSTSUBSCRIPT italic_k - 1 end_POSTSUBSCRIPT , italic_b start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ) × ( - italic_b start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT , - italic_b start_POSTSUBSCRIPT italic_k - 1 end_POSTSUBSCRIPT ) } ∪ { ⋃ start_POSTSUBSCRIPT italic_k = 0 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ⌊ italic_α start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT ⌋ end_POSTSUPERSCRIPT ( - italic_b start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT , - italic_b start_POSTSUBSCRIPT italic_k - 1 end_POSTSUBSCRIPT ) × ( italic_b start_POSTSUBSCRIPT italic_k - 1 end_POSTSUBSCRIPT , italic_b start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ) } ∪ { ⋃ start_POSTSUBSCRIPT italic_k = 0 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ⌊ italic_α start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT ⌋ end_POSTSUPERSCRIPT ( - italic_b start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT , - italic_b start_POSTSUBSCRIPT italic_k - 1 end_POSTSUBSCRIPT ) × ( - italic_b start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT , - italic_b start_POSTSUBSCRIPT italic_k - 1 end_POSTSUBSCRIPT ) } . When α 𝛼 \alpha italic_α is a unit fraction, R m ⁢ m ′ subscript superscript 𝑅 ′ 𝑚 𝑚 R^{\prime}_{mm} italic_R start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_m italic_m end_POSTSUBSCRIPT coincides with R m ⁢ m subscript 𝑅 𝑚 𝑚 R_{mm} italic_R start_POSTSUBSCRIPT italic_m italic_m end_POSTSUBSCRIPT , hence R m ⁢ m ′ subscript superscript 𝑅 ′ 𝑚 𝑚 R^{\prime}_{mm} italic_R start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_m italic_m end_POSTSUBSCRIPT generates the minimax optimal test discussed earlier. Otherwise, the test generated by R m ⁢ m ′ subscript superscript 𝑅 ′ 𝑚 𝑚 R^{\prime}_{mm} italic_R start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_m italic_m end_POSTSUBSCRIPT corresponds closely to the minimax optimal test in that if δ y ∗ = 0 superscript subscript 𝛿 𝑦 0 \delta_{y}^{*}=0 italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT = 0 , then given Z ∗ x = z subscript superscript 𝑍 𝑥 𝑧 Z^{x}_{*}=z italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT = italic_z with z ∉ [ − b 0 , b 0 ] 𝑧 subscript 𝑏 0 subscript 𝑏 0 z\notin[-b_{0},b_{0}] italic_z ∉ [ - italic_b start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT , italic_b start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ] , the probability of being in the rejection region is exactly α 𝛼 \alpha italic_α . Precisely:

Theorem 4 .

The rejection region R m ⁢ m ′ superscript subscript 𝑅 𝑚 𝑚 ′ R_{mm}^{\prime} italic_R start_POSTSUBSCRIPT italic_m italic_m end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT is such that

				(7)

𝐾 1 1 𝑂 superscript 𝐾 2 \{4K(K+1)\}^{-1}=O(K^{-2}) { 4 italic_K ( italic_K + 1 ) } start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT = italic_O ( italic_K start_POSTSUPERSCRIPT - 2 end_POSTSUPERSCRIPT ) . Thus, the difference between the nominal and actual worst-case type 1 error is maximized at α = 3 / 4 𝛼 3 4 \alpha=3/4 italic_α = 3 / 4 , where the actual worst-case type 1 error is 5/8, 1/8 less than the nominal type 1 error. However, as noted, this maximal difference shrinks at a quadratic rate in ⌊ α − 1 ⌋ superscript 𝛼 1 \lfloor\alpha^{-1}\rfloor ⌊ italic_α start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT ⌋ , and is at most 1 / 1680 ≈ 0.0006 1 1680 0.0006 1/1680\approx 0.0006 1 / 1680 ≈ 0.0006 for all α < 0.05 𝛼 0.05 \alpha<0.05 italic_α < 0.05 .

3.3 Asymptotic approximation considerations

4 bayes risk optimal test.

We now consider a Bayes risk optimality criterion. We draw inspiration from and modify the testing procedure of Rosenblum et al., ( 2014 ) , which gives approximately Bayes risk optimal tests of an entirely different causal hypothesis. They were interested in simultaneously testing for treatment effects both in the overall population and in two subpopulations. Their approach was to discretize the test statistic space into a fine grid of cells, then cast the problem as a constrained optimization problem, where the unknown parameters to optimize over are the rejection probabilities in each cell, resulting in a rejection region that optimizes the Bayes risk they defined specific to their problem. This approach turns out to be easily adapted to our problem of testing the composite null hypothesis H 0 subscript 𝐻 0 H_{0} italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT .

We let M : ℝ 2 × [ 0 , 1 ] → { 0 , 1 } : 𝑀 → superscript ℝ 2 0 1 0 1 M:\mathbb{R}^{2}\times[0,1]\rightarrow\{0,1\} italic_M : blackboard_R start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT × [ 0 , 1 ] → { 0 , 1 } denote a generic testing function of H 0 subscript 𝐻 0 H_{0} italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT against H 1 subscript 𝐻 1 H_{1} italic_H start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT that characterizes the randomized test consisting of rejecting H 0 subscript 𝐻 0 H_{0} italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT for H 1 subscript 𝐻 1 H_{1} italic_H start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT if and only if M ⁢ ( Z ∗ x , Z ∗ y , U ) = 1 𝑀 subscript superscript 𝑍 𝑥 subscript superscript 𝑍 𝑦 𝑈 1 M(Z^{x}_{*},Z^{y}_{*},U)=1 italic_M ( italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT , italic_Z start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT , italic_U ) = 1 , where U 𝑈 U italic_U is a uniform random variable with support [ 0 , 1 ] 0 1 [0,1] [ 0 , 1 ] . As in Rosenblum et al., ( 2014 ) , it is purely for computational reasons that we consider a randomized test. Doing so yields a linear programming problem rather than an integer programming problem, the latter being far more computationally burdensome than the former, especially for our fairly high-dimensional optimization problem. However, our solution is almost entirely deterministic, with very few cells having non-degenerate rejection probabilities. Let L : { 0 , 1 } × ℝ 2 → ℝ : 𝐿 → 0 1 superscript ℝ 2 ℝ L:\{0,1\}\times\mathbb{R}^{2}\rightarrow\mathbb{R} italic_L : { 0 , 1 } × blackboard_R start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT → blackboard_R be a bounded loss function, and Λ Λ \Lambda roman_Λ denote a prior distribution on ( δ x ∗ , δ y ∗ ) superscript subscript 𝛿 𝑥 superscript subscript 𝛿 𝑦 (\delta_{x}^{*},\delta_{y}^{*}) ( italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT , italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT ) . We consider both a 0-1 loss function given by

and a (bounded) quadratic loss function given by

We consider 𝒩 ⁢ { 0 , 2 ⁢ Φ − 1 ⁢ ( 1 − α / 2 ) ⁢ 𝑰 𝟐 } 𝒩 0 2 superscript Φ 1 1 𝛼 2 subscript 𝑰 2 \mathcal{N}\{0,2\Phi^{-1}(1-\alpha/2)\bm{I_{2}}\} caligraphic_N { 0 , 2 roman_Φ start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT ( 1 - italic_α / 2 ) bold_italic_I start_POSTSUBSCRIPT bold_2 end_POSTSUBSCRIPT } for the prior Λ Λ \Lambda roman_Λ . The constrained Bayes optimization problem is the following: For given α ∈ ( 0 , 1 ) 𝛼 0 1 \alpha\in(0,1) italic_α ∈ ( 0 , 1 ) , L 𝐿 L italic_L , and Λ Λ \Lambda roman_Λ , find the function M 𝑀 M italic_M minimizing the Bayes risk

(8)

subject to the type 1 error constraint

(9)

8 𝐾 1 8K+1 8 italic_K + 1 inequalities, and the matrix characterizing the remaining probability constraints contains only one nonzero element per row.

The plots in Figure 2 show the solutions to the two linear approximation problems with α = 0.05 𝛼 0.05 \alpha=0.05 italic_α = 0.05 and K = 64 𝐾 64 K=64 italic_K = 64 .

For both tests, the rejection probabilities are nearly all zero or one. If one prefers a nonrandom test, one can obtain a slightly more conservative test by setting all nondegenerate probabilities to zero. Although we did not enforce symmetry in this particular implementation of the optimization problem, the plots are nonetheless almost completely symmetrical. Each test almost contains the entire rejection region of the joint significance test. Both rejection regions take interesting, somewhat unexpected shapes, with four roughly-symmetric disconnected regions inside of the acceptance region in the case of the 0-1 loss, and a single region inside the acceptance region centered around (0,0) in the case of the quadratic loss. As with the minimax optimal test, it seems that it is important to have part of the rejection region along the diagonals at least somewhat close to the origin, so that smaller alternatives in both δ x ∗ superscript subscript 𝛿 𝑥 \delta_{x}^{*} italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT and δ y ∗ superscript subscript 𝛿 𝑦 \delta_{y}^{*} italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT have larger rejection probabilities to offset the conservativeness induced by lying in the intersection of two acceptance region bands. As with the minimax optimal test, one might take issue with rejecting test statistics that are arbitrarily close to the null hypothesis space. We discuss this further in Section 6 .

While solving the linear programming problem to produce this test takes a nontrivial amount of time to run, this need only be done once, after which the object is stored and can be quickly loaded on demand. The approximate Bayes risk optimal tests can be solved for any size α ∈ ( 0 , 1 ) 𝛼 0 1 \alpha\in(0,1) italic_α ∈ ( 0 , 1 ) . However, the linear optimization problem must be solved separately for each value of α 𝛼 \alpha italic_α , and so cannot be obtained immediately.

As with the minimax optimal test, the approximate optimality of the tests defined in this section is in terms of the limiting distribution ( Z ∗ x , Z ∗ y ) superscript subscript 𝑍 𝑥 superscript subscript 𝑍 𝑦 (Z_{*}^{x},Z_{*}^{y}) ( italic_Z start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT , italic_Z start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT ) . Assuming uniform convergence of ( δ ^ x , δ ^ y ) subscript ^ 𝛿 𝑥 subscript ^ 𝛿 𝑦 (\hat{\delta}_{x},\hat{\delta}_{y}) ( over^ start_ARG italic_δ end_ARG start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT , over^ start_ARG italic_δ end_ARG start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT ) as in ( 1 ), the (sample) approximations to the (computational) approximate Bayes risk optimality objective functions and type 1 error constraints can be made arbitrarily small uniformly over the parameter space given a sufficiently large sample size. As with the minimax optimal test, the asymptotic approximation can be improved by replacing all instances of the normal distribution with the t 𝑡 t italic_t distribution with ( n − 1 ) 𝑛 1 (n-1) ( italic_n - 1 ) degrees of freedom.

5 LARGE-SCALE HYPOTHESIS TESTING

As mentioned above, applying the Bonferroni correction to the proposed methods in order to control for familywise error rate is straightforward even without the use of p 𝑝 p italic_p -values. For J 𝐽 J italic_J hypotheses, one can simply run any of the proposed tests with level α / J 𝛼 𝐽 \alpha/J italic_α / italic_J instead of comparing the p 𝑝 p italic_p -value to a threshold of α / J 𝛼 𝐽 \alpha/J italic_α / italic_J . Adapting the Benjamini–Hochberg procedure to control false discovery rate requires a bit more explanation if p 𝑝 p italic_p -values are not available (though the p 𝑝 p italic_p -value proposed in the Supplementary Materials can be used, which will be conservative). A modified Benjamini–Hochberg procedure works as follows: (i) find the largest value j 𝑗 j italic_j such that at least j 𝑗 j italic_j of the J 𝐽 J italic_J tests reject at α 𝛼 \alpha italic_α level α ⁢ j / J 𝛼 𝑗 𝐽 \alpha j/J italic_α italic_j / italic_J , (ii) reject all hypotheses that the test rejects at level α ⁢ j / J 𝛼 𝑗 𝐽 \alpha j/J italic_α italic_j / italic_J . It can be shown that this procedure controls the false discovery rate at α 𝛼 \alpha italic_α even for tests that are not monotone in α 𝛼 \alpha italic_α . A (potentially) conservative version of this procedure can avoid an exhaustive search for the largest j 𝑗 j italic_j in step (i). This procedure starts with j = 1 𝑗 1 j=1 italic_j = 1 and increases j 𝑗 j italic_j until fewer than α ⁢ j / J 𝛼 𝑗 𝐽 \alpha j/J italic_α italic_j / italic_J hypotheses are rejected for K 𝐾 K italic_K consecutive iterations for some pre-specified K 𝐾 K italic_K , after which the largest j 𝑗 j italic_j in this sequence at which at least α ⁢ j / J 𝛼 𝑗 𝐽 \alpha j/J italic_α italic_j / italic_J hypotheses are rejected is chosen for part (i).

One important and often overlooked point when testing for the presence of multiple mediated effects is that one needs to be willing to assume that the true mediators do not affect one another, which would result in some mediators being exposure-induced confounders, yielding the NIE non-identifiable (Avin et al.,, 2005 ) . This may not be realistic in many scenarios; however, this problem is beyond the scope of this article.

6 INTERPRETATION AND MODIFICATIONS

As we have pointed out, the rejection regions for the minimax and Bayes risk optimal tests have some peculiar features that some may regard as undesirable. Tests with such properties are known to arise in multi-parameter hypothesis testing and have received criticism in Perlman and Wu, ( 1999 ) as being flawed, though the philosophical debate about what criteria should be used to compare among statistical tests is perhaps not entirely settled (Berger,, 1999 ; McDermott and Wang,, 1999 ) . Rather than choosing a side on this debate, take a pluralistic stance and provide a menu of options, among which we hope anyone across this ideological spectrum can find a test that suits their preferences. Furthermore, we discuss differences in interpretation of different tests.

Not all of the criticisms of Perlman and Wu, ( 1999 ) apply to our tests, but at least two do. First, the minimax optimal test can reject when the point estimate is arbitrarily close to the null. How then is one to interpret a test that rejects when both test statistics are very small? One perspective is that a scientific investigator need not rely entirely on the result of a hypothesis test to determine whether an association or an effect is meaningful or “practically significant”, so long as the hypothesis test has correct type 1 error. Indeed, one could always pre-specify a minimally meaningful effect size, and never reject if the point estimate does not exceed it.

Second, the minimax optimal test is not monotonic in α 𝛼 \alpha italic_α , nor is it guaranteed that the Bayes risk optimal test is. In the Supplementary Materials, we introduce a p 𝑝 p italic_p -value corresponding to the minimax optimal test, which does not correspond one-to-one with the minimax optimal test. In fact, the p 𝑝 p italic_p -value can itself be used to define a new test that rejects at level α 𝛼 \alpha italic_α whenever the p 𝑝 p italic_p -value is less than α 𝛼 \alpha italic_α . A constrained variant of the Bayes risk optimal test can be devised for a given sequence of α 𝛼 \alpha italic_α values. This can be done by setting the rejection value to be no less (greater) than the largest (smallest) rejection probability among all tests with larger (smaller) α 𝛼 \alpha italic_α values preceding it in the sequence. Furthermore, the same realization of U 𝑈 U italic_U ought to be used across tests to preserve monotonicity.

To circumvent the first issue, we propose modifications of the minimax optimal and Bayes risk optimal tests. For the minimax optimal test and its corresponding p 𝑝 p italic_p -value-based test, one can simply truncate the rejection region according to any user-specified distance, say d 𝑑 d italic_d , from the null hypothesis space. For a test with rejection region R 𝑅 R italic_R , the rejection region of the corresponding truncated version will simply be R ∖ { ( Z n x , Z n y ) ⊤ : | Z n x | ∧ | Z n y | ≤ d } 𝑅 conditional-set superscript superscript subscript 𝑍 𝑛 𝑥 superscript subscript 𝑍 𝑛 𝑦 top superscript subscript 𝑍 𝑛 𝑥 superscript subscript 𝑍 𝑛 𝑦 𝑑 R\setminus\{(Z_{n}^{x},Z_{n}^{y})^{\top}:\lvert Z_{n}^{x}\rvert\wedge\lvert Z_% {n}^{y}\rvert\leq d\} italic_R ∖ { ( italic_Z start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT , italic_Z start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT ) start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT : | italic_Z start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT | ∧ | italic_Z start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT | ≤ italic_d } . The rejection region of the truncated minimax optimal test with d = 0.1 𝑑 0.1 d=0.1 italic_d = 0.1 is shown in panel (a) of Figure 3 . Of course, any cutoff can be chosen; we simply illustrate with 0.1 for the sake of comparison, because this is the distance of the rejection region of van Garderen and van Giersbergen, 2022a from the null hypothesis space.

Such truncated tests will clearly be dominated by their corresponding non-truncated versions in terms of power. A more powerful approach would be to instead optimize a constrained version of the minimax optimality criterion, where the constraint is that the test cannot reject for test statistics such that | Z n x | ∧ | Z n y | ≤ d superscript subscript 𝑍 𝑛 𝑥 superscript subscript 𝑍 𝑛 𝑦 𝑑 \lvert Z_{n}^{x}\rvert\wedge\lvert Z_{n}^{y}\rvert\leq d | italic_Z start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT | ∧ | italic_Z start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT | ≤ italic_d . This is a challenging problem that we do not address here, but that could be a fruitful direction for future research. One rebuttal to the claim of Perlman and Wu, ( 1999 ) that the rejection region ought to be bounded away from the null hypothesis space is that this distance is not specified, nor is there a clearly-defined criterion specifying what this distance should be (Berger,, 1999 ) . However, if one believes that this distance should be determined according to the likelihood ratio test, then one would set d 𝑑 d italic_d to be Φ − 1 ⁢ ( 1 − α / 2 ) superscript Φ 1 1 𝛼 2 \Phi^{-1}(1-\alpha/2) roman_Φ start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT ( 1 - italic_α / 2 ) , in which case the joint significance test, i.e., the likelihood ratio test (Liu et al.,, 2022 ; van Garderen and van Giersbergen, 2022a, ) , would be recovered in the single hypothesis test case, and our test offers nothing novel. However, if one is conducting multiple hypothesis testing and wishes to control for familywise error rate (for instance), and insists on a d 𝑑 d italic_d of Φ − 1 ⁢ ( 1 − α / 2 ) superscript Φ 1 1 𝛼 2 \Phi^{-1}(1-\alpha/2) roman_Φ start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT ( 1 - italic_α / 2 ) , then this does indeed generate a novel test with greatly-improved power over the Bonferroni-corrected joint significance test. For example, for a Bonferroni correction for 100 tests at level α = 0.05 𝛼 0.05 \alpha=0.05 italic_α = 0.05 , one can use the truncated minimax optimal test with α 𝛼 \alpha italic_α level 0.05 / 100 0.05 100 0.05/100 0.05 / 100 and with d = Φ − 1 ⁢ ( 1 − α / 2 ) 𝑑 superscript Φ 1 1 𝛼 2 d=\Phi^{-1}(1-\alpha/2) italic_d = roman_Φ start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT ( 1 - italic_α / 2 ) , which yields the rejection region in panel (b) of Figure 3 . In other words, one can apply the unmodified, but multiple testing-adjusted minimax optimal test, and then use the non-multiple testing-adjusted joint significance test as an additional test to screen out effects deemed too small. In this case, the Bonferroni-corrected minimax optimal test will have 100 times the worst-case power per test of that of the Bonferroni-corrected joint significance test, while still preserving familywise error rate and respecting the specified bound.

For the Bayes risk optimal tests, the same truncation could be easily applied. However, unlike the minimax optimal test, we also formulate a constrained version of the Bayes risk optimization problem in this article. For d = 0.1 𝑑 0.1 d=0.1 italic_d = 0.1 , the Bayes risk optimal test with 0-1 loss function will not change, since there is no part of the rejection region within 0.1 of the null hypothesis space. On the other hand, the Bayes risk optimal test with quadratic loss will change, since its rejection region contains a pixelated circle centered on the origin. The rejection region of the latter with d = 0.1 𝑑 0.1 d=0.1 italic_d = 0.1 is shown in the supplementary materials.

Another important challenge has to do with the traditional interpretation of a hypothesis test rejection decision: if the null hypothesis were true, then the probability of observing an event as or more extreme than the observed event is at most α 𝛼 \alpha italic_α . In multi-parameter hypothesis testing settings, this interpretation can be ambiguous, as there is not a total ordering in the parameter space. Nevertheless, in the product of coefficients case considered here, such an interpretation can be applied to a partial ordering, where one pair of test statistics is “as or more extreme” than another if both elements in the first pair are at least as large in magnitude as those in the second. van Garderen and van Giersbergen, 2022b refer to a test that rejects for all pairs of test statistics that are more extreme (in this sense) than another pair for which it also rejects as “information coherent”. Clearly none of the tests we have proposed nor the test of van Garderen and van Giersbergen, 2022a satisfy this property, hence these tests lack this traditional interpretation. Instead, they admit a weaker interpretation: if the null hypothesis were true, then the observed event would have been unlikely to occur in the sense that its rejection probability would be at most α 𝛼 \alpha italic_α . On the other hand, if the joint significance test and one of our proposed tests both reject, then the stronger interpretation can be applied. In a case where they disagree, then if one is applying one of our proposed tests, then one must be prepared to accept the possibility that one pair of test statistics that are smaller in magnitude may reject while another pair does not; this is entirely consistent with this weaker interpretation.

van Garderen and van Giersbergen, 2022b showed that the joint significance test is the most powerful test in the class of information coherent tests. Thus, there is a fundamental trade-off between gaining power over the joint significance test and preserving the former stronger interpretation over the latter weaker interpretation. If one deems the underpoweredness of the joint significance test to be an important problem, then one has no choice but to sacrifice a degree of interpretability. In proposing more powerful tests, we wish to present options to gain power at the cost of some interpretability for those who would deem it a worthwhile trade-off. One may reasonably feel uncomfortable making such a trade-off when scientific conclusions or policy decisions are to be based on the result. However, one may feel more comfortable with this trade-off in multiple hypothesis testing scenarios where the focus is on making multiple discoveries while controlling the number of errors. Thus, our proposed methodology is perhaps best suited for this latter setting.

7 SIMULATION STUDIES

7.1 single mediation hypothesis testing.

To compare the finite sample performances of our proposed tests with those of the delta method, joint significance, and van Garderen and van Giersbergen, 2022a (henceforth vGvG) tests, we performed a simulation study in which we sampled from independent t 𝑡 t italic_t distributions with noncentrality parameters ( δ x , δ y ) subscript 𝛿 𝑥 subscript 𝛿 𝑦 (\delta_{x},\delta_{y}) ( italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT , italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT ) . We considered four scenarios: (a) We varied δ x subscript 𝛿 𝑥 \delta_{x} italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT and δ y subscript 𝛿 𝑦 \delta_{y} italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT jointly from 0 to 0.4. (b) We fixed δ y subscript 𝛿 𝑦 \delta_{y} italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT to 0.2 and varied δ x subscript 𝛿 𝑥 \delta_{x} italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT from 0 to 0.4. (c) Using a normal approximation, we fixed δ y subscript 𝛿 𝑦 \delta_{y} italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT to 0 and varied δ x subscript 𝛿 𝑥 \delta_{x} italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT from 0 to 0.4, thereby exploring empirical type 1 error across a range of parameter values within the composite null hypothesis space. (d) We used the same setting as in (c), but using a t 𝑡 t italic_t -distribution with n − 1 𝑛 1 n-1 italic_n - 1 degrees of freedom approximation instead of the normal approximation. We drew 100,000 Monte Carlo samples with n = 50 𝑛 50 n=50 italic_n = 50 for each value of δ 𝛿 \delta italic_δ , and applied each test of H 0 : ` ⁢ ` ⁢ δ x ⁢ δ y = 0 ⁢ " : subscript 𝐻 0 ` ` subscript 𝛿 𝑥 subscript 𝛿 𝑦 0 " H_{0}:``\delta_{x}\delta_{y}=0" italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT : ` ` italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT = 0 " against H 1 : ` ⁢ ` ⁢ δ x ⁢ δ y ≠ 0 ⁢ " : subscript 𝐻 1 ` ` subscript 𝛿 𝑥 subscript 𝛿 𝑦 0 " H_{1}:``\delta_{x}\delta_{y}\neq 0" italic_H start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT : ` ` italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT ≠ 0 " to each sample. In particular, we used three versions of the Bayes risk optimal test: with the 0-1 loss function, with the quadratic loss function, and the constrained test with quadratic loss function. Likewise, we used three version of the minimax optimal test: the standard version, the test based on the corresponding p 𝑝 p italic_p -value defined in the Supplementary Materials, and a truncated minimax optimal test. In both the constrained and truncated tests, we used d = 0.1 𝑑 0.1 d=0.1 italic_d = 0.1 in order to make a fair comparison with the vGvG test, whose rejection region is 0.1 away from the null hypothesis space. The Monte Carlo power estimates are displayed in the plots in Figure 4 .


(a)		(b)

(c)		(d)

In scenario (a), apart from the minimax optimal p 𝑝 p italic_p -value-based test, all of the minimax optimal and Bayes risk optimal tests and the vGvG test have very close to nominal type 1 error at ( δ x , δ y ) = ( 0 , 0 ) subscript 𝛿 𝑥 subscript 𝛿 𝑦 0 0 (\delta_{x},\delta_{y})=(0,0) ( italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT , italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT ) = ( 0 , 0 ) . All of these tests greatly outperform the delta method and joint significance tests in terms of power for smaller values of δ x = δ y subscript 𝛿 𝑥 subscript 𝛿 𝑦 \delta_{x}=\delta_{y} italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT = italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT , with the minimax optimal p 𝑝 p italic_p -value-based test having power somewhere in between, but converging more quickly to the other tests. The delta method test remains very conservative over the entire range of parameter values. All of the tests except for the delta method test begin to converge in power closer to 0.4. The minimax optimal (apart from the p 𝑝 p italic_p -value based test), Bayes risk optimal, and vGvG tests perform very similarly over the range of parameter values, with the quadratic loss versions of the Bayes risk optimal test trading off some power loss in the 0.1–0.2 range for a slight improvement in power in the 0.3–0.4 range, demonstrating the greater emphasis the quadratic loss places on larger alternatives. The truncated minimax optimal test begins slightly conservative relative to 0.05, but catches up with the most powerful tests fairly quickly. Despite not being similar tests, the Bayes risk optimal and vGvG tests suffer very little in terms of power near the least favorable distribution at ( δ x , δ y ) = ( 0 , 0 ) subscript 𝛿 𝑥 subscript 𝛿 𝑦 0 0 (\delta_{x},\delta_{y})=(0,0) ( italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT , italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT ) = ( 0 , 0 ) .

In scenario (b), the trends are largely the same as in scenario (a). The main difference is that the quadratic loss versions of the Bayes risk optimal test are slightly conservative with respect to 0.05 under the null, albeit less conservative than the minimax optimal p 𝑝 p italic_p -value-based test. Once again, these tests trade off some power loss for smaller values of δ x subscript 𝛿 𝑥 \delta_{x} italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT (values less than about 0.25) for slightly improved power for larger values of δ x subscript 𝛿 𝑥 \delta_{x} italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT (from about 0.35–0.55). Since δ y subscript 𝛿 𝑦 \delta_{y} italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT is fixed at 0.2, power for all tests appears to plateau a little under 0.3. In scenarios (c) and (d), we see that all tests approximately preserve type 1 error; however, there is some anti-conservative behavior in scenario (c) due to the normal approximation being a bit too concentrated for a sample size of 50. This is corrected with the use of the t 𝑡 t italic_t -distribution approximation, which yields type 1 error much closer to 0.05 across the entire range of the null hypothesis parameter space we consider. In both cases, we see the performances of all tests except the delta method to converge by around δ x = 0.55 subscript 𝛿 𝑥 0.55 \delta_{x}=0.55 italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT = 0.55 .

7.2 Large-scale mediation hypothesis testing

Cutoff	Joint sig.				JT-comp				HDMT				Sobel-comp				DACT				MM-opt
e	0.	00	(0.	01)	1.	11	(0.	10)	1.	02	(0.	16)	0.	89	(0.	34)	1.	47	(1.	81)	1.	00	(0.	10)
e	0.	00	(0.	01)	1.	48	(0.	37)	1.	02	(0.	46)	0.	81	(0.	66)	2.	90	(4.	19)	1.	01	(0.	31)
e	0.	00	(0.	04)	3.	02	(1.	70)	1.	17	(1.	30)	1.	04	(1.	37)	6.	54	(10.	61)	1.	05	(1.	03)
e	0.	01	(0.	32)	9.	99	(10.	09)	1.	81	(4.	46)	1.	81	(4.	63)	16.	50	(31.	56)	1.	35	(3.	97)
e	0.	00	(0.	00)	15.	19	(17.	36)	2.	11	(6.	62)	2.	32	(7.	17)	22.	65	(47.	46)	1.	10	(4.	57)

8 DATA EXAMPLES

8.1 dctrs data analysis.

We applied our methodology to data from the Database of Cognitive Training and Remediation Studies (DCTRS), which consists of data from several randomized trials testing the efficacy of cognitive remediation therapy in patients with schizophrenia. Cognitive remediation therapy targets patients’ cognitive outcomes with the long-term goal of cognitive gains translating into improvements in more distal outcomes, such as functioning and quality of life. We used data from three trials described in Wykes et al., ( 1999 ) , Wykes et al., 2007a , and Wykes et al., 2007b , consisting of 128 patients with complete treatment, mediator, and outcome data. In each study, patients were randomized to a cognitive remediation therapy arm or a control arm. There are a number of issues (e.g., potential unobserved mediator-outcome confounding, variable follow-up time, and the fact that the data come from studies with different protocols) that we do not entirely account for in this analysis, and so our results should be viewed as purely illustrative of the proposed methodology.

Our exposure of interest, A 𝐴 A italic_A , was an indicator of whether the patient was assigned to the treatment arm; our outcome of interest, Y 𝑌 Y italic_Y , was the patient’s Rosenberg self-esteem scale score at follow-up, and the potential mediator of interest, M 𝑀 M italic_M , was the patient’s Wechsler Adult Intelligence Scale (WAIS) working memory digit span test at their end of treatment, which measures both working memory and attention. The mean self-esteem scale score was 33.6 with sample range from 17 to 50. Since the studies were all randomized trials, we only need to assume that variables included in 𝑪 𝑪 \bm{C} bold_italic_C and A 𝐴 A italic_A are sufficient to control for confounding of the effect of M 𝑀 M italic_M on Y 𝑌 Y italic_Y . We let 𝑪 𝑪 \bm{C} bold_italic_C consist of the patients’ sex, race, education, which study they participated in, and their self-esteem scale and working memory digit span test scores measured at baseline. We provide a more detailed discussion about the variable choices and modeling assumptions in the Supplementary Materials. Previously, Wykes et al., 2007b found cognitive remediation to improve working memory digit span test scores; Wykes et al., ( 1999 ) found cognitive remediation to improve self-esteem as measured by the Rosenberg self-esteem scale. We are testing whether there is an effect of cognitive remediation on patients’ self-esteem that is mediated by its effect on working memory and attention.

We fit models ( 2 ) and ( 4 ) using ordinary least squares, and estimated the natural indirect effect by the corresponding estimator given in Section 2 . We then applied the three versions of the minimax optimal test and the three versions of the Bayes risk optimal test from Section 7 , and compared these with the joint significance, delta method, and vGvG tests, all at level α = 0.05 𝛼 0.05 \alpha=0.05 italic_α = 0.05 , using the t-distribution approximation. The estimated natural indirect effect is 0.29, which is interpreted as cognitive remediation therapy modestly improving the self-esteem scale score by an average of 0.29 (0.04 standard deviations of the self-esteem scale score) through its effect on working memory and attention as measured by the digit span test.

Hypothesis test	Reject	-value
Bayes risk optimal, 0-1 loss	No	Undefined
Bayes risk optimal, quadratic loss	No	Undefined
Bayes risk optimal, quadratic loss, constrained	No	Undefined
Delta method	No	0.	256
Joint significance	No	0.	115
Minimax optimal	Yes	0.	039
Minimax optimal, truncated	Yes	0.	039
Minimax optimal, -value	Yes	0.	039
van Garderen and van Giersbergen	Yes	Undefined

The test statistic is plotted on the rejection regions of the minimax optimal and Bayes risk optimal tests in Figures S4–S8 of the Supplementary Materials.

Here we observe the improved power of the different versions of the minimax optimal test to reject the null hypothesis that the NIE is zero in favor of the alternative that it is nonzero. The interpretation for any of these tests is that if the true NIE were in fact zero, then the event we observed would have been unlikely to have occurred in the sense that the test would have rejected with at most 5% probability. Since these tests disagree with the joint significance test, they lack the stronger interpretation that the probability of observing an event as or more extreme would be at most 5% if the true NIE were zero. Having established that what we have observed is “unlikely” in the former sense, one may proceed by examining whether the estimated effect size is meaningful. An effect size of 0.04 standard deviations of the self-esteem scale score may not be deemed relevant for understanding the mechanism by which cognitive remediation therapy affects self-esteem. However, had the estimate been larger, one might conclude that there was a meaningful indirect effect through working memory, and that such an estimate would have been unlikely to have been observed if there were no true underlying indirect effect. In this case, neither of the traditional tests nor any of the Bayes risk optimal tests reject, but the vGvG test does reject, agreeing with the minimax optimal tests. While we have conducted nine tests for purposes of illustration, in practice one should decide a priori which test to use based on how they wish to navigate the power–interpretability trade-off to avoid data dredging.

8.2 Normative Aging Study Analysis

Liu et al., ( 2022 ) performed large-scale hypothesis testing on the Normative Aging Study (NAS) to test the mediated effect of smoking status on forced expiratory flow at 25%–75% of the Forced Expiratory Vital capacity, a measure of lung function, through 484,613 DNA methylation CpG cites among men in Eastern Massachusetts. We apply our proposed methodology to this same data and compare results. See Liu et al., ( 2022 ) for more details regarding this data. Based on the minimax optimal test with a Bonferroni correction controlling FWER at 0.05, we detect significant mediated effects through sites cg03636183, cg05575921, cg06126421, and cg21566642. The conservative version of the Benjamini–Hochberg correction controlling FDR at 0.05 additionally detected a mediated effect through the site cg05951221. The Bonferroni procedure ran locally on a MacBook Pro with 2.3 GHz Intel Core i5 in 7.3 seconds; the Benjamini–Hochberg procedure in 18.9 seconds. Liu et al., ( 2022 ) notes that each of these sites has previously been found to be related to smoking status and/or lung cancer risk. In comparison, the FDR-adjusted joint significance test identified all of these except cg05951221, while the FDR-adjusted DACT method of Liu et al., ( 2022 ) found all of these to be significant as well as 14 others, the latter of which they did not make any connections to previous findings in the literature.

9 DISCUSSION

We have proposed two novel classes of tests for the composite null hypothesis H 0 : ` ⁢ ` ⁢ δ x ⁢ δ y = 0 ⁢ " : subscript 𝐻 0 ` ` subscript 𝛿 𝑥 subscript 𝛿 𝑦 0 " H_{0}:``\delta_{x}\delta_{y}=0" italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT : ` ` italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT = 0 " against H 1 : ` ⁢ ` ⁢ δ x ⁢ δ y ≠ 0 ⁢ " : subscript 𝐻 1 ` ` subscript 𝛿 𝑥 subscript 𝛿 𝑦 0 " H_{1}:``\delta_{x}\delta_{y}\neq 0" italic_H start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT : ` ` italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT ≠ 0 " , which arises commonly in the context of mediation analysis. This is a challenging inferential task due to the non-uniform asymptotics of univariate test statistics of the product of coefficients, as well as the nonstandard structure of the null hypothesis space. We have constructed these tests to be both optimal in a decision theoretic sense, and to preserve type 1 error uniformly over the null hypothesis space—exactly so on both counts in the case of the minimax optimal test, and approximately so in the case of the Bayes risk optimal test. We have described procedures for carrying out large-scale hypothesis testing of many product-of-coefficient hypotheses, controlling for both familywise error rate and false discovery rate. We have also considered some shortcomings of these tests in terms of interpretability, and have developed modifications to remedy some of these shortcomings. Each of these comes at some cost of power, and we have illustrated a fundamental trade-off between the objectives of power and interpretability. Lastly, we have provided an R package to implement the minimax optimal test.

It is natural to ask which of the proposed tests should be used in practice. This is highly subjective, and depends on the criteria by which one judges hypothesis tests, as well as how much value one places on power in different parts of the alternative hypothesis space. We have introduced tests that improve on power of traditional tests, but not all of which have rejection regions bounded away from the null hypothesis space or that are monotonic in α 𝛼 \alpha italic_α . If one is only concerned with maximizing power subject to the constraint of uniformly preserving type 1 error, then these tests will be desirable. If one is concerned about the possibility of rejecting with small values of the test statistic, then one may employ a truncated or constrained version of these tests. If one finds the nonmonotocity property inadmissible, then one can use the test based on the p 𝑝 p italic_p -value corresponding to the minimax optimal test. If one is concerned about both, then one can use a truncated version of the p 𝑝 p italic_p -value based test. The minimax optimal test has the advantage of being a closed form exact solution to its corresponding optimization problem as well as preserving type 1 error exactly in the limit. The minimax optimal test also can be generated almost instantaneously for all unit fraction values of α 𝛼 \alpha italic_α , and the generalized test can be generated for other values of α 𝛼 \alpha italic_α , whereas for the Bayes risk optimal test, the optimization step to generate the rejection region must be performed each time a test for a new value of α 𝛼 \alpha italic_α is desired. p 𝑝 p italic_p -values are readily obtained for the minimax optimal test. Lastly, the minimax optimal test is a strictly deterministic test, whereas the Bayes risk optimal test contains a few cells in the rejection region that reject with non-degenerate probability. If a non-random test is desired, the latter can be converted to a slightly more conservative non-random test.

There are a number of important future research directions stemming from this work. There are many inferential problems that face similar issues with non-uniform convergence. Examples commonly arise in partial identification bounds, where there are often minima and maxima of estimates involved, which exhibit similar asymptotic behavior. The approaches proposed in this article can likely be adapted to such settings. Under different models, mediated effects can take the form of sums of products of coefficients. This considerably more complex setting will be important to address to allow for less restrictive models when performing inference on mediated effects. Lastly, we plan to further develop the tests for products of more than two coefficients discussed in the Supplementary Materials.

An R package implementing the minimax optimal test is available at https://github.com/achambaz/mediation.test .

ACKNOWLEDGMENTS

This publication was supported by the National Center for Advancing Translational Sciences, National Institutes of Health, through Grant Number KL2TR001874. The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH.

Avin et al., (2005) Avin, C., Shpitser, I., and Pearl, J. (2005). Identifiability of path-specific effects. In IJCAI-05, Proceedings of the Nineteenth International Joint Conference on Artificial Intelligence , pages 357–363.
Barfield et al., (2017) Barfield, R., Shen, J., Just, A. C., Vokonas, P. S., Schwartz, J., Baccarelli, A. A., VanderWeele, T. J., and Lin, X. (2017). Testing for the indirect effect under the null for genome-wide mediation analyses. Genetic Epidemiology , 41(8):824–833.
Baron and Kenny, (1986) Baron, R. M. and Kenny, D. A. (1986). The moderator–mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. Journal of Personality and Social Psychology , 51(6):1173.
Belloni et al., (2014) Belloni, A., Chernozhukov, V., and Hansen, C. (2014). Inference on treatment effects after selection among high-dimensional controls. The Review of Economic Studies , 81(2):608–650.
Berger, (1999) Berger, R. (1999). Comment on Perlman and Wu, “The Emperor’s New Tests” (with rejoinder by authors). Statistical Science , 14(4):370–381.
Cohen et al., (2013) Cohen, J., Cohen, P., West, S. G., and Aiken, L. S. (2013). Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences . Routledge.
Dai et al., (2020) Dai, J. Y., Stanford, J. L., and LeBlanc, M. (2020). A multiple-testing procedure for high-dimensional mediation hypotheses. Journal of the American Statistical Association , pages 1–16.
Ding and Vanderweele, (2016) Ding, P. and Vanderweele, T. J. (2016). Sharp sensitivity bounds for mediation under unmeasured mediator-outcome confounding. Biometrika , 103(2):483–490.
Du et al., (2023) Du, J., Zhou, X., Clark-Boucher, D., Hao, W., Liu, Y., Smith, J. A., and Mukherjee, B. (2023). Methods for large-scale single mediator hypothesis testing: Possible choices and comparisons. Genetic Epidemiology , 47(2):167–184.
Huang, (2019) Huang, Y.-T. (2019). Genome-wide analyses of sparse mediation effects under composite null hypotheses. The Annals of Applied Statistics , 13(1):60–84.
Imai et al., (2010) Imai, K., Keele, L., and Tingley, D. (2010). A general approach to causal mediation analysis. Psychological Methods , 15(4):309.
Kang et al., (2020) Kang, H., Lee, Y., Cai, T. T., and Small, D. S. (2020). Two robust tools for inference about causal effects with invalid instruments. Biometrics .
Lehmann et al., (2005) Lehmann, E. L., Romano, J. P., and Casella, G. (2005). Testing Statistical Hypotheses , volume 3. Springer.
Liu et al., (2022) Liu, Z., Shen, J., Barfield, R., Schwartz, J., Baccarelli, A. A., and Lin, X. (2022). Large-scale hypothesis testing for causal mediation effects with applications in genome-wide epigenetic studies. Journal of the American Statistical Association , 117(537):67–81.
MacKinnon et al., (2002) MacKinnon, D. P., Lockwood, C. M., Hoffman, J. M., West, S. G., and Sheets, V. (2002). A comparison of methods to test mediation and other intervening variable effects. Psychological Methods , 7(1):83.
McDermott and Wang, (1999) McDermott, M. P. and Wang, Y. (1999). [The Emperor’s New Tests]: Comment. Statistical Science , 14(4):374–377.
(17) Miles, C. H., Kanki, P., Meloni, S., and Tchetgen Tchetgen, E. J. (2017a). On partial identification of the natural indirect effect. Journal of Causal Inference , 5(2).
(18) Miles, C. H., Shpitser, I., Kanki, P., Meloni, S., and Tchetgen Tchetgen, E. J. (2017b). Quantifying an adherence path-specific effect of antiretroviral therapy in the Nigeria PEPFAR program. Journal of the American Statistical Association , 112(520):1443–1452.
Miles et al., (2020) Miles, C. H., Shpitser, I., Kanki, P., Meloni, S., and Tchetgen Tchetgen, E. J. (2020). On semiparametric estimation of a path-specific effect in the presence of mediator-outcome confounding. Biometrika , 107(1):159–172.
Perlman and Wu, (1999) Perlman, M. D. and Wu, L. (1999). The emperor’s new tests. Statistical Science , 14(4):355–369.
Robins and Ritov, (1997) Robins, J. M. and Ritov, Y. (1997). Toward a curse of dimensionality appropriate (CODA) asymptotic theory for semi-parametric models. Statistics in Medicine , 16(3):285–319.
Rosenblum et al., (2014) Rosenblum, M., Liu, H., and Yen, E.-H. (2014). Optimal tests of treatment effects for the overall population and two subpopulations in randomized trials, using sparse linear programming. Journal of the American Statistical Association , 109(507):1216–1228.
Sobel, (1982) Sobel, M. E. (1982). Asymptotic confidence intervals for indirect effects in structural equation models. Sociological Methodology , 13:290–312.
van Garderen and van Giersbergen, (2020) van Garderen, K. J. and van Giersbergen, N. (2020). Almost similar tests for mediation effects and other hypotheses with singularities. arXiv preprint arXiv:2012.11342 .
(25) van Garderen, K. J. and van Giersbergen, N. (2022a). A nearly similar powerful test for mediation. arXiv preprint arXiv:2012.11342 .
(26) van Garderen, K. J. and van Giersbergen, N. (2022b). On the optimality of the LR test for mediation. Symmetry , 14(1):178.
VanderWeele, (2015) VanderWeele, T. J. (2015). Explanation in Causal Inference: Methods for Mediation and Interaction . Oxford University Press.
VanderWeele and Vansteelandt, (2009) VanderWeele, T. J. and Vansteelandt, S. (2009). Conceptual issues concerning mediation, interventions and composition. Statistics and its Interface , 2:457–468.
Wright, (1921) Wright, S. (1921). Correlation and causation. Journal of Agricultural Research , 20(7):557–585.
(30) Wykes, T., Newton, E., Landau, S., Rice, C., Thompson, N., and Frangou, S. (2007a). Cognitive remediation therapy (CRT) for young early onset patients with schizophrenia: An exploratory randomized controlled trial. Schizophrenia Research , 94(1-3):221–230.
Wykes et al., (1999) Wykes, T., Reeder, C., Corner, J., Williams, C., and Everitt, B. (1999). The effects of neurocognitive remediation on executive processing in patients with schizophrenia. Schizophrenia Bulletin , 25(2):291–307.
(32) Wykes, T., Reeder, C., Landau, S., Everitt, B., Knapp, M., Patel, A., and Romeo, R. (2007b). Cognitive remediation therapy in schizophrenia: Randomised controlled trial. The British Journal of Psychiatry , 190(5):421–427.

SUPPLEMENTARY MATERIALS

Appendix a mediation analysis details.

The composite null hypothesis H 0 subscript 𝐻 0 H_{0} italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT arises naturally in mediation analysis under certain modeling assumptions. In order to define the indirect effect of interest, we first introduce notation. First, suppose we observe n 𝑛 n italic_n i.i.d. copies of ( 𝑪 ⊤ , A , M , Y ) ⊤ superscript superscript 𝑪 top 𝐴 𝑀 𝑌 top (\bm{C}^{\top},A,M,Y)^{\top} ( bold_italic_C start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT , italic_A , italic_M , italic_Y ) start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT , where A 𝐴 A italic_A is the exposure of interest, Y 𝑌 Y italic_Y is the outcome of interest, M 𝑀 M italic_M is a potential mediator that is temporally intermediate to A 𝐴 A italic_A and Y 𝑌 Y italic_Y , and 𝑪 𝑪 \bm{C} bold_italic_C is a vector of baseline covariates that we will assume throughout to be sufficient to control for various sorts of confounding needed for the indirect effect to be identified.

We now introduce counterfactuals in order to define the natural indirect effect. Let Y ⁢ ( a , m ) 𝑌 𝑎 𝑚 Y(a,m) italic_Y ( italic_a , italic_m ) be the counterfactual outcome that we would have observed (possibly contrary to fact) had A 𝐴 A italic_A been set to the level a 𝑎 a italic_a and M 𝑀 M italic_M been set to the level m 𝑚 m italic_m . Similarly, let M ⁢ ( a ) 𝑀 𝑎 M(a) italic_M ( italic_a ) be the counterfactual mediator value we would have observed (possibly contrary to fact) had A 𝐴 A italic_A been set to a 𝑎 a italic_a . Lastly, define the nested counterfactual Y ⁢ { a ′ , M ⁢ ( a ′′ ) } 𝑌 superscript 𝑎 ′ 𝑀 superscript 𝑎 ′′ Y\{a^{\prime},M(a^{\prime\prime})\} italic_Y { italic_a start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT , italic_M ( italic_a start_POSTSUPERSCRIPT ′ ′ end_POSTSUPERSCRIPT ) } to be the counterfactual outcome we would have observed had A 𝐴 A italic_A been set to a ′ superscript 𝑎 ′ a^{\prime} italic_a start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT and M 𝑀 M italic_M been set to the counterfactual value it would have taken had A 𝐴 A italic_A instead been set to a ′′ superscript 𝑎 ′′ a^{\prime\prime} italic_a start_POSTSUPERSCRIPT ′ ′ end_POSTSUPERSCRIPT . The natural direct effect (NDE) and natural indirect effect (NIE) on the difference scale are then defined to be

These additively decompose the total effect,

where Y ⁢ ( a ) 𝑌 𝑎 Y(a) italic_Y ( italic_a ) is the counterfactual outcome we would have observed (possibly contrary to fact) had A 𝐴 A italic_A been set to a 𝑎 a italic_a . Our focus will be on the natural indirect effect.

The natural indirect effect is nonparametrically identified under certain causal assumptions, viz., consistency, positivity, and a number of no unobserved confounding assumptions, which we will not review here for the sake of brevity and because our focus is on statistical inference rather than identification. These assumptions are well documented in the causal inference literature (see VanderWeele, ( 2015 ) for an overview). The identification formula for the natural indirect effect (also known as the mediation formula) is

where μ ⁢ ( m ) 𝜇 𝑚 \mu(m) italic_μ ( italic_m ) and μ ⁢ ( 𝒄 ) 𝜇 𝒄 \mu(\bm{c}) italic_μ ( bold_italic_c ) are dominating measures with respect to the distributions of M 𝑀 M italic_M and 𝑪 𝑪 \bm{C} bold_italic_C .

If the linear models with main effect terms given by

				(A.10)
				(A.11)

are correctly-specified, then the identification formula for the natural indirect effect reduces to β 1 ⁢ θ 2 subscript 𝛽 1 subscript 𝜃 2 \beta_{1}\theta_{2} italic_β start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT italic_θ start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT . The product method estimator estimates β 1 subscript 𝛽 1 \beta_{1} italic_β start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT and θ 2 subscript 𝜃 2 \theta_{2} italic_θ start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT by fitting the above regression models and takes the product of these coefficient estimates. In fact, following the path analysis literature of Wright, ( 1921 ) , Baron and Kenny, ( 1986 ) originally defined the indirect effect to be β 1 ⁢ θ 2 subscript 𝛽 1 subscript 𝜃 2 \beta_{1}\theta_{2} italic_β start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT italic_θ start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT , where 𝑪 𝑪 \bm{C} bold_italic_C is empty in the above model, rather than in terms of counterfactuals, and proposed the product method estimator. This is an extremely popular estimator of indirect effects. VanderWeele and Vansteelandt, ( 2009 ) demonstrated the consistency of the product method for the natural indirect effect under the above linear models. Under models ( A.10 ) and ( A.11 ) and standard regularity conditions, the two factors of the product method estimator will satisfy the uniform joint convergence statement in (1). In fact, (1) will hold for a more general class of models, though there are important limitations to this class. For instance, consider the outcome model with exposure-mediator interaction replacing model ( A.11 ):

(A.12)

subscript 𝜃 2 subscript 𝜃 3 superscript 𝑎 ′ \delta_{x}=\theta_{2}+\theta_{3}a^{\prime} italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT = italic_θ start_POSTSUBSCRIPT 2 end_POSTSUBSCRIPT + italic_θ start_POSTSUBSCRIPT 3 end_POSTSUBSCRIPT italic_a start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT and δ y = β 1 ⁢ ( a ′ − a ′′ ) subscript 𝛿 𝑦 subscript 𝛽 1 superscript 𝑎 ′ superscript 𝑎 ′′ \delta_{y}=\beta_{1}(a^{\prime}-a^{\prime\prime}) italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT = italic_β start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT ( italic_a start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT - italic_a start_POSTSUPERSCRIPT ′ ′ end_POSTSUPERSCRIPT ) and with the corresponding plug-in estimators for δ ^ x subscript ^ 𝛿 𝑥 \hat{\delta}_{x} over^ start_ARG italic_δ end_ARG start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT and δ ^ y subscript ^ 𝛿 𝑦 \hat{\delta}_{y} over^ start_ARG italic_δ end_ARG start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT . This is a key extension, as modern causal mediation analysis’ ability to account for the presence of exposure-mediator interactions is one of its important advantages over traditional mediation methods such as path analysis and the Baron and Kenny, ( 1986 ) approach. Unfortunately, the functional form of E ⁢ ( Y ∣ A = a , M = m , 𝑪 = 𝒄 ) 𝐸 formulae-sequence conditional 𝑌 𝐴 𝑎 formulae-sequence 𝑀 𝑚 𝑪 𝒄 E(Y\mid A=a,M=m,\bm{C}=\bm{c}) italic_E ( italic_Y ∣ italic_A = italic_a , italic_M = italic_m , bold_italic_C = bold_italic_c ) and E ⁢ ( M ∣ A = a , 𝑪 = 𝒄 ) 𝐸 formulae-sequence conditional 𝑀 𝐴 𝑎 𝑪 𝒄 E(M\mid A=a,\bm{C}=\bm{c}) italic_E ( italic_M ∣ italic_A = italic_a , bold_italic_C = bold_italic_c ) does not yield NIE estimators that factorize to satisfy (1) in general, as the identification formula can result in sums or integrals of products of coefficients. Handling models that yield such identification formulas will be an important direction in which to extend the work done in the present article. Extending the theory in the present article to more general settings than (1) is also especially important because mediated effects through multiple mediators can also be identified by sums of products of coefficients.

Appendix B Figure demonstrating the conservativeness of the asymptotic approximation to the true distributions of the delta method and joint significance tests

Appendix c plot of the power function surface of the minimax optimal test.

Appendix D Details of the Bayes risk optimization problem formulation

Under a random test defined by the rejection probabilities m r subscript 𝑚 𝑟 m_{r} italic_m start_POSTSUBSCRIPT italic_r end_POSTSUBSCRIPT on the squares in ℛ ℛ \mathcal{R} caligraphic_R , the Bayes risk in (8) decomposes as the sum

of which only the second term depends on ( m r ) r ∈ ℛ subscript subscript 𝑚 𝑟 𝑟 ℛ (m_{r})_{r\in\mathcal{R}} ( italic_m start_POSTSUBSCRIPT italic_r end_POSTSUBSCRIPT ) start_POSTSUBSCRIPT italic_r ∈ caligraphic_R end_POSTSUBSCRIPT , being equal to

From the above, the objective function is affine in the unknown variables ( m r ) r ∈ ℛ subscript subscript 𝑚 𝑟 𝑟 ℛ (m_{r})_{r\in\mathcal{R}} ( italic_m start_POSTSUBSCRIPT italic_r end_POSTSUBSCRIPT ) start_POSTSUBSCRIPT italic_r ∈ caligraphic_R end_POSTSUBSCRIPT .

We also define a discretized approximation of the type 1 error constraint (9). For each ( δ x ∗ , δ y ∗ ) ∈ G ′ superscript subscript 𝛿 𝑥 superscript subscript 𝛿 𝑦 superscript 𝐺 ′ (\delta_{x}^{*},\delta_{y}^{*})\in G^{\prime} ( italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT , italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT ) ∈ italic_G start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ,


				(D.13)

which is also affine in ( m r ) r ∈ ℛ subscript subscript 𝑚 𝑟 𝑟 ℛ (m_{r})_{r\in\mathcal{R}} ( italic_m start_POSTSUBSCRIPT italic_r end_POSTSUBSCRIPT ) start_POSTSUBSCRIPT italic_r ∈ caligraphic_R end_POSTSUBSCRIPT . Lastly, we need the probability constraints 0 ≤ m r ≤ 1 0 subscript 𝑚 𝑟 1 0\leq m_{r}\leq 1 0 ≤ italic_m start_POSTSUBSCRIPT italic_r end_POSTSUBSCRIPT ≤ 1 for all r ∈ ℛ 𝑟 ℛ r\in\mathcal{R} italic_r ∈ caligraphic_R . These inequalities along with ( D.13 ) define a linear optimization problem that approximates the Bayes risk optimization problem in ( m r ) r ∈ ℛ subscript subscript 𝑚 𝑟 𝑟 ℛ (m_{r})_{r\in\mathcal{R}} ( italic_m start_POSTSUBSCRIPT italic_r end_POSTSUBSCRIPT ) start_POSTSUBSCRIPT italic_r ∈ caligraphic_R end_POSTSUBSCRIPT , where all other terms are known.

Appendix E Minimax optimal test p 𝑝 p italic_p -values

A common definition of a p 𝑝 p italic_p -value for a simple null hypothesis is the probability of observing the same or more extreme values of the test statistic under the null hypothesis. For a composite null hypothesis, a p 𝑝 p italic_p -value may be defined similarly, but for the least-favorable distribution in the null hypothesis space. This definition is only useful when rejection regions for each α 𝛼 \alpha italic_α can be defined as level sets of some function of α 𝛼 \alpha italic_α , such that “more extreme” than a certain value can be taken to mean the set of values that the test always rejects whenever it rejects that particular value. The tests we have defined in this article admit no such representation. For instance, if ( Z n x , Z n y ) = ( Φ − 1 ⁢ ( 4 / 5 ) , Φ − 1 ⁢ ( 5 / 7 ) ) subscript superscript 𝑍 𝑥 𝑛 subscript superscript 𝑍 𝑦 𝑛 superscript Φ 1 4 5 superscript Φ 1 5 7 (Z^{x}_{n},Z^{y}_{n})=(\Phi^{-1}(4/5),\Phi^{-1}(5/7)) ( italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT , italic_Z start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_n end_POSTSUBSCRIPT ) = ( roman_Φ start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT ( 4 / 5 ) , roman_Φ start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT ( 5 / 7 ) ) , the minimax optimal test will reject H 0 subscript 𝐻 0 H_{0} italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT for H 1 subscript 𝐻 1 H_{1} italic_H start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT for α = 1 / 3 𝛼 1 3 \alpha=1/3 italic_α = 1 / 3 but not for α = 1 / 2 𝛼 1 2 \alpha=1/2 italic_α = 1 / 2 .

Alternatively, we adopt the more general definition of a p 𝑝 p italic_p -value as a statistic whose law stochastically dominates that of the uniform distribution with support [ 0 , 1 ] 0 1 [0,1] [ 0 , 1 ] for all distributions in the null hypothesis space. We can define a tentative p 𝑝 p italic_p -value to be p ^ := ∫ 0 1 I ⁢ { ( Z ∗ x , Z ∗ y ) ∉ R m ⁢ m ⁢ ( α ) } ⁢ 𝑑 α assign ^ 𝑝 superscript subscript 0 1 𝐼 subscript superscript 𝑍 𝑥 subscript superscript 𝑍 𝑦 subscript 𝑅 𝑚 𝑚 𝛼 differential-d 𝛼 \hat{p}:=\int_{0}^{1}I\{(Z^{x}_{*},Z^{y}_{*})\notin R_{mm}(\alpha)\}d\alpha over^ start_ARG italic_p end_ARG := ∫ start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT italic_I { ( italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT , italic_Z start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT ) ∉ italic_R start_POSTSUBSCRIPT italic_m italic_m end_POSTSUBSCRIPT ( italic_α ) } italic_d italic_α , where R m ⁢ m ⁢ ( α ) subscript 𝑅 𝑚 𝑚 𝛼 R_{mm}(\alpha) italic_R start_POSTSUBSCRIPT italic_m italic_m end_POSTSUBSCRIPT ( italic_α ) is the rejection region for a level α 𝛼 \alpha italic_α extended minimax optimal test. For the minimax optimal test, we use the extension of the minimax optimal test to non-unit fraction values of α 𝛼 \alpha italic_α described in Section 3.2. We conjecture that this will result in a valid p 𝑝 p italic_p -value in the sense that it will dominate the uniform distribution over [0,1] uniformly over the null hypothesis space. The plot in Figure S7 shows the empirical cumulative distribution function of a Monte Carlo sample of this p 𝑝 p italic_p -value for the minimax optimal test under the least-favorable distribution where ( δ x ∗ , δ y ∗ ) = ( 0 , 0 ) superscript subscript 𝛿 𝑥 superscript subscript 𝛿 𝑦 0 0 (\delta_{x}^{*},\delta_{y}^{*})=(0,0) ( italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT , italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT ) = ( 0 , 0 ) .

We can see that this cumulative distribution function does indeed dominate that of the uniform[0,1] distribution, and yet it is dominated by that of the p 𝑝 p italic_p -value corresponding to the joint-significance test. Having defined a p 𝑝 p italic_p -value corresponding to the extended minimax optimal test, one may use these p 𝑝 p italic_p -values to perform the Benjamini–Hochberg correction to many such independent tests to control the false discovery rate. When generating QQ-plots or volcano plots, no calibrations need to be made to the p 𝑝 p italic_p -values. A major distinction of our approach to large-scale mediation hypothesis testing from existing approaches is that we make no assumptions about the distribution of the parameters under the null hypothesis and do not attempt to estimate such a distribution. As such, our p 𝑝 p italic_p -values need to be valid under all parameter values under the composite null simultaneously, and we cannot recalibrate to get an exactly uniform distribution.

Since the extended minimax optimal test is conservative for non-unit fraction values of α 𝛼 \alpha italic_α , the p 𝑝 p italic_p -value will also be conservative. Thus, if one wishes to employ the standard minimax optimal test at a particular level of α 𝛼 \alpha italic_α , one would reject based on the test defined by the rejection region R m ⁢ m ⁢ ( α ) subscript 𝑅 𝑚 𝑚 𝛼 R_{mm}(\alpha) italic_R start_POSTSUBSCRIPT italic_m italic_m end_POSTSUBSCRIPT ( italic_α ) rather than comparing the p 𝑝 p italic_p -value to α 𝛼 \alpha italic_α , as these may not agree and the hypothesis test will be more powerful. However, as we discuss in the following section, one might prefer to instead define a test based on this p 𝑝 p italic_p -value.

Appendix F DCTRS data analysis details

F.1 table of baseline covariates.

Study 4155

(N=29)

Study 8134

(N=32)

Study 9212

(N=67)

F.2 Variable selection, causal assumptions, and statistical models

Although many additional measures of cognition and functioning at baseline are available in the data, we only included baseline measures of the WAIS working memory digit span test and the Rosenberg self-esteem scale for three reasons. The first is that since we are only concerned with controlling for confounding of the effect of working memory at the end of treatment on self-esteem at the end of follow-up, their corresponding baseline measures would seem to be the most relevant in terms of capturing baseline common causes from the cognition and functioning/quality-of-life domains. The second reason is that the sample size is not very large—certainly not large enough to include all baseline cognition and functioning measures—and so we favored a more parsimonious model that adjusted for the most relevant baseline measures of cognition and functioning/quality-of-life. The third is that many of these measures are not observed in all three studies. As is always the case with mediation analysis (even in the context of randomized experiments), our analyses are subject to bias due to residual confounding. Given that the purpose of this analysis is to illustrate our methodology, a full sensitivity analysis is beyond the scope of this article, though methods for such sensitivity analyses are available (Imai et al.,, 2010 ; Ding and Vanderweele,, 2016 ) , and will be important to incorporate into our testing procedures in future work. However, we do explore the impact of including additional covariates in 𝑪 𝑪 \bm{C} bold_italic_C in Section F.5 .

Another identification assumption for the NIE is that no common cause of M 𝑀 M italic_M and Y 𝑌 Y italic_Y is affected by A 𝐴 A italic_A , which, as is always the case in mediation analysis, may be violated in our study. However, this issue is also beyond the scope of this article. To address exposure-induced confounding, one could alternatively estimate partial identification bounds ( Miles et al., 2017a, ) , or focus on a different target estimand, such as the path-specific effect not through the exposure-induced confounder (Avin et al.,, 2005 ; Miles et al., 2017b, ; Miles et al.,, 2020 ) . Both approaches require observation of all exposure-induced confounders, say 𝑳 𝑳 \bm{L} bold_italic_L . The latter additionally requires the effect of A 𝐴 A italic_A on 𝑳 𝑳 \bm{L} bold_italic_L to itself have no residual confounding (which is guaranteed when A 𝐴 A italic_A is randomized), and no unobserved confounding of the effect of 𝑳 𝑳 \bm{L} bold_italic_L on M 𝑀 M italic_M and Y 𝑌 Y italic_Y . For a more detailed discussion on the assumptions needed to identify this path-specific effect, see Avin et al., ( 2005 ) and Miles et al., 2017b ; Miles et al., ( 2020 ) .

F.3 Plots of the bivariate test statistic from the DCTRS data analysis on the rejection regions corresponding to various tests

F.4 Analysis results by study

Hypothesis test	Reject	-value
Bayes risk optimal, 0-1 loss	No	Undefined
Bayes risk optimal, quadratic loss	No	Undefined
Bayes risk optimal, quadratic loss, constrained	No	Undefined
Delta method	No	0.	223
Joint significance	No	0.	164
Minimax optimal	No	0.	164
Minimax optimal, truncated	No	0.	164
Minimax optimal, -value	No	0.	164
van Garderen and van Giersbergen	No	Undefined

Hypothesis test	Reject	-value
Bayes risk optimal, 0-1 loss	No	Undefined
Bayes risk optimal, quadratic loss	No	Undefined
Bayes risk optimal, quadratic loss, constrained	Yes	Undefined
Delta method	No	0.	880
Joint significance	No	0.	859
Minimax optimal	No	0.	303
Minimax optimal, truncated	No	0.	303
Minimax optimal, -value	No	0.	303
van Garderen and van Giersbergen	No	Undefined

Hypothesis test	Reject	-value
Bayes risk optimal, 0-1 loss	No	Undefined
Bayes risk optimal, quadratic loss	No	Undefined
Bayes risk optimal, quadratic loss, constrained	No	Undefined
Delta method	No	0.	794
Joint significance	No	0.	749
Minimax optimal	No	0.	343
Minimax optimal, truncated	No	0.	343
Minimax optimal, -value	No	0.	343
van Garderen and van Giersbergen	No	Undefined

F.5 DCTRS analysis with additional baseline covariates

To assess the sensitivity to the choice of adjustment variables, we also conducted the analysis with additional covariates. In particular, we fit the linear models for the outcome and mediator including all variables available at baseline (after a round of imputation using random forest to fill in missing baseline covariates) using LASSO. We then augmented the adjustment set used in the initial analysis with the union of covariates selected in both LASSO fits, as motivated by the post-double-selection method of Belloni et al., ( 2014 ) for estimating average treatment effects. In our case, we only need to control for mediator-outcome confounding since the treatment is randomized, hence the determination of which variables to add to the adjustment set by models for the mediator and the outcome. When using “lambda.min” to tune the LASSO in glmnet (i.e., minimizing cross-validated error MSE), the selected variables consisted of the following baseline measurements: study ID, marital status, Rosenberg self-esteem scale (self-confirmation factor and total scores), Social Behaviour Scale (SBS) items: (attention-seeking behavior, coherence of conversation, concentration, depression, hostility/friendliness, personal appearance and hygiene, laughing and talking to self, socially unacceptable manners or habits, other behaviors that impede progress, panic attacks and phobias, slowness, verbal fluency test using the letters F, A, and S (FAS): total number of correct responses, trailmaking test part A (TMTA) (paper & pencil): number of errors, trailmaking test part B (TMTB) (paper & pencil): number of errors, Wechsler Adult Intelligence Scale (WAIS) (working memory digit span test raw score, picture completion raw and scaled scores, vocabulary raw score), Wisconsin Card Sorting Test (WCST): categories achieved, Positive and Negative Syndrome Scale (PANSS) items: P1 Delusions, P4 Excitement, P6 Suspiciousness, N5 Difficulty in Abstract Thinking, G2 Anxiety, G3 Guilt Feelings, G9 Unusual Thought Content, G12 Lack of Judgment and Insight, G16 Active Social Avoidance.

Augmenting our adjustment set with these variables yielded the results in Table 7 . Evidently, the results are indeed sensitive to which variables we adjust for. Rejection by more of the tests in this case could be a result of instability due to the number of covariates being adjusted for being large relative to the sample size. On the other hand, the fact that some of the tests failed to reject in the previous analysis could be a result of residual confounding bias. We cannot be sure of which is the case. However, it is certainly true that the validity of our proposed tests hinge on the validity of the identification assumptions.

Hypothesis test	Reject	-value
Bayes risk optimal, 0-1 loss	Yes	Undefined
Bayes risk optimal, quadratic loss	Yes	Undefined
Bayes risk optimal, quadratic loss, constrained	Yes	Undefined
Delta method	No	0.	127
Joint significance	Yes	0.	040
Minimax optimal	Yes	0.	034
Minimax optimal, truncated	Yes	0.	034
Minimax optimal, -value	Yes	0.	034
van Garderen and van Giersbergen	Yes	Undefined

Appendix G Tests of products of more than two coefficients

We now consider the more general hypothesis testing setting of H 0 ℓ : ` ⁢ ` ⁢ ∏ j = 1 ℓ δ j = 0 ⁢ " : superscript subscript 𝐻 0 ℓ ` ` superscript subscript product 𝑗 1 ℓ subscript 𝛿 𝑗 0 " H_{0}^{\ell}:``\prod_{j=1}^{\ell}\delta_{j}=0" italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT roman_ℓ end_POSTSUPERSCRIPT : ` ` ∏ start_POSTSUBSCRIPT italic_j = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT roman_ℓ end_POSTSUPERSCRIPT italic_δ start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT = 0 " against H 1 ℓ : ` ⁢ ` ⁢ ∏ j = 1 ℓ δ j ≠ 0 ⁢ " : superscript subscript 𝐻 1 ℓ ` ` superscript subscript product 𝑗 1 ℓ subscript 𝛿 𝑗 0 " H_{1}^{\ell}:``\prod_{j=1}^{\ell}\delta_{j}\neq 0" italic_H start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT roman_ℓ end_POSTSUPERSCRIPT : ` ` ∏ start_POSTSUBSCRIPT italic_j = 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT roman_ℓ end_POSTSUPERSCRIPT italic_δ start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ≠ 0 " when there exists an asymptotically normal estimator 𝜹 ^ := ( δ ^ 1 , … , δ ^ ℓ ) ⊤ assign bold-^ 𝜹 superscript subscript ^ 𝛿 1 … subscript ^ 𝛿 ℓ top \bm{\hat{\delta}}:=(\hat{\delta}_{1},\ldots,\hat{\delta}_{\ell})^{\top} overbold_^ start_ARG bold_italic_δ end_ARG := ( over^ start_ARG italic_δ end_ARG start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT , … , over^ start_ARG italic_δ end_ARG start_POSTSUBSCRIPT roman_ℓ end_POSTSUBSCRIPT ) start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT of 𝜹 := ( δ 1 , … , δ ℓ ) ⊤ assign 𝜹 superscript subscript 𝛿 1 … subscript 𝛿 ℓ top \bm{\delta}:=(\delta_{1},\ldots,\delta_{\ell})^{\top} bold_italic_δ := ( italic_δ start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT , … , italic_δ start_POSTSUBSCRIPT roman_ℓ end_POSTSUBSCRIPT ) start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT such that the convergence n ⁢ 𝚺 𝒏 − 1 / 2 ⁢ ( 𝜹 ^ − 𝜹 ) ↝ 𝒩 ⁢ ( 𝟎 ℓ , 𝑰 ℓ ) ↝ 𝑛 superscript subscript 𝚺 𝒏 1 2 bold-^ 𝜹 𝜹 𝒩 subscript 0 bold-ℓ subscript 𝑰 bold-ℓ \sqrt{n}\bm{\Sigma_{n}}^{-1/2}\left(\bm{\hat{\delta}}-\bm{\delta}\right)% \rightsquigarrow\mathcal{N}\left(\bm{0_{\ell}},\bm{I_{\ell}}\right) square-root start_ARG italic_n end_ARG bold_Σ start_POSTSUBSCRIPT bold_italic_n end_POSTSUBSCRIPT start_POSTSUPERSCRIPT - 1 / 2 end_POSTSUPERSCRIPT ( overbold_^ start_ARG bold_italic_δ end_ARG - bold_italic_δ ) ↝ caligraphic_N ( bold_0 start_POSTSUBSCRIPT bold_ℓ end_POSTSUBSCRIPT , bold_italic_I start_POSTSUBSCRIPT bold_ℓ end_POSTSUBSCRIPT ) is uniform in 𝜹 ∈ ℝ ℓ 𝜹 superscript ℝ ℓ \bm{\delta}\in\mathbb{R}^{\ell} bold_italic_δ ∈ blackboard_R start_POSTSUPERSCRIPT roman_ℓ end_POSTSUPERSCRIPT , where 𝚺 𝒏 subscript 𝚺 𝒏 \bm{\Sigma_{n}} bold_Σ start_POSTSUBSCRIPT bold_italic_n end_POSTSUBSCRIPT is again a consistent estimator of the asymptotic covariance matrix, 𝟎 ℓ subscript 0 bold-ℓ \bm{0_{\ell}} bold_0 start_POSTSUBSCRIPT bold_ℓ end_POSTSUBSCRIPT is the ℓ ℓ \ell roman_ℓ -vector of zeros, and 𝑰 ℓ subscript 𝑰 bold-ℓ \bm{I_{\ell}} bold_italic_I start_POSTSUBSCRIPT bold_ℓ end_POSTSUBSCRIPT is the ℓ × ℓ ℓ ℓ \ell\times\ell roman_ℓ × roman_ℓ identity matrix. This setting arises in linear structural equation modeling when one wishes to test the effect of an exposure along a chain of intermediate variables. Unfortunately, such effects are seldom identifiable in the causal mediation framework; however, this setting can arise in other applications as well. For instance, given multiple candidate instrumental variables, Kang et al., ( 2020 ) characterize the null hypothesis of no treatment effect and one valid instrument that is uncorrelated with the other candidates to be the product of multiple coefficients equaling zero.

The minimax optimal test lacks an obvious unique natural extension to the setting with more than two coefficients. Nevertheless, for unit fraction α 𝛼 \alpha italic_α , we can prove the existence of deterministic similar tests that are symmetric with respect to negations. For ℓ = 3 ℓ 3 \ell=3 roman_ℓ = 3 , these tests can be constructed using Latin squares of order α − 1 superscript 𝛼 1 \alpha^{-1} italic_α start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT . If the Latin square is totally symmetric, then the test will also be symmetric with respect to permutations. We only provide the result for ℓ = 3 ℓ 3 \ell=3 roman_ℓ = 3 ; however, we conjecture that these can be readily generalized to higher dimensions using Latin hypercubes, provided they exist for the choice of ℓ ℓ \ell roman_ℓ and α 𝛼 \alpha italic_α .

(G.14)

The test corresponding to R † superscript 𝑅 † R^{{\dagger}} italic_R start_POSTSUPERSCRIPT † end_POSTSUPERSCRIPT rejects H 0 ℓ superscript subscript 𝐻 0 ℓ H_{0}^{\ell} italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT roman_ℓ end_POSTSUPERSCRIPT for H 1 ℓ superscript subscript 𝐻 1 ℓ H_{1}^{\ell} italic_H start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT roman_ℓ end_POSTSUPERSCRIPT if ( | Z ∗ 1 | , | Z ∗ 2 | , | Z ∗ 3 | ) ⊤ ∈ R † superscript superscript subscript 𝑍 1 superscript subscript 𝑍 2 superscript subscript 𝑍 3 top superscript 𝑅 † (\lvert Z_{*}^{1}\rvert,\lvert Z_{*}^{2}\rvert,\lvert Z_{*}^{3}\rvert)^{\top}% \in R^{{\dagger}} ( | italic_Z start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT start_POSTSUPERSCRIPT 1 end_POSTSUPERSCRIPT | , | italic_Z start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT | , | italic_Z start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT start_POSTSUPERSCRIPT 3 end_POSTSUPERSCRIPT | ) start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT ∈ italic_R start_POSTSUPERSCRIPT † end_POSTSUPERSCRIPT .

Theorem 5 .

For any unit fraction α ∈ ( 0 , 1 ) 𝛼 0 1 \alpha\in(0,1) italic_α ∈ ( 0 , 1 ) and Latin square of order α − 1 superscript 𝛼 1 \alpha^{-1} italic_α start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT , 𝐀 𝐀 \bm{A} bold_italic_A , the corresponding test defined by the rejection region R † superscript 𝑅 † R^{{\dagger}} italic_R start_POSTSUPERSCRIPT † end_POSTSUPERSCRIPT in ( G.14 ) is a similar test of H 0 3 superscript subscript 𝐻 0 3 H_{0}^{3} italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT 3 end_POSTSUPERSCRIPT against H 1 3 superscript subscript 𝐻 1 3 H_{1}^{3} italic_H start_POSTSUBSCRIPT 1 end_POSTSUBSCRIPT start_POSTSUPERSCRIPT 3 end_POSTSUPERSCRIPT that is symmetric with respect to negations. If 𝐀 𝐀 \bm{A} bold_italic_A is totally symmetric, then the test is also symmetric with respect to permutations.

The Bayes risk optimal test can in theory also be extended to tests of products of ℓ ℓ \ell roman_ℓ coefficients. The grid in ℝ 2 superscript ℝ 2 \mathbb{R}^{2} blackboard_R start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT needs to be expanded to ℝ ℓ superscript ℝ ℓ \mathbb{R}^{\ell} blackboard_R start_POSTSUPERSCRIPT roman_ℓ end_POSTSUPERSCRIPT , and the grid on the null hypothesis space must be expanded to each of the ℝ ℓ − 1 superscript ℝ ℓ 1 \mathbb{R}^{\ell-1} blackboard_R start_POSTSUPERSCRIPT roman_ℓ - 1 end_POSTSUPERSCRIPT hyperplanes composing the new composite null hypothesis space. Further, the prior on the coefficients must be expanded to an ℓ ℓ \ell roman_ℓ -dimensional distribution. However, the computational burden will clearly escalate rapidly with ℓ ℓ \ell roman_ℓ , and may not be feasible even for dimensions of four or possibly even three without access to tremendous computing power and/or memory.

Appendix H Proofs

Proof of theorem 1..

When δ y ∗ = 0 subscript superscript 𝛿 𝑦 0 \delta^{*}_{y}=0 italic_δ start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT = 0 , for any δ x ∗ ∈ ℝ subscript superscript 𝛿 𝑥 ℝ \delta^{*}_{x}\in\mathbb{R} italic_δ start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT ∈ blackboard_R ,

The same holds for any δ y ∗ ∈ ℝ subscript superscript 𝛿 𝑦 ℝ \delta^{*}_{y}\in\mathbb{R} italic_δ start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT ∈ blackboard_R when δ x ∗ = 0 subscript superscript 𝛿 𝑥 0 \delta^{*}_{x}=0 italic_δ start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT = 0 by symmetry. Thus, (7) holds with R m ⁢ m subscript 𝑅 𝑚 𝑚 R_{mm} italic_R start_POSTSUBSCRIPT italic_m italic_m end_POSTSUBSCRIPT substituted for R 𝑅 R italic_R , and the test generated by the rejection region R m ⁢ m subscript 𝑅 𝑚 𝑚 R_{mm} italic_R start_POSTSUBSCRIPT italic_m italic_m end_POSTSUBSCRIPT is a similar test (because the null hypothesis space is its own boundary). ∎

Proof of Theorem 2.

For δ y ∗ = 0 subscript superscript 𝛿 𝑦 0 \delta^{*}_{y}=0 italic_δ start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT = 0 , we wish to find an R 𝑅 R italic_R such that for all δ x ∗ subscript superscript 𝛿 𝑥 \delta^{*}_{x} italic_δ start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT , we will have

which implies that E δ x ∗ ⁢ [ Pr δ y ∗ = 0 ⁢ { ( Z ∗ x , Z ∗ y ) ∈ R ∗ ∣ Z ∗ x } − α ] = 0 subscript 𝐸 subscript superscript 𝛿 𝑥 delimited-[] subscript Pr subscript superscript 𝛿 𝑦 0 conditional-set subscript superscript 𝑍 𝑥 subscript superscript 𝑍 𝑦 superscript 𝑅 subscript superscript 𝑍 𝑥 𝛼 0 E_{\delta^{*}_{x}}\left[\mathrm{Pr}_{\delta^{*}_{y}=0}\left\{(Z^{x}_{*},Z^{y}_% {*})\in R^{*}\mid Z^{x}_{*}\right\}-\alpha\right]=0 italic_E start_POSTSUBSCRIPT italic_δ start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT end_POSTSUBSCRIPT [ roman_Pr start_POSTSUBSCRIPT italic_δ start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT = 0 end_POSTSUBSCRIPT { ( italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT , italic_Z start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT ) ∈ italic_R start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT ∣ italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT } - italic_α ] = 0 for all δ x ∗ subscript superscript 𝛿 𝑥 \delta^{*}_{x} italic_δ start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT . Since Z ∗ x ∼ 𝒩 ⁢ ( δ x ∗ , 1 ) similar-to subscript superscript 𝑍 𝑥 𝒩 subscript superscript 𝛿 𝑥 1 Z^{x}_{*}\sim\mathcal{N}(\delta^{*}_{x},1) italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT ∼ caligraphic_N ( italic_δ start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT , 1 ) , which is a full-rank exponential family, Z ∗ x subscript superscript 𝑍 𝑥 Z^{x}_{*} italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT is a complete statistic, and

(H.15)

𝑘 1 𝛼 2 x>\Phi^{-1}\{\frac{1+(k+1)\alpha}{2}\} italic_x > roman_Φ start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT { divide start_ARG 1 + ( italic_k + 1 ) italic_α end_ARG start_ARG 2 end_ARG } .

Proof of Lemma 1 .

1 𝑘 𝛼 2 f(x_{0})=y_{0}>\Phi^{-1}(\frac{1+k\alpha}{2}) italic_f ( italic_x start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ) = italic_y start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT > roman_Φ start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT ( divide start_ARG 1 + italic_k italic_α end_ARG start_ARG 2 end_ARG ) for some

1 𝑘 𝛼 2 subscript 𝑦 0 x^{\prime}\in[\Phi^{-1}(\frac{1+k\alpha}{2}),y_{0}] italic_x start_POSTSUPERSCRIPT ′ end_POSTSUPERSCRIPT ∈ [ roman_Φ start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT ( divide start_ARG 1 + italic_k italic_α end_ARG start_ARG 2 end_ARG ) , italic_y start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT ] ,

𝑘 1 𝛼 2 x\allowbreak\in\allowbreak(\Phi^{-1}(\frac{1+k\alpha}{2}),\allowbreak\Phi^{-1}% \{\frac{1+(k+1)\alpha}{2}\}) italic_x ∈ ( roman_Φ start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT ( divide start_ARG 1 + italic_k italic_α end_ARG start_ARG 2 end_ARG ) , roman_Φ start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT { divide start_ARG 1 + ( italic_k + 1 ) italic_α end_ARG start_ARG 2 end_ARG } ) .

𝑘 1 𝛼 2 x\allowbreak>\allowbreak\Phi^{-1}\{\frac{1+(k+1)\alpha}{2}\} italic_x > roman_Φ start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT { divide start_ARG 1 + ( italic_k + 1 ) italic_α end_ARG start_ARG 2 end_ARG } . ∎

𝑘 1 𝛼 2 x\in(\Phi^{-1}(\frac{1+k\alpha}{2}),\Phi^{-1}\{\frac{1+(k+1)\alpha}{2}\}) italic_x ∈ ( roman_Φ start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT ( divide start_ARG 1 + italic_k italic_α end_ARG start_ARG 2 end_ARG ) , roman_Φ start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT { divide start_ARG 1 + ( italic_k + 1 ) italic_α end_ARG start_ARG 2 end_ARG } ) by induction. That is, f ⁢ ( x ) = a k − 1 𝑓 𝑥 subscript 𝑎 𝑘 1 f(x)=a_{k-1} italic_f ( italic_x ) = italic_a start_POSTSUBSCRIPT italic_k - 1 end_POSTSUBSCRIPT for all x ∈ ( a k − 1 , a k ) 𝑥 subscript 𝑎 𝑘 1 subscript 𝑎 𝑘 x\in(a_{k-1},a_{k}) italic_x ∈ ( italic_a start_POSTSUBSCRIPT italic_k - 1 end_POSTSUBSCRIPT , italic_a start_POSTSUBSCRIPT italic_k end_POSTSUBSCRIPT ) . Additionally, f ⁢ ( 0 ) = 0 𝑓 0 0 f(0)=0 italic_f ( 0 ) = 0 must hold. The only set of points on which we have not defined f 𝑓 f italic_f is

which is a set of measure zero. Thus, any function f 𝑓 f italic_f satisfying ( H.15 ) and hence generating a similar test must be equal to f m ⁢ m subscript 𝑓 𝑚 𝑚 f_{mm} italic_f start_POSTSUBSCRIPT italic_m italic_m end_POSTSUBSCRIPT everywhere except for the above set of measure zero. ∎

Proof of Theorem 3.

Suppose R † ⊂ ℝ 2 superscript 𝑅 † superscript ℝ 2 R^{{\dagger}}\subset\mathbb{R}^{2} italic_R start_POSTSUPERSCRIPT † end_POSTSUPERSCRIPT ⊂ blackboard_R start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT is a rejection region bounded away from { ( Z ∗ x , Z ∗ y ) : Z ∗ x ⁢ Z ∗ y = 0 } conditional-set subscript superscript 𝑍 𝑥 subscript superscript 𝑍 𝑦 subscript superscript 𝑍 𝑥 subscript superscript 𝑍 𝑦 0 \{(Z^{x}_{*},Z^{y}_{*}):Z^{x}_{*}Z^{y}_{*}=0\} { ( italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT , italic_Z start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT ) : italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT italic_Z start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT = 0 } . Then there is some ε > 0 𝜀 0 \varepsilon>0 italic_ε > 0 for which R † ∩ { ( Z ∗ x , Z ∗ y ) ⊤ : − ε < Z ∗ x < ε } = ∅ superscript 𝑅 † conditional-set superscript subscript superscript 𝑍 𝑥 subscript superscript 𝑍 𝑦 top 𝜀 subscript superscript 𝑍 𝑥 𝜀 R^{{\dagger}}\cap\{(Z^{x}_{*},Z^{y}_{*})^{\top}:-\varepsilon<Z^{x}_{*}<% \varepsilon\}=\emptyset italic_R start_POSTSUPERSCRIPT † end_POSTSUPERSCRIPT ∩ { ( italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT , italic_Z start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT ) start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT : - italic_ε < italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT < italic_ε } = ∅ . For all Z ∗ x ∈ ( − ε , ε ) subscript superscript 𝑍 𝑥 𝜀 𝜀 Z^{x}_{*}\in(-\varepsilon,\varepsilon) italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT ∈ ( - italic_ε , italic_ε ) , a set of positive measure, Pr ⁢ { ( Z ∗ x , Z ∗ y ) ⊤ ∈ R † ∣ Z ∗ x } = 0 Pr conditional-set superscript subscript superscript 𝑍 𝑥 subscript superscript 𝑍 𝑦 top superscript 𝑅 † subscript superscript 𝑍 𝑥 0 \mathrm{Pr}\left\{(Z^{x}_{*},Z^{y}_{*})^{\top}\in R^{{\dagger}}\mid Z^{x}_{*}% \right\}=0 roman_Pr { ( italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT , italic_Z start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT ) start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT ∈ italic_R start_POSTSUPERSCRIPT † end_POSTSUPERSCRIPT ∣ italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT } = 0 , hence ( H.15 ) does not hold for R † superscript 𝑅 † R^{{\dagger}} italic_R start_POSTSUPERSCRIPT † end_POSTSUPERSCRIPT . Thus, Pr ⁢ { ( Z ∗ x , Z ∗ y ) ⊤ ∈ R † } = 0.05 Pr superscript subscript superscript 𝑍 𝑥 subscript superscript 𝑍 𝑦 top superscript 𝑅 † 0.05 \mathrm{Pr}\left\{(Z^{x}_{*},Z^{y}_{*})^{\top}\in R^{{\dagger}}\right\}=0.05 roman_Pr { ( italic_Z start_POSTSUPERSCRIPT italic_x end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT , italic_Z start_POSTSUPERSCRIPT italic_y end_POSTSUPERSCRIPT start_POSTSUBSCRIPT ∗ end_POSTSUBSCRIPT ) start_POSTSUPERSCRIPT ⊤ end_POSTSUPERSCRIPT ∈ italic_R start_POSTSUPERSCRIPT † end_POSTSUPERSCRIPT } = 0.05 cannot hold for all ( δ x ∗ , δ y ∗ ) superscript subscript 𝛿 𝑥 superscript subscript 𝛿 𝑦 (\delta_{x}^{*},\delta_{y}^{*}) ( italic_δ start_POSTSUBSCRIPT italic_x end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT , italic_δ start_POSTSUBSCRIPT italic_y end_POSTSUBSCRIPT start_POSTSUPERSCRIPT ∗ end_POSTSUPERSCRIPT ) in H 0 subscript 𝐻 0 H_{0} italic_H start_POSTSUBSCRIPT 0 end_POSTSUBSCRIPT , and R † superscript 𝑅 † R^{{\dagger}} italic_R start_POSTSUPERSCRIPT † end_POSTSUPERSCRIPT does not generate a similar test. ∎

Proof of Theorem 4.

superscript 𝛼 1 superscript 𝛼 2 superscript 1 superscript 𝛼 1 𝛼 2 \lfloor\alpha^{-1}\rfloor\alpha^{2}+(1-\lfloor\alpha^{-1}\rfloor\alpha)^{2} ⌊ italic_α start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT ⌋ italic_α start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT + ( 1 - ⌊ italic_α start_POSTSUPERSCRIPT - 1 end_POSTSUPERSCRIPT ⌋ italic_α ) start_POSTSUPERSCRIPT 2 end_POSTSUPERSCRIPT . This completes the proof. ∎

Proof of Theorem 5 .

We may alternatively represent A 𝐴 A italic_A in its orthogonal array representation, which is an array with rows corresponding to each entry of A 𝐴 A italic_A consisting of the triple (row, column, symbol). Any permutation of the coordinates of these triples yields an orthogonal array corresponding to another Latin square known as a conjugate. Let A 132 superscript 𝐴 132 A^{132} italic_A start_POSTSUPERSCRIPT 132 end_POSTSUPERSCRIPT be the conjugate of A 𝐴 A italic_A generated by exchanging the second and third columns of the orthogonal array representation of A 𝐴 A italic_A . The region R † superscript 𝑅 † R^{{\dagger}} italic_R start_POSTSUPERSCRIPT † end_POSTSUPERSCRIPT can alternatively be expressed as

Clearly, the test is symmetric with respect to negations by construction. A Latin square is totally symmetric if it is equal to all of its conjugates. Thus, if A 𝐴 A italic_A is totally symmetric, then R † = R σ superscript 𝑅 † superscript 𝑅 𝜎 R^{{\dagger}}=R^{\sigma} italic_R start_POSTSUPERSCRIPT † end_POSTSUPERSCRIPT = italic_R start_POSTSUPERSCRIPT italic_σ end_POSTSUPERSCRIPT for all permutations σ 𝜎 \sigma italic_σ of (1,2,3), and the test corresponding to a totally symmetric Latin square is also symmetric with respect to permutations. ∎

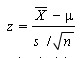
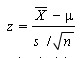
IMAGES

PPT
PPT
Significance Level and Power of a Hypothesis Test Tutorial
Solved If a null hypothesis is rejected at the 0.05 level of
when to reject or fail to reject null hypothesis Flashcards
Null hypothesis

VIDEO

Difference Between Null Hypothesis and Alternative Hypothesis
Hypothesis Testing: the null and alternative hypotheses
Hypothsis Testing in Statistics Part 2 Steps to Solving a Problem
What means to reject the null hypothesis?
When the null hypothesis is not rejected, there is no possibility of making a Type I error
If a difference is statistically significant, the null hypothesis was rejected

COMMENTS

When Do You Reject the Null Hypothesis? (3 Examples)
A hypothesis test is a formal statistical test we use to reject or fail to reject a statistical hypothesis. We always use the following steps to perform a hypothesis test: Step 1: State the null and alternative hypotheses. The null hypothesis, denoted as H0, is the hypothesis that the sample data occurs purely from chance.
What Is The Null Hypothesis & When To Reject It
When your p-value is less than or equal to your significance level, you reject the null hypothesis. In other words, smaller p-values are taken as stronger evidence against the null hypothesis. Conversely, when the p-value is greater than your significance level, you fail to reject the null hypothesis. In this case, the sample data provides ...
Null Hypothesis: Definition, Rejecting & Examples
When your sample contains sufficient evidence, you can reject the null and conclude that the effect is statistically significant. Statisticians often denote the null hypothesis as H 0 or H A.. Null Hypothesis H 0: No effect exists in the population.; Alternative Hypothesis H A: The effect exists in the population.; In every study or experiment, researchers assess an effect or relationship.
Hypothesis Testing
Let's return finally to the question of whether we reject or fail to reject the null hypothesis. If our statistical analysis shows that the significance level is below the cut-off value we have set (e.g., either 0.05 or 0.01), we reject the null hypothesis and accept the alternative hypothesis. Alternatively, if the significance level is above ...
Support or Reject Null Hypothesis in Easy Steps
Use the P-Value method to support or reject null hypothesis. Step 1: State the null hypothesis and the alternate hypothesis ("the claim"). H o:p ≤ 0.23; H 1:p > 0.23 (claim) Step 2: Compute by dividing the number of positive respondents from the number in the random sample: 63 / 210 = 0.3. Step 3: Find 'p' by converting the stated ...
Hypothesis Testing
Table of contents. Step 1: State your null and alternate hypothesis. Step 2: Collect data. Step 3: Perform a statistical test. Step 4: Decide whether to reject or fail to reject your null hypothesis. Step 5: Present your findings. Other interesting articles. Frequently asked questions about hypothesis testing.
6a.1
The first step in hypothesis testing is to set up two competing hypotheses. The hypotheses are the most important aspect. If the hypotheses are incorrect, your conclusion will also be incorrect. The two hypotheses are named the null hypothesis and the alternative hypothesis. The null hypothesis is typically denoted as H 0.
Understanding Null Hypothesis Testing
A crucial step in null hypothesis testing is finding the likelihood of the sample result if the null hypothesis were true. This probability is called the p value. A low p value means that the sample result would be unlikely if the null hypothesis were true and leads to the rejection of the null hypothesis. A high p value means that the sample ...
Null & Alternative Hypotheses
The null hypothesis is the claim that there's no effect in the population. If the sample provides enough evidence against the claim that there's no effect in the population (p ≤ α), then we can reject the null hypothesis. Otherwise, we fail to reject the null hypothesis. Although "fail to reject" may sound awkward, it's the only ...
16.3: The Process of Null Hypothesis Testing
Historically, the most common answer to this question has been that we should reject the null hypothesis if the p-value is less than 0.05. This comes from the writings of Ronald Fisher, who has been referred to as "the single most important figure in 20th century statistics" (Efron 1998) :
8.1: The null and alternative hypotheses
Alternative hypothesis. Alternative hypothesis $\left(H_{A}\right)$: If we conclude that the null hypothesis is false, or rather and more precisely, we find that we provisionally fail to reject the null hypothesis, then we provisionally accept the alternative hypothesis.The view then is that something other than random chance has influenced the sample observations.
4.4: Hypothesis Testing
Now if we obtain any observation with a Z score greater than 1.65, we would reject H 0. If the null hypothesis is true, we incorrectly reject the null hypothesis about 5% of the time when the sample mean is above the null value, as shown in Figure 4.19. Suppose the sample mean was smaller than the null value.
13.1 Understanding Null Hypothesis Testing
The logic of null hypothesis testing involves assuming that the null hypothesis is true, finding how likely the sample result would be if this assumption were correct, and then making a decision. If the sample result would be unlikely if the null hypothesis were true, then it is rejected in favor of the alternative hypothesis.
Null hypothesis
The null hypothesis and the alternative hypothesis are types of conjectures used in statistical tests to make statistical inferences, which are formal methods of reaching conclusions and separating scientific claims from statistical noise.. The statement being tested in a test of statistical significance is called the null hypothesis. The test of significance is designed to assess the strength ...
Failing to Reject the Null Hypothesis
There is something I am confused about. If our significance level is .05 and our resulting p-value is .02 (thus the strength of our evidence is strong enough to reject the null hypothesis), do we state that we reject the null hypothesis with 95% confidence or 98% confidence? My guess is our confidence level is 95% since or alpha was .05.
9.1 Null and Alternative Hypotheses
The actual test begins by considering two hypotheses.They are called the null hypothesis and the alternative hypothesis.These hypotheses contain opposing viewpoints. H 0, the —null hypothesis: a statement of no difference between sample means or proportions or no difference between a sample mean or proportion and a population mean or proportion. In other words, the difference equals 0.
S.3.1 Hypothesis Testing (Critical Value Approach)
The critical value for conducting the left-tailed test H0 : μ = 3 versus HA : μ < 3 is the t -value, denoted -t(α, n - 1), such that the probability to the left of it is α. It can be shown using either statistical software or a t -table that the critical value -t0.05,14 is -1.7613. That is, we would reject the null hypothesis H0 : μ = 3 in ...
Hypothesis Testing: Significance Level & Rejection Region
How big should Z be for us to reject the null hypothesis? Well, there is a cut-off line. Since we are conducting a two-sided or a two-tailed test, there are two cut-off lines, one on each side. When we calculate Z, we will get a value. If this value falls into the middle part, then we cannot reject the null.
9.1: Null and Alternative Hypotheses
Review. In a hypothesis test, sample data is evaluated in order to arrive at a decision about some type of claim.If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis, typically denoted with $H_{0}$.The null is not rejected unless the hypothesis test shows otherwise.
Understanding the Null Hypothesis for Linear Regression
x: The value of the predictor variable. Simple linear regression uses the following null and alternative hypotheses: H0: β1 = 0. HA: β1 ≠ 0. The null hypothesis states that the coefficient β1 is equal to zero. In other words, there is no statistically significant relationship between the predictor variable, x, and the response variable, y.
How To Reject a Null Hypothesis Using 2 Different Methods
1. Specify the null and alternative hypotheses. The first step in rejecting any null hypothesis involves stating the null and alternative hypotheses and separating them from each other. The null hypothesis takes the form of H0, while the alternative hypothesis takes the form of H1.
Hypothesis Testing: Upper-, Lower, and Two Tailed Tests
Because we rejected the null hypothesis, we now approximate the p-value which is the likelihood of observing the sample data if the null hypothesis is true. An alternative definition of the p-value is the smallest level of significance where we can still reject H 0. In this example, we observed Z=2.38 and for α=0.05, the critical value was 1.645.
What 'Fail to Reject' Means in a Hypothesis Test
Key Takeaways: The Null Hypothesis. • In a test of significance, the null hypothesis states that there is no meaningful relationship between two measured phenomena. • By comparing the null hypothesis to an alternative hypothesis, scientists can either reject or fail to reject the null hypothesis. • The null hypothesis cannot be positively ...
11.8: Significance Testing and Confidence Intervals
If the $95\%$ confidence interval contains zero (more precisely, the parameter value specified in the null hypothesis), then the effect will not be significant at the $0.05$ level. Looking at non-significant effects in terms of confidence intervals makes clear why the null hypothesis should not be accepted when it is not rejected: Every ...
Optimal Tests of the Composite Null Hypothesis Arising in Mediation
The remainder of the article is organized as follows. In Section 2, we formalize the problem and explain the shortcomings of traditional tests.In Sections 3 and 4, we present the minimax optimal and Bayes risk optimal test, respectively.In Section 5, we discuss adaptations for large-scale mediation hypothesis testing.In Section 6, we discuss interpretability challenges with the proposed tests ...

What is The Null Hypothesis & When Do You Reject The Null Hypothesis

How to Write a Null Hypothesis

For example, if studying the impact of exercise on weight loss, your null hypothesis might be:

Examples of Null Hypotheses

When Do We Reject The Null Hypothesis?

Why Do We Never Accept The Null Hypothesis?

Why Do We Use The Null Hypothesis?

Purpose of a Null Hypothesis

Do you always need both a Null Hypothesis and an Alternative Hypothesis?

What is the difference between a null hypothesis and an alternative hypothesis?

What are some problems with the null hypothesis?

Why can a null hypothesis not be accepted?

Is a null hypothesis directional or non-directional?

Hypothesis Testing (cont...)

Significance levels

One- and two-tailed predictions

Rejecting or failing to reject the null hypothesis

Support or Reject Null Hypothesis in Easy Steps

To reject the null hypothesis, perform the following steps:

When to Reject the Null hypothesis

Support or Reject the Null Hypothesis: Steps

Support or Reject Null Hypothesis with a P Value

P-Value Guidelines

Support or Reject Null Hypothesis for a Proportion

Support or Reject Null Hypothesis for a Proportion: Second example

Understanding Null Hypothesis Testing

The Purpose of Null Hypothesis Testing

The Logic of Null Hypothesis Testing

Role of Sample Size and Relationship Strength

Statistical Significance Versus Practical Significance

Long Descriptions

Media Attributions

Share This Book

Have a language expert improve your writing

Null & Alternative Hypotheses | Definitions, Templates & Examples

Table of contents

Receive feedback on language, structure, and formatting

Examples of null hypotheses

Examples of alternative hypotheses

Prevent plagiarism. Run a free check.

General template sentences

Test-specific template sentences

Cite this Scribbr article

Is this article helpful?

Shaun Turney

13.1 Understanding Null Hypothesis Testing

The Purpose of Null Hypothesis Testing

The Logic of Null Hypothesis Testing

The Misunderstood p Value

Role of Sample Size and Relationship Strength

Statistical Significance Versus Practical Significance

Key Takeaways

Share This Book

Failing to Reject the Null Hypothesis

Why Don’t Statisticians Accept the Null Hypothesis?

Species Presumed to be Extinct

Criminal Trials

Hypothesis Tests

What Does Fail to Reject the Null Hypothesis Mean?

Share this:

Reader Interactions

Comments and Questions Cancel reply

9.1 Null and Alternative Hypotheses

Example 9.1

Example 9.2

Example 9.3

Example 9.4

Collaborative Exercise

User Preferences

Keyboard Shortcuts

Example S.3.1.1

Right-Tailed

Left-Tailed

Hypothesis Testing with Z-Test: Significance Level and Rejection Region

What Is the Significance Level?

How Is the Significance Level Denoted?

A Case in Point

Higher Degree of Error

Hypothesis Testing: Performing a Z-Test

Visualizing the Grades