Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.

Under what condition, the optimal solution of assignment problem is unique?
Is there any conditions that can make the optimal solution of a assignment problem unique?
I know if there is no conditions on the cost matrix, it is not guaranteed to have a unique solution. (e.g. if a cost matrix has same number on all entries, then any assignments is optimal.)
References will also be welcomed. Thank you!
- reference-request
- optimization
- integer-programming
- discrete-optimization
This question is answered in detail in section 5.3 of Assignment Problems (Burkard, Dell'Amico, Martello) . Also see: Burkard & Butkovič (2003) "Max algebra and the linear assignment problem." Mathematical Programming 98, 415–429.
Unfortunately, all of these results are approachable but difficult to concisely summarize (for me at least).
Note that, assuming a square cost matrix $C$ , all solutions to the linear assignment problem are basic feasible solutions (i.e. solutions lying on a vertex of the constraint set) of a the following linear program:
\begin{equation*} \begin{aligned} & \underset{x}{\text{minimize}} & & \sum_{ij} C_{ij} P_{ij} \\ & \text{subject to} & & P_{ij} \geq 0, \quad \sum_i P_{ij} = 1, \quad \sum_j P_{ij} = 1 \end{aligned} \end{equation*}
The feasible set here is the Birkhoff polytope which is the convex hull of the set of all permutation matrices (due to the Birkhoff–von Neumann theorem). In this setting, the solution to an assignment problem will be unique if and only if the solution to this linear program is unique. Sufficient and necessary conditions for the uniqueness of linear programs can be found in, e.g., Mangasarian (1979) "Uniqueness of solution in linear programming." Linear Algebra and its Applications 25, 151-162.
You must log in to answer this question.
Not the answer you're looking for browse other questions tagged reference-request optimization integer-programming discrete-optimization ..
- Upcoming Events
- 2024 Community Moderator Election ends in 12 hours
- Featured on Meta
- We've made changes to our Terms of Service & Privacy Policy - July 2024
- Bringing clarity to status tag usage on meta sites
- Upcoming Moderator Election
- 2024 Community Moderator Election
Hot Network Questions
- Using 尊敬語 and 謙譲語 without 丁寧語?
- Did the French janitor at the University of Hanoi receive a higher base pay than a Vietnamese professor?
- Finite loop runs infinitely
- Ecuador: what not to take into the rainforest due to humidity?
- Capacitor package selection for DC-DC convertor
- Is there a good explanation for the existence of the C19 globular cluster with its very low metallicity?
- Choosing a relative large density subsequence from a low density sequence
- White to play and mate in 3 moves..what are the moves?
- How can I understand op-amp operation modes?
- Did anyone ever ask Neil Armstrong whether he said "for man" or "for a man?"
- Are "lie low" and "keep a low profile" interchangeable?
- No Kippa while in a car
- A schema for awallet system that allows transfers between users
- A natural automorphism of a finite group with two generators?
- How did this zucchini plant cling to the zip tie?
- Does "any computer(s) you have" refer to one or all the computers?
- What is the rationale behind requiring ATC to retire at age 56?
- Trigger (after delete) restricts from deleting records
- Möbius square root function: existence of multiplicative and bounded function
- Creating a deadly "minimum altitude limit" in an airship setting
- Rounding vertices of polygon to fixed number of decimal places in QGIS
- Adverb for Lore?
- Can data be preprocessed when using EdDSA with SHAKE?
- What is this surface feature near Shackleton crater classified as?

How to Solve the Assignment Problem: A Complete Guide
Table of Contents
Assignment problem is a special type of linear programming problem that deals with assigning a number of resources to an equal number of tasks in the most efficient way. The goal is to minimize the total cost of assignments while ensuring that each task is assigned to only one resource and each resource is assigned to only one task. In this blog, we will discuss the solution of the assignment problem using the Hungarian method, which is a popular algorithm for solving the problem.
Understanding the Assignment Problem
Before we dive into the solution, it is important to understand the problem itself. In the assignment problem, we have a matrix of costs, where each row represents a resource and each column represents a task. The objective is to assign each resource to a task in such a way that the total cost of assignments is minimized. However, there are certain constraints that need to be satisfied – each resource can be assigned to only one task and each task can be assigned to only one resource.
Solving the Assignment Problem
There are various methods for solving the assignment problem, including the Hungarian method, the brute force method, and the auction algorithm. Here, we will focus on the steps involved in solving the assignment problem using the Hungarian method, which is the most commonly used and efficient method.
Step 1: Set up the cost matrix
The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent. The matrix should be square and have the same number of rows and columns as the number of tasks and agents, respectively.
Step 2: Subtract the smallest element from each row and column
To simplify the calculations, we need to reduce the size of the cost matrix by subtracting the smallest element from each row and column. This step is called matrix reduction.
Step 3: Cover all zeros with the minimum number of lines
The next step is to cover all zeros in the matrix with the minimum number of horizontal and vertical lines. This step is called matrix covering.
Step 4: Test for optimality and adjust the matrix
To test for optimality, we need to calculate the minimum number of lines required to cover all zeros in the matrix. If the number of lines equals the number of rows or columns, the solution is optimal. If not, we need to adjust the matrix and repeat steps 3 and 4 until we get an optimal solution.
Step 5: Assign the tasks to the agents
The final step is to assign the tasks to the agents based on the optimal solution obtained in step 4. This will give us the most cost-effective or profit-maximizing assignment.
Solution of the Assignment Problem using the Hungarian Method
The Hungarian method is an algorithm that uses a step-by-step approach to find the optimal assignment. The algorithm consists of the following steps:
- Subtract the smallest entry in each row from all the entries of the row.
- Subtract the smallest entry in each column from all the entries of the column.
- Draw the minimum number of lines to cover all zeros in the matrix. If the number of lines drawn is equal to the number of rows, we have an optimal solution. If not, go to step 4.
- Determine the smallest entry not covered by any line. Subtract it from all uncovered entries and add it to all entries covered by two lines. Go to step 3.
The above steps are repeated until an optimal solution is obtained. The optimal solution will have all zeros covered by the minimum number of lines. The assignments can be made by selecting the rows and columns with a single zero in the final matrix.
Applications of the Assignment Problem
The assignment problem has various applications in different fields, including computer science, economics, logistics, and management. In this section, we will provide some examples of how the assignment problem is used in real-life situations.
Applications in Computer Science
The assignment problem can be used in computer science to allocate resources to different tasks, such as allocating memory to processes or assigning threads to processors.
Applications in Economics
The assignment problem can be used in economics to allocate resources to different agents, such as allocating workers to jobs or assigning projects to contractors.
Applications in Logistics
The assignment problem can be used in logistics to allocate resources to different activities, such as allocating vehicles to routes or assigning warehouses to customers.
Applications in Management
The assignment problem can be used in management to allocate resources to different projects, such as allocating employees to tasks or assigning budgets to departments.
Let’s consider the following scenario: a manager needs to assign three employees to three different tasks. Each employee has different skills, and each task requires specific skills. The manager wants to minimize the total time it takes to complete all the tasks. The skills and the time required for each task are given in the table below:
| Task 1 | Task 2 | Task 3 | |
|---|---|---|---|
| Emp 1 | 5 | 7 | 6 |
| Emp 2 | 6 | 4 | 5 |
| Emp 3 | 8 | 5 | 3 |
The assignment problem is to determine which employee should be assigned to which task to minimize the total time required. To solve this problem, we can use the Hungarian method, which we discussed in the previous blog.
Using the Hungarian method, we first subtract the smallest entry in each row from all the entries of the row:
| Task 1 | Task 2 | Task 3 | |
|---|---|---|---|
| Emp 1 | 0 | 2 | 1 |
| Emp 2 | 2 | 0 | 1 |
| Emp 3 | 5 | 2 | 0 |
Next, we subtract the smallest entry in each column from all the entries of the column:
| Task 1 | Task 2 | Task 3 | |
|---|---|---|---|
| Emp 1 | 0 | 2 | 1 |
| Emp 2 | 2 | 0 | 1 |
| Emp 3 | 5 | 2 | 0 |
| 0 | 0 | 0 |
We draw the minimum number of lines to cover all the zeros in the matrix, which in this case is three:
Since the number of lines is equal to the number of rows, we have an optimal solution. The assignments can be made by selecting the rows and columns with a single zero in the final matrix. In this case, the optimal assignments are:
- Emp 1 to Task 3
- Emp 2 to Task 2
- Emp 3 to Task 1
This assignment results in a total time of 9 units.
I hope this example helps you better understand the assignment problem and how to solve it using the Hungarian method.
Solving the assignment problem may seem daunting, but with the right approach, it can be a straightforward process. By following the steps outlined in this guide, you can confidently tackle any assignment problem that comes your way.
How useful was this post?
Click on a star to rate it!
Average rating 0 / 5. Vote count: 0
No votes so far! Be the first to rate this post.
We are sorry that this post was not useful for you! 😔
Let us improve this post!
Tell us how we can improve this post?
Operations Research
1 Operations Research-An Overview
- History of O.R.
- Approach, Techniques and Tools
- Phases and Processes of O.R. Study
- Typical Applications of O.R
- Limitations of Operations Research
- Models in Operations Research
- O.R. in real world
2 Linear Programming: Formulation and Graphical Method
- General formulation of Linear Programming Problem
- Optimisation Models
- Basics of Graphic Method
- Important steps to draw graph
- Multiple, Unbounded Solution and Infeasible Problems
- Solving Linear Programming Graphically Using Computer
- Application of Linear Programming in Business and Industry
3 Linear Programming-Simplex Method
- Principle of Simplex Method
- Computational aspect of Simplex Method
- Simplex Method with several Decision Variables
- Two Phase and M-method
- Multiple Solution, Unbounded Solution and Infeasible Problem
- Sensitivity Analysis
- Dual Linear Programming Problem
4 Transportation Problem
- Basic Feasible Solution of a Transportation Problem
- Modified Distribution Method
- Stepping Stone Method
- Unbalanced Transportation Problem
- Degenerate Transportation Problem
- Transhipment Problem
- Maximisation in a Transportation Problem
5 Assignment Problem
- Solution of the Assignment Problem
- Unbalanced Assignment Problem
- Problem with some Infeasible Assignments
- Maximisation in an Assignment Problem
- Crew Assignment Problem
6 Application of Excel Solver to Solve LPP
- Building Excel model for solving LP: An Illustrative Example
7 Goal Programming
- Concepts of goal programming
- Goal programming model formulation
- Graphical method of goal programming
- The simplex method of goal programming
- Using Excel Solver to Solve Goal Programming Models
- Application areas of goal programming
8 Integer Programming
- Some Integer Programming Formulation Techniques
- Binary Representation of General Integer Variables
- Unimodularity
- Cutting Plane Method
- Branch and Bound Method
- Solver Solution
9 Dynamic Programming
- Dynamic Programming Methodology: An Example
- Definitions and Notations
- Dynamic Programming Applications
10 Non-Linear Programming
- Solution of a Non-linear Programming Problem
- Convex and Concave Functions
- Kuhn-Tucker Conditions for Constrained Optimisation
- Quadratic Programming
- Separable Programming
- NLP Models with Solver
11 Introduction to game theory and its Applications
- Important terms in Game Theory
- Saddle points
- Mixed strategies: Games without saddle points
- 2 x n games
- Exploiting an opponent’s mistakes
12 Monte Carlo Simulation
- Reasons for using simulation
- Monte Carlo simulation
- Limitations of simulation
- Steps in the simulation process
- Some practical applications of simulation
- Two typical examples of hand-computed simulation
- Computer simulation
13 Queueing Models
- Characteristics of a queueing model
- Notations and Symbols
- Statistical methods in queueing
- The M/M/I System
- The M/M/C System
- The M/Ek/I System
- Decision problems in queueing
Assignment Problems
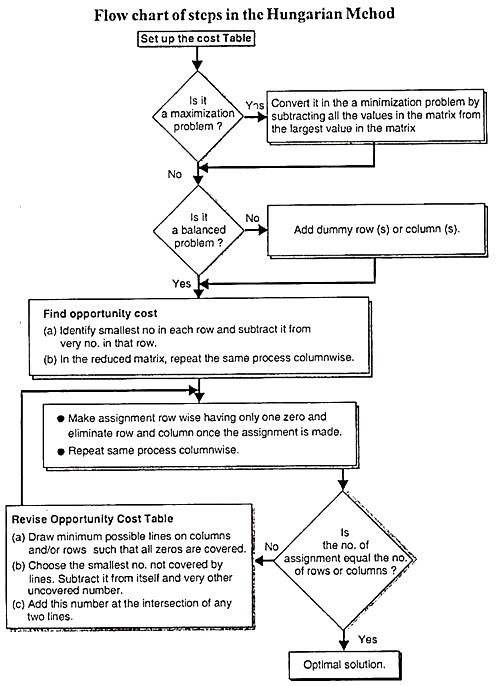
Definition of the assignment problem, mathematical formulation of the assignment problem, hungarian method for solving assignment problem, flow chart of hungarian method.
An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation.
The problem of assignment arises because available resources such as men, machines etc. have varying degrees of efficiency for performing different activities, therefore, cost, profit or loss of performing the different activities is different.
Thus, the problem is “How should the assignments be made so as to optimize the given objective”. Some of the problem where the assignment technique may be useful are assignment of workers to machines, salesman to different sales areas.
Suppose there are \(n\) jobs to be performed and \(n\) persons are available for doing these jobs. Assume that each person can do each job at a term, though with varying degree of efficiency, let \(c_{ij}\) be the cost if the \(i-th\) person is assigned to the \(j-th\) job. The problem is to find an assignment (which job should be assigned to which person one on-one basis) So that the total cost of performing all jobs is minimum, problem of this kind are known as assignment problem.
An assignment problem can be mathematically formulated as follows:
Minimise the total cost
\(x_{ij} =1\), if \(i^{th}\) person is assigned to the \(j^{th}\) job \(x_{ij}=0\), if \(i^{th}\) person is that assigned to the \(j^{th}\) job
subject to the constraints
i) \(\sum_{i=1}^n x_{ij} = 1, j=1, 2, \cdots n\)
which means that only one job is done by the \(i^{th}\) person, \(i= 1, 2, \cdots, n\)
ii) \(\sum_{i=1}^n x_{ij} = 1, j=1, 2, \cdots n\)
which means that only one person should be assigned to the \(j^{th}\) person, \(j= 1, 2, \cdots, n\)
The Hungarian method of assignment provides us with an efficient method of finding the optimal solution without having to make a-direct comparison of every solution. It works on the principle of reducing the given cost matrix to a matrix of opportunity costs.
Opportunity cost show the relative penalties associated with assigning resources to an activity as opposed to making the best or least cost assignment. If we can reduce the cost matrix to the extent of having at least one zero in each row and column, it will be possible to make optimal assignment.
The Hungarian method can be summarized in the following steps:
Step 1: Develop the Cost Table from the given Problem
If the no of rows are not equal to the no of columns and vice versa, a dummy row or dummy column must be added. The assignment cost for dummy cells are always zero.
Step 2: Find the Opportunity Cost Table
(a) Locate the smallest element in each row of the given cost table and then subtract that from each element of that row, and
(b) In the reduced matrix obtained from 2 (a) locate the smallest element in each column and then subtract that from each element. Each row and column now have at least one zero value.
Step 3: Make Assignment in the Opportunity Cost Matrix
The procedure of making assignment is as follows:
(a) Examine rows successively until a row with exactly one unmarked zero is obtained. Make an assignment single zero by making a square around it.
(b) For each zero value that becomes assigned, eliminate (Strike off) all other zeros in the same row and/ or column
(c) Repeat step 3 (a) and 3 (b) for each column also with exactly single zero value all that has not been assigned.
(d) If a row and/or column has two or more unmarked zeros and one cannot be chosen by inspection, then choose the assigned zero cell arbitrarily.
(e) Continue this process until all zeros in row column are either enclosed (Assigned) or struck off (x)
Step 4: Optimality Criterion
If the member of assigned cells is equal to the numbers of rows column then it is optimal solution. The total cost associated with this solution is obtained by adding original cost figures in the occupied cells.
If a zero cell was chosen arbitrarily in step (3), there exists an alternative optimal solution. But if no optimal solution is found, then go to step (5).
Step 5: Revise the Opportunity Cost Table
Draw a set of horizontal and vertical lines to cover all the zeros in the revised cost table obtained from step (3), by using the following procedure:
(a) For each row in which no assignment was made, mark a tick (√)
(b) Examine the marked rows. If any zero occurs in those columns, tick the respective rows that contain those assigned zeros.
(c) Repeat this process until no more rows or columns can be marked.
If a no of lines drawn is equal to the no of (or columns) the current solution is the optimal solution, otherwise go to step 6.
Step 6: Develop the New Revised Opportunity Cost Table
(a) From among the cells not covered by any line, choose the smallest element, call this value K
(b) Subtract K from every element in the cell not covered by line.
(c) Add K to very element in the cell covered by the two lines, i.e., intersection of two lines.
(d) Elements in cells covered by one line remain unchanged.
Step 7: Repeat Step 3 to 6 Unlit an Optimal Solution is Obtained
The flow chart of steps in the Hungarian method for solving an assignment problem is shown in following figures:
| 1) $$\begin{array}{ | c | c | c | c | c | c | } \hline {} & {M_1} & {M_2} & {M_3} & {M_4} & {M_5} \ \hline {O_1} & {24} & {29} & {18} & {32} & {19} \ \hline {O_2} & {17} & {26} & {34} & {22} & {21} \ \hline {O_3} & {27} & {16} & {28} & {17} & {25} \ \hline {O_4} & {22} & {18} & {28} & {30} & {24} \ \hline {O_5} & {28} & {16} & {31} & {24} & {27} \ \hline \end{array}$$ |
In a factory there are five operator \(O_1\), \(O_2\), \(O_3\), \(O_4\), \(O_5\) and five machine \(M_1\), \(M_2\), \(M_3\), \(M_4\), \(M_5\). The operating costs are given when the \(O_i\) operator operates the \(M_j\) machine \((i,j=1,2,..,5)\). But there is a restriction that \(O_3\) cannot be allowed to operate the third machine \(M_3\) and \(O_2\) cannot be allowed to operate the fifth machine \(M_5\). The cost matrix is given above. Find the optional assignment and the optimal assignment cost also.
[2018, 15M]
2) Solve the following assignment problem to maximize the sales: \(\begin{array}{|c|c|c|c|c|c|} \hline {} & {I} & {II} & {III} & {IV} & {V} \\ \hline {A} & {3} & {4} & {5} & {6} & {7} \\ \hline {B} & {4} & {15} & {13} & {7} & {6} \\ \hline {C} & {6} & {13} & {12} & {5} & {11} \\ \hline {D} & {7} & {12} & {15} & {8} & {5} \\ \hline {E} & {8} & {13} & {10} & {6} & {9} \\ \hline \end{array}\)
where \(I\), \(II\), \(III\), \(IV\) and \(V\) are Territories; \(A\), \(B\), \(C\), \(D\), \(E\) are Salesmen.
[2015, 10M]
3) Solve the minimum time assignment problem: \(\begin{array}{|c|c|c|c|c|} \hline { } & {I} & {II} & {III} & {IV} \\ \hline {A} & {3} & {12} & {5} & {4} \\ \hline {B} & {7} & {9} & {8} & {12} \\ \hline {C} & {5} & {11} & {10} & {12} \\ \hline {D} & {6} & {14} & {4} & {11} \\ \hline \end{array}\)
where \(I\), \(II\), \(III\) and \(IV\) are Machines; \(A\), \(B\), \(C\) and \(D\) are Jobs.
[2013, 15M]
4) A travelling salesman has to visit 5 cities. He wishes to start from a particular city, visit each city once and then return to his starting point. Cost of going from one city to another is given below:
You are required to find the least cost route.
[2004, 15M]
5) Find the optimal solution for the assignment problem with the following cost matrix: \(\begin{bmatrix}{6} & {1} & {9} & {11} & {12} \\ {2} & {8} & {17} & {2} & {5} \\ {11} & {8} & {3} & {3} & {3} \\ {4} & {10} & {8} & {6} & {11} \\ {8} & {10} & {11} & {5} & {13}\end{bmatrix}\)
Indicate clearly the rule you apply to arrive at the complete assignment.
[2003, 15M]
LIVE Course for free
- Ask a Question

An optimal solution of an assignment problem can be obtained only if, _________ (a) each row and column has only one zero element
An optimal solution of an assignment problem can be obtained only if, _________
(a) each row and column has only one zero element
(b) each row and column has at least one zero element
(c) The data is arranged in a square matrix
(d) None of the above
- operations research
Please log in or register to add a comment.
Please log in or register to answer this question..
Find MCQs & Mock Test
- JEE Main 2025 Test Series
- NEET Test Series
- Class 12 Chapterwise MCQ Test
- Class 11 Chapterwise Practice Test
- Class 10 Chapterwise MCQ Test
- Class 9 Chapterwise MCQ Test
- Class 8 Chapterwise MCQ Test
- Class 7 Chapterwise MCQ Test
Related questions
Welcome to Sarthaks eConnect: A unique platform where students can interact with teachers/experts/students to get solutions to their queries. Students (upto class 10+2) preparing for All Government Exams, CBSE Board Exam , ICSE Board Exam , State Board Exam, JEE (Mains+Advance) and NEET can ask questions from any subject and get quick answers by subject teachers/ experts/mentors/students.
- All categories
- JEE (36.7k)
- NEET (9.4k)
- Science (786k)
- Mathematics (256k)
- Statistics (3.0k)
- Environmental Science (5.4k)
- Biotechnology (704)
- Social Science (126k)
- Commerce (75.0k)
- Electronics (3.9k)
- Computer (21.9k)
- Artificial Intelligence (AI) (3.3k)
- Information Technology (21.8k)
- Programming (13.1k)
- Political Science (10.6k)
- Home Science (8.1k)
- Psychology (4.4k)
- Sociology (7.1k)
- English (68.2k)
- Hindi (30.8k)
- Aptitude (23.7k)
- Reasoning (14.8k)
- Olympiad (535)
- Skill Tips (91)
- RBSE (49.1k)
- General (73.2k)
- MSBSHSE (1.8k)
- Mathematics (1.5k)
- Physics (1.9k)
- Chemistry (4.3k)
- Bio Botany (1.3k)
- Bio Zoology (1.4k)
- English (867)
- Commerce (1.0k)
- Economics (1.5k)
- Accountancy (812)
- Computer Science (1.2k)
- Computer Applications (1.7k)
- Applications of Matrices and Determinants (89)
- Integral Calculus I (146)
- Integral Calculus II (94)
- Differential Equations (104)
- Numerical Methods (61)
- Random Variable and Mathematical Expectation (88)
- Probability Distributions (104)
- Sampling Techniques and Statistical Inference (81)
- Applied Statistics (126)
- Operations Research (72)
- Class 11 (18.6k)
- Class 10 (6.1k)
- Class 9 (3.7k)
- Class 8 (4.4k)
- Class 7 (4.2k)
- Class 6 (3.8k)
- Kerala Board (24.5k)
- Send feedback
- Privacy Policy
- Terms of Use
- Refund Policy
Quadratic assignment problem
Author: Thomas Kueny, Eric Miller, Natasha Rice, Joseph Szczerba, David Wittmann (SysEn 5800 Fall 2020)
- 1 Introduction
- 2.1 Koopmans-Beckman Mathematical Formulation
- 2.2.1 Parameters
- 2.3.1 Optimization Problem
- 2.4 Computational Complexity
- 2.5 Algorithmic Discussions
- 2.6 Branch and Bound Procedures
- 2.7 Linearizations
- 3.1 QAP with 3 Facilities
- 4.1 Inter-plant Transportation Problem
- 4.2 The Backboard Wiring Problem
- 4.3 Hospital Layout
- 4.4 Exam Scheduling System
- 5 Conclusion
- 6 References
Introduction
The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957 [1] , is a mathematical optimization module created to describe the location of invisible economic activities. An NP-Complete problem, this model can be applied to many other optimization problems outside of the field of economics. It has been used to optimize backboards, inter-plant transportation, hospital transportation, exam scheduling, along with many other applications not described within this page.
Theory, Methodology, and/or Algorithmic Discussions
Koopmans-beckman mathematical formulation.
Economists Koopmans and Beckman began their investigation of the QAP to ascertain the optimal method of locating important economic resources in a given area. The Koopmans-Beckman formulation of the QAP aims to achieve the objective of assigning facilities to locations in order to minimize the overall cost. Below is the Koopmans-Beckman formulation of the QAP as described by neos-guide.org.

Quadratic Assignment Problem Formulation

Inner Product

Note: The true objective cost function only requires summing entries above the diagonal in the matrix comprised of elements

Since this matrix is symmetric with zeroes on the diagonal, dividing by 2 removes the double count of each element to give the correct cost value. See the Numerical Example section for an example of this note.
Optimization Problem
With all of this information, the QAP can be summarized as:

Computational Complexity
QAP belongs to the classification of problems known as NP-complete, thus being a computationally complex problem. QAP’s NP-completeness was proven by Sahni and Gonzalez in 1976, who states that of all combinatorial optimization problems, QAP is the “hardest of the hard”. [2]
Algorithmic Discussions
While an algorithm that can solve QAP in polynomial time is unlikely to exist, there are three primary methods for acquiring the optimal solution to a QAP problem:
- Dynamic Program
- Cutting Plane
Branch and Bound Procedures
The third method has been proven to be the most effective in solving QAP, although when n > 15, QAP begins to become virtually unsolvable.
The Branch and Bound method was first proposed by Ailsa Land and Alison Doig in 1960 and is the most commonly used tool for solving NP-hard optimization problems.
A branch-and-bound algorithm consists of a systematic enumeration of candidate solutions by means of state space search: the set of candidate solutions is thought of as forming a rooted tree with the full set at the root. The algorithm explores branches of this tree, which represent subsets of the solution set. Before one lists all of the candidate solutions of a branch, the branch is checked against upper and lower estimated bounds on the optimal solution, and the branch is eliminated if it cannot produce a better solution than the best one found so far by the algorithm.
Linearizations
The first attempts to solve the QAP eliminated the quadratic term in the objective function of

in order to transform the problem into a (mixed) 0-1 linear program. The objective function is usually linearized by introducing new variables and new linear (and binary) constraints. Then existing methods for (mixed) linear integer programming (MILP) can be applied. The very large number of new variables and constraints, however, usually poses an obstacle for efficiently solving the resulting linear integer programs. MILP formulations provide LP relaxations of the problem which can be used to compute lower bounds.
Numerical Example
Qap with 3 facilities.

| Permutation | Cost |
| (123) | 91.4 |
| 99.8 | |
| 98.4 | |
| 86.5 | |
| 103.3 | |
| 90 |

Applications
Inter-plant transportation problem.
The QAP was first introduced by Koopmans and Beckmann to address how economic decisions could be made to optimize the transportation costs of goods between both manufacturing plants and locations. [1] Factoring in the location of each of the manufacturing plants as well as the volume of goods between locations to maximize revenue is what distinguishes this from other linear programming assignment problems like the Knapsack Problem.
The Backboard Wiring Problem
As the QAP is focused on minimizing the cost of traveling from one location to another, it is an ideal approach to determining the placement of components in many modern electronics. Leon Steinberg proposed a QAP solution to optimize the layout of elements on a blackboard by minimizing the total amount of wiring required. [4]
When defining the problem Steinberg states that we have a set of n elements

as well as a set of r points

In his paper he derives the below formula:

In his paper Steinberg a backboard with a 9 by 4 array, allowing for 36 potential positions for the 34 components that needed to be placed on the backboard. For the calculation, he selected a random initial placement of s1 and chose a random family of 25 unconnected sets.
The initial placement of components is shown below:

After the initial placement of elements, it took an additional 35 iterations to get us to our final optimized backboard layout. Leading to a total of 59 iterations and a final wire length of 4,969.440.
Hospital Layout
Building new hospitals was a common event in 1977 when Alealid N Elshafei wrote his paper on "Hospital Layouts as a Quadratic Assignment Problem". [5] With the high initial cost to construct the hospital and to staff it, it is important to ensure that it is operating as efficiently as possible. Elshafei's paper was commissioned to create an optimization formula to locate clinics within a building in such a way that minimizes the total distance that a patient travels within the hospital throughout the year. When doing a study of a major hospital in Cairo he determined that the Outpatient ward was acting as a bottleneck in the hospital and focused his efforts on optimizing the 17 departments there.
Elshafei identified the following QAP to determine where clinics should be placed:

For the Cairo hospital with 17 clinics, and one receiving and recording room bringing us to a total of 18 facilities. By running the above optimization Elshafei was able to get the total distance per year down to 11,281,887 from a distance of 13,973,298 based on the original hospital layout.
Exam Scheduling System
The scheduling system uses matrices for Exams, Time Slots, and Rooms with the goal of reducing the rate of schedule conflicts. To accomplish this goal, the “examination with the highest cross faculty student is been prioritized in the schedule after which the examination with the highest number of cross-program is considered and finally with the highest number of repeating student, at each stage group with the highest number of student are prioritized.” [6]

- ↑ 1.0 1.1 1.2 Koopmans, T., & Beckmann, M. (1957). Assignment Problems and the Location of Economic Activities. Econometrica, 25(1), 53-76. doi:10.2307/1907742
- ↑ 2.0 2.1 Quadratic Assignment Problem. (2020). Retrieved December 14, 2020, from https://neos-guide.org/content/quadratic-assignment-problem
- ↑ 3.0 3.1 3.2 Burkard, R. E., Çela, E., Pardalos, P. M., & Pitsoulis, L. S. (2013). The Quadratic Assignment Problem. https://www.opt.math.tugraz.at/~cela/papers/qap_bericht.pdf .
- ↑ 4.0 4.1 Leon Steinberg. The Backboard Wiring Problem: A Placement Algorithm. SIAM Review . 1961;3(1):37.
- ↑ 5.0 5.1 Alwalid N. Elshafei. Hospital Layout as a Quadratic Assignment Problem. Operational Research Quarterly (1970-1977) . 1977;28(1):167. doi:10.2307/300878
- ↑ 6.0 6.1 Muktar, D., & Ahmad, Z.M. (2014). Examination Scheduling System Based On Quadratic Assignment.
Navigation menu
Nash Balanced Assignment Problem
- Conference paper
- First Online: 21 November 2022
- Cite this conference paper

- Minh Hieu Nguyen 11 ,
- Mourad Baiou 11 &
- Viet Hung Nguyen 11
Part of the book series: Lecture Notes in Computer Science ((LNCS,volume 13526))
Included in the following conference series:
- International Symposium on Combinatorial Optimization
386 Accesses
2 Citations
In this paper, we consider a variant of the classic Assignment Problem (AP), called the Balanced Assignment Problem (BAP) [ 2 ]. The BAP seeks to find an assignment solution which has the smallest value of max-min distance : the difference between the maximum assignment cost and the minimum one. However, by minimizing only the max-min distance, the total cost of the BAP solution is neglected and it may lead to an inefficient solution in terms of total cost. Hence, we propose a fair way based on Nash equilibrium [ 1 , 3 , 4 ] to inject the total cost into the objective function of the BAP for finding assignment solutions having a better trade-off between the two objectives: the first aims at minimizing the total cost and the second aims at minimizing the max-min distance. For this purpose, we introduce the concept of Nash Fairness (NF) solutions based on the definition of proportional-fair scheduling adapted in the context of the AP: a transfer of utilities between the total cost and the max-min distance is considered to be fair if the percentage increase in the total cost is smaller than the percentage decrease in the max-min distance and vice versa.
We first show the existence of a NF solution for the AP which is exactly the optimal solution minimizing the product of the total cost and the max-min distance. However, finding such a solution may be difficult as it requires to minimize a concave function. The main result of this paper is to show that finding all NF solutions can be done in polynomial time. For that, we propose a Newton-based iterative algorithm converging to NF solutions in polynomial time. It consists in optimizing a sequence of linear combinations of the two objective based on Weighted Sum Method [ 5 ]. Computational results on various instances of the AP are presented and commented.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Subscribe and save.
- Get 10 units per month
- Download Article/Chapter or eBook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
- Available as PDF
- Read on any device
- Instant download
- Own it forever
- Available as EPUB and PDF
- Compact, lightweight edition
- Dispatched in 3 to 5 business days
- Free shipping worldwide - see info
Tax calculation will be finalised at checkout
Purchases are for personal use only
Institutional subscriptions
Similar content being viewed by others
The fair owa one-to-one assignment problem: np-hardness and polynomial time special cases.

An Efficient Primal-Dual Algorithm for Fair Combinatorial Optimization Problems
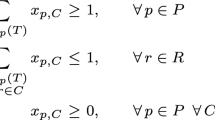
Restricted Max-Min Allocation: Integrality Gap and Approximation Algorithm
Bertsimas, D., Farias, V.F., Trichakis, N.: The price of fairness. Oper. Res. January–February 59 (1), 17–31 (2011)
MathSciNet MATH Google Scholar
Martello, S., Pulleyblank, W.R., Toth, P., De Werra, D.: Balanced optimization problems. Oper. Res. Lett. 3 (5), 275–278 (1984)
Article MathSciNet MATH Google Scholar
Kelly, F.P., Maullo, A.K., Tan, D.K.H.: Rate control for communication networks: shadow prices, proportional fairness and stability. J. Oper. Res. Soc. 49 (3), 237–252 (1997). https://doi.org/10.1057/palgrave.jors.2600523
Article Google Scholar
Ogryczak, W., Luss, H., Pioro, M., Nace, D., Tomaszewski, A.: Fair optimization and networks: a survey. J. Appl. Math. 2014 , 1–26 (2014)
Marler, R.T., Arora, J.S.: The weighted sum method for multi-objective optimization: new insights. Struct. Multi. Optim. 41 (6), 853–862 (2010)
Heller, I., Tompkins, C.B.: An extension of a theorem of Dantzig’s. Ann. Math. Stud. (38), 247–254 (1956)
Google Scholar
Kuhn, H.W.: The Hungarian method for assignment problem. Naval Res. Logist. Q. 2 (1–2), 83–97 (1955)
Martello, S.: Most and least uniform spanning trees. Discrete Appl. Math. 15 (2), 181–197 (1986)
Beasley, J.E.: Linear programming on Clay supercomputer. J. Oper. Res. Soc. 41 , 133–139 (1990)
Nguyen, M.H, Baiou, M., Nguyen, V.H., Vo, T.Q.T.: Nash fairness solutions for balanced TSP. In: International Network Optimization Conference (INOC2022) (2022)
Download references
Author information
Authors and affiliations.
INP Clermont Auvergne, Univ Clermont Auvergne, Mines Saint-Etienne, CNRS, UMR 6158 LIMOS, 1 Rue de la Chebarde, Aubiere Cedex, France
Minh Hieu Nguyen, Mourad Baiou & Viet Hung Nguyen
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Viet Hung Nguyen .
Editor information
Editors and affiliations.
ESSEC Business School of Paris, Cergy Pontoise Cedex, France
Ivana Ljubić
IBM TJ Watson Research Center, Yorktown Heights, NY, USA
Francisco Barahona
Georgia Institute of Technology, Atlanta, GA, USA
Santanu S. Dey
Université Paris-Dauphine, Paris, France
A. Ridha Mahjoub
Proposition 1 . There may be more than one NF solution for the AP.
Let us illustrate this by an instance of the AP having the following cost matrix
By verifying all feasible assignment solutions in this instance, we obtain easily three assignment solutions \((1-1, 2-2, 3-3), (1-2, 2-3, 3-1)\) , \((1-3, 2-2, 3-1)\) and \((1-3, 2-1, 3-2)\) corresponding to 4 NF solutions (280, 36), (320, 32), (340, 30) and (364, 28). Note that \(i-j\) where \(1 \le i,j \le 3\) represents the assignment between worker i and job j in the solution of this instance. \(\square \)
We recall below the proofs of some recent results that we have published in [ 10 ]. They are needed to prove the new results presented in this paper.
Theorem 2 [ 10 ] . \((P^{*},Q^{*}) = {{\,\mathrm{arg\,min}\,}}_{(P,Q) \in \mathcal {S}} PQ\) is a NF solution.
Obviously, there always exists a solution \((P^{*},Q^{*}) \in \mathcal {S}\) such that
Now \(\forall (P',Q') \in \mathcal {S}\) we have \(P'Q' \ge P^{*}Q^{*}\) . Then
The first inequality holds by the Cauchy-Schwarz inequality.
Hence, \((P^{*},Q^{*})\) is a NF solution. \(\square \)
Theorem 3 [ 10 ] . \((P^{*},Q^{*}) \in \mathcal {S}\) is a NF solution if and only if \((P^{*},Q^{*})\) is an optimal solution of \(\mathcal {P(\alpha ^{*})}\) where \(\alpha ^{*} = \frac{Q^{*}}{P^{*}}\) .
Firstly, let \((P^{*},Q^{*})\) be a NF solution and \(\alpha ^{*} = \frac{Q^{*}}{P^{*}}\) . We will show that \((P^{*},Q^{*})\) is an optimal solution of \(\mathcal {P(\alpha ^{*})}\) .
Since \((P^{*},Q^{*})\) is a NF solution, we have
Since \(\alpha ^{*} = \frac{Q^{*}}{P^{*}}\) , we have \(\alpha ^{*}P^{*}+Q^{*} = 2Q^{*}\) .
Dividing two sides of ( 6 ) by \(P^{*} > 0\) we obtain
So we deduce from ( 7 )
Hence, \((P^{*},Q^{*})\) is an optimal solution of \(\mathcal {P}(\alpha ^{*})\) .
Now suppose \(\alpha ^{*} = \frac{Q^{*}}{P^{*}}\) and \((P^{*},Q^{*})\) is an optimal solution of \(\mathcal {P}(\alpha ^{*})\) , we show that \((P^{*},Q^{*})\) is a NF solution.
If \((P^{*},Q^{*})\) is not a NF solution, there exists a solution \((P',Q') \in \mathcal {S}\) such that
We have then
which contradicts the optimality of \((P^{*},Q^{*})\) . \(\square \)
Lemma 3 [ 10 ] . Let \(\alpha , \alpha ' \in \mathbb {R}_+\) and \((P_{\alpha }, Q_{\alpha })\) , \((P_{\alpha '}, Q_{\alpha '})\) be the optimal solutions of \(\mathcal {P(\alpha )}\) and \(\mathcal {P(\alpha ')}\) respectively, if \(\alpha \le \alpha '\) then \(P_{\alpha } \ge P_{\alpha '}\) and \(Q_{\alpha } \le Q_{\alpha '}\) .
The optimality of \((P_{\alpha }, Q_{\alpha })\) and \((P_{\alpha '}, Q_{\alpha '})\) gives
By adding both sides of ( 8a ) and ( 8b ), we obtain \((\alpha - \alpha ') (P_{\alpha } - P_{\alpha '}) \le 0\) . Since \(\alpha \le \alpha '\) , it follows that \(P_{\alpha } \ge P_{\alpha '}\) .
On the other hand, inequality ( 8a ) implies \(Q_{\alpha '} - Q_{\alpha } \ge \alpha (P_{\alpha } - P_{\alpha '}) \ge 0\) that leads to \(Q_{\alpha } \le Q_{\alpha '}\) . \(\square \)
Lemma 4 [ 10 ] . During the execution of Procedure Find ( \(\alpha _{0})\) in Algorithm 1 , \(\alpha _{i} \in [0,1], \, \forall i \ge 1\) . Moreover, if \(T_{0} \ge 0\) then the sequence \(\{\alpha _i\}\) is non-increasing and \(T_{i} \ge 0, \, \forall i \ge 0\) . Otherwise, if \(T_{0} \le 0\) then the sequence \(\{\alpha _i\}\) is non-decreasing and \(T_{i} \le 0, \, \forall i \ge 0\) .
Since \(P \ge Q \ge 0, \, \forall (P, Q) \in \mathcal {S}\) , it follows that \(\alpha _{i+1} = \frac{Q_i}{P_i} \in [0,1], \, \forall i \ge 0\) .
We first consider \(T_{0} \ge 0\) . We proof \(\alpha _i \ge \alpha _{i+1}, \, \forall i \ge 0\) by induction on i . For \(i = 0\) , we have \(T_{0} = \alpha _{0} P_{0} - Q_{0} = P_{0}(\alpha _{0}-\alpha _{1}) \ge 0\) , it follows that \(\alpha _{0} \ge \alpha _{1}\) . Suppose that our hypothesis is true until \(i = k \ge 0\) , we will prove that it is also true with \(i = k+1\) .
Indeed, we have
The inductive hypothesis gives \(\alpha _k \ge \alpha _{k+1}\) that implies \(P_{k+1} \ge P_k > 0\) and \(Q_{k} \ge Q_{k+1} \ge 0\) according to Lemma 3 . It leads to \(Q_{k}P_{k+1} - P_{k}Q_{k+1} \ge 0\) and then \(\alpha _{k+1} - \alpha _{k+2} \ge 0\) .
Hence, we have \(\alpha _{i} \ge \alpha _{i+1}, \, \forall i \ge 0\) .
Consequently, \(T_{i} = \alpha _{i}P_{i} - Q_{i} = P_{i}(\alpha _{i}-\alpha _{i+1}) \ge 0, \, \forall i \ge 0\) .
Similarly, if \(T_{0} \le 0\) we obtain that the sequence \(\{\alpha _i\}\) is non-decreasing and \(T_{i} \le 0, \, \forall i \ge 0\) . That concludes the proof. \(\square \)
Lemma 5 [ 10 ] . From each \(\alpha _{0} \in [0,1]\) , Procedure Find \((\alpha _{0})\) converges to a coefficient \(\alpha _{k} \in \mathcal {C}_{0}\) satisfying \(\alpha _{k}\) is the unique element \(\in \mathcal {C}_{0}\) between \(\alpha _{0}\) and \(\alpha _{k}\) .
As a consequence of Lemma 4 , Procedure \(\textit{Find}(\alpha _{0})\) converges to a coefficient \(\alpha _{k} \in [0,1], \forall \alpha _{0} \in [0,1]\) .
By the stopping criteria of Procedure Find \((\alpha _{0})\) , when \(T_{k} = \alpha _{k} P_{k} - Q_{k} = 0\) we obtain \(\alpha _{k} \in C_{0}\) and \((P_{k},Q_{k})\) is a NF solution. (Theorem 3 )
If \(T_{0} = 0\) then obviously \(\alpha _{k} = \alpha _{0}\) . We consider \(T_{0} > 0\) and the sequence \(\{\alpha _i\}\) is now non-negative, non-increasing. We will show that \([\alpha _{k},\alpha _{0}] \cap \mathcal {C}_{0} = \alpha _{k}\) .
Suppose that we have \(\alpha \in (\alpha _{k},\alpha _{0}]\) and \(\alpha \in \mathcal {C}_{0}\) corresponding to a NF solution ( P , Q ). Then there exists \(1 \le i \le k\) such that \(\alpha \in (\alpha _{i}, \alpha _{i-1}]\) . Since \(\alpha \le \alpha _{i-1}\) , \(P \ge P_{i-1}\) and \(Q \le Q_{i-1}\) due to Lemma 3 . Thus, we get
By the definitions of \(\alpha \) and \(\alpha _{i}\) , inequality ( 9 ) is equivalent to \(\alpha \le \alpha _{i}\) which leads to a contradiction.
By repeating the same argument for \(T_{0} < 0\) , we also have a contradiction. \(\square \)
Rights and permissions
Reprints and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper.
Nguyen, M.H., Baiou, M., Nguyen, V.H. (2022). Nash Balanced Assignment Problem. In: Ljubić, I., Barahona, F., Dey, S.S., Mahjoub, A.R. (eds) Combinatorial Optimization. ISCO 2022. Lecture Notes in Computer Science, vol 13526. Springer, Cham. https://doi.org/10.1007/978-3-031-18530-4_13
Download citation
DOI : https://doi.org/10.1007/978-3-031-18530-4_13
Published : 21 November 2022
Publisher Name : Springer, Cham
Print ISBN : 978-3-031-18529-8
Online ISBN : 978-3-031-18530-4
eBook Packages : Computer Science Computer Science (R0)
Share this paper
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Publish with us
Policies and ethics
- Find a journal
- Track your research

IMAGES
COMMENTS
Exercise 17 shows that the number of iterations is O(n2). To compare the Hungarian method to the exhaustive search method mentioned above, suppose that each iteration can be performed in one second. Then an assignment prob-lem with n = 30 can be solved in at most 302 = 900 seconds, or 15 minutes of computer time.
The formal definition of the assignment problem (or linear assignment problem) is . Given two sets, A and T, together with a weight function C : A × T → R.Find a bijection f : A → T such that the cost function: (, ())is minimized. Usually the weight function is viewed as a square real-valued matrix C, so that the cost function is written down as: , The problem is "linear" because the cost ...
This question is answered in detail in section 5.3 of Assignment Problems (Burkard, Dell'Amico, Martello). Also see: Burkard & Butkovič (2003) "Max algebra and the linear assignment problem." Mathematical Programming 98, 415-429. Unfortunately, all of these results are approachable but difficult to concisely summarize (for me at least).
Connection Between Transportation and Assignment Problem An assignment problem is a special case of transportation problem in which m = n, all a i and b j are unity and each is limited to either 0 or 1. Hungarian Method for Solving an Assignment Problem 1. Prepare a square n n matrix. If not, make it square by adding suitable
Step 1: Set up the cost matrix. The first step in solving the assignment problem is to set up the cost matrix, which represents the cost of assigning a task to an agent. The matrix should be square and have the same number of rows and columns as the number of tasks and agents, respectively.
What an Assignment problem is? •When we want to solve a linear programming problem with special characteristic such as a Square Matrix (i.e. No. of destinations are same as no. of sources) ... equal to the order of the matrix; hence a optimal solution is obtained. Step 4 Making the optimal Assignment: a. Select the a row with only one '0 ...
a column of C, we will not change the optimal solu. ion.Observation 2. Consider an assignment problem with cost matrix C. If C 0, and there exists an assignmen. which only assigns i to j if cij = 0, then this assigment is optimal.These two observations give us an idea for an algorithm: we subtract the minimu.
Lemma 3. Let M' be matching obtained by augmenting along a min cost path with respect to c p+d. Then p' = p + d is compatible with M'. Pf.! By Lemma 2, the prices p + d are compatible for M.! Since we augment along a min cost path, the only edges (x, y) that swap into or out of the matching are on the shortest path.!
10 Feb 2019. Whenever the cost matrix of an assignment problem is not a square matrix, that is, whenever the number of sources is not equal to the number of destinations, the assignment problem is called an unbalanced assignment problem. In such problems, dummy rows (or columns) are added in the matrix so as to complete it to form a square matrix.
2.1.2 The Quadratic Assignment Problem As previously mentioned, the focus of this paper is more complicated general-ization of the linear assignment problem, known as the quadratic assignment problem. In addition to a cost matrix, as in the LAP above, there is also a so-called distance matrix involved. In order to preserve consistency, we will
the assignment matrix, the number of agents are not equal to the number of tasks. Such problems can be termed as unbalanced assignment problem. The effectiveness matrix in this case will not be a square matrix. In such problems, dummy row(s) or dummy column(s) are added in the matrix so as to complete it to form a square matrix.
2.1 Assignment problem is a variant form of transportation problem. The assignment problem is special case of the transportation problem with two characteristics. First, the pay off matrix for the problem would be square, and, second, the optimal solution to the problem would always
Clearly [Cij] is a square matrix of order n. L , Assignment Problem as a special case of Transportation Problem. Let us consider an m x n transportation problem: Minimise Z = x Ccij xg n I I xx, = a, (i = 1,2, +.. ... assignment problem, obtained after adding or subtracting constants ui's and vjls from its rows and colun~ns.
An assignment problem is a particular case of transportation problem where the objective is to assign a number of resources to an equal number of activities so as to minimise total cost or maximize total profit of allocation. ... In the reduced matrix obtained from 2 (a) locate the smallest element in each column and then subtract that from ...
An optimal solution of an assignment problem can be obtained only if, _____ (a) each row and column has only one zero element (b) each row and column has at least one zero element (c) The data is arranged in a square matrix (d) None of the above
Step 3. Draw lines through appropriate rows and columns so that all the zero entries of the cost matrix are covered and the minimum number of such lines is used. Step 4. Test for Optimality: (i) If the minimum number of covering lines is n, an optimal assignment of zeros is possible and we are finished.
the given cost matrix is not a square matrix, the assignment problem is called an unbalanced problem. In such cases a dummy persons(s) or jobs(s) are added in the matrix (with zeros as the cost ...
square matrix. Step 2 For each row in assignment problem, the maximum or minimum value(say ) from the row is picked depending upon the nature of the problem . And the chosen element (say ) is divided in each row resulting in a unity (1), at least once. Step 3 Each row is to be discussed Consider the 1‟s of (i , j)th position and consider the ...
Now, we introduce a new algorithm for finding optimal solution of an Assignment problem. The. step wise procedure of the proposed method is as follows: Step 1: Construct the Assignment table from ...
The Assignment Problem (Square Matrices) 1.1 Mathematical Statement Given the n N n matrix (a~j) of real numbers, find a ... The assignment problem can be extended to rec- ... Let (b~i) be a l X l matrix obtained by adding l - k lines of the same element a to the initial n X m matrix (a~i). The matrix (b~i) may be divided into two sub-
The Quadratic Assignment Problem (QAP), discovered by Koopmans and Beckmann in 1957 ... = is an n x n matrix where the required flow between facilities and . = is an n x n matrix where the distance between facilities and and . Intuitively, the product of distance and flow represents cost, and the objective is to minimize this cost. ...
The Assignment Problem (AP) is a fundamental combinatorial optimization problem. It can be formally defined as follows. Given a set n workers, a set of n jobs and a \(n \times n\) cost matrix whose elements are positive representing the assignment of any worker to any job, the AP aims at finding an one-to-one worker-job assignment (i.e., a bipartite perfect matching) that minimizes certain ...