Hungarian Method

The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives. In 1955, Harold Kuhn used the term “Hungarian method” to honour two Hungarian mathematicians, Dénes Kőnig and Jenő Egerváry. Let’s go through the steps of the Hungarian method with the help of a solved example.

Hungarian Method to Solve Assignment Problems
The Hungarian method is a simple way to solve assignment problems. Let us first discuss the assignment problems before moving on to learning the Hungarian method.
What is an Assignment Problem?
A transportation problem is a type of assignment problem. The goal is to allocate an equal amount of resources to the same number of activities. As a result, the overall cost of allocation is minimised or the total profit is maximised.
Because available resources such as workers, machines, and other resources have varying degrees of efficiency for executing different activities, and hence the cost, profit, or loss of conducting such activities varies.
Assume we have ‘n’ jobs to do on ‘m’ machines (i.e., one job to one machine). Our goal is to assign jobs to machines for the least amount of money possible (or maximum profit). Based on the notion that each machine can accomplish each task, but at variable levels of efficiency.
Hungarian Method Steps
Check to see if the number of rows and columns are equal; if they are, the assignment problem is considered to be balanced. Then go to step 1. If it is not balanced, it should be balanced before the algorithm is applied.
Step 1 – In the given cost matrix, subtract the least cost element of each row from all the entries in that row. Make sure that each row has at least one zero.
Step 2 – In the resultant cost matrix produced in step 1, subtract the least cost element in each column from all the components in that column, ensuring that each column contains at least one zero.
Step 3 – Assign zeros
- Analyse the rows one by one until you find a row with precisely one unmarked zero. Encircle this lonely unmarked zero and assign it a task. All other zeros in the column of this circular zero should be crossed out because they will not be used in any future assignments. Continue in this manner until you’ve gone through all of the rows.
- Examine the columns one by one until you find one with precisely one unmarked zero. Encircle this single unmarked zero and cross any other zero in its row to make an assignment to it. Continue until you’ve gone through all of the columns.
Step 4 – Perform the Optimal Test
- The present assignment is optimal if each row and column has exactly one encircled zero.
- The present assignment is not optimal if at least one row or column is missing an assignment (i.e., if at least one row or column is missing one encircled zero). Continue to step 5. Subtract the least cost element from all the entries in each column of the final cost matrix created in step 1 and ensure that each column has at least one zero.
Step 5 – Draw the least number of straight lines to cover all of the zeros as follows:
(a) Highlight the rows that aren’t assigned.
(b) Label the columns with zeros in marked rows (if they haven’t already been marked).
(c) Highlight the rows that have assignments in indicated columns (if they haven’t previously been marked).
(d) Continue with (b) and (c) until no further marking is needed.
(f) Simply draw the lines through all rows and columns that are not marked. If the number of these lines equals the order of the matrix, then the solution is optimal; otherwise, it is not.
Step 6 – Find the lowest cost factor that is not covered by the straight lines. Subtract this least-cost component from all the uncovered elements and add it to all the elements that are at the intersection of these straight lines, but leave the rest of the elements alone.
Step 7 – Continue with steps 1 – 6 until you’ve found the highest suitable assignment.
|
|
|---|
Hungarian Method Example
Use the Hungarian method to solve the given assignment problem stated in the table. The entries in the matrix represent each man’s processing time in hours.
\(\begin{array}{l}\begin{bmatrix} & I & II & III & IV & V \\1 & 20 & 15 & 18 & 20 & 25 \\2 & 18 & 20 & 12 & 14 & 15 \\3 & 21 & 23 & 25 & 27 & 25 \\4 & 17 & 18 & 21 & 23 & 20 \\5 & 18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)
With 5 jobs and 5 men, the stated problem is balanced.
\(\begin{array}{l}A = \begin{bmatrix}20 & 15 & 18 & 20 & 25 \\18 & 20 & 12 & 14 & 15 \\21 & 23 & 25 & 27 & 25 \\17 & 18 & 21 & 23 & 20 \\18 & 18 & 16 & 19 & 20 \\\end{bmatrix}\end{array} \)
Subtract the lowest cost element in each row from all of the elements in the given cost matrix’s row. Make sure that each row has at least one zero.
\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 5 & 10 \\6 & 8 & 0 & 2 & 3 \\0 & 2 & 4 & 6 & 4 \\0 & 1 & 4 & 6 & 3 \\2 & 2 & 0 & 3 & 4 \\\end{bmatrix}\end{array} \)
Subtract the least cost element in each Column from all of the components in the given cost matrix’s Column. Check to see if each column has at least one zero.
\(\begin{array}{l}A = \begin{bmatrix}5 & 0 & 3 & 3 & 7 \\6 & 8 & 0 & 0 & 0 \\0 & 2 & 4 & 4 & 1 \\0 & 1 & 4 & 4 & 0 \\2 & 2 & 0 & 1 & 1 \\\end{bmatrix}\end{array} \)
When the zeros are assigned, we get the following:
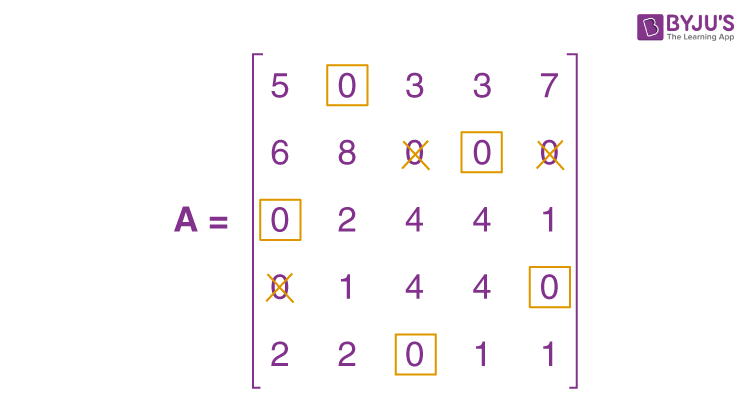
The present assignment is optimal because each row and column contain precisely one encircled zero.
Where 1 to II, 2 to IV, 3 to I, 4 to V, and 5 to III are the best assignments.
Hence, z = 15 + 14 + 21 + 20 + 16 = 86 hours is the optimal time.
Practice Question on Hungarian Method
Use the Hungarian method to solve the following assignment problem shown in table. The matrix entries represent the time it takes for each job to be processed by each machine in hours.
\(\begin{array}{l}\begin{bmatrix}J/M & I & II & III & IV & V \\1 & 9 & 22 & 58 & 11 & 19 \\2 & 43 & 78 & 72 & 50 & 63 \\3 & 41 & 28 & 91 & 37 & 45 \\4 & 74 & 42 & 27 & 49 & 39 \\5 & 36 & 11 & 57 & 22 & 25 \\\end{bmatrix}\end{array} \)
Stay tuned to BYJU’S – The Learning App and download the app to explore all Maths-related topics.
Frequently Asked Questions on Hungarian Method
What is hungarian method.
The Hungarian method is defined as a combinatorial optimization technique that solves the assignment problems in polynomial time and foreshadowed subsequent primal–dual approaches.
What are the steps involved in Hungarian method?
The following is a quick overview of the Hungarian method: Step 1: Subtract the row minima. Step 2: Subtract the column minimums. Step 3: Use a limited number of lines to cover all zeros. Step 4: Add some more zeros to the equation.
What is the purpose of the Hungarian method?
When workers are assigned to certain activities based on cost, the Hungarian method is beneficial for identifying minimum costs.
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.
- DSA Tutorial
- Data Structures
- Linked List
- Dynamic Programming
- Binary Tree
- Binary Search Tree
- Divide & Conquer
- Mathematical
- Backtracking
- Branch and Bound
- Pattern Searching
Hungarian Algorithm for Assignment Problem | Set 2 (Implementation)
Given a 2D array , arr of size N*N where arr[i][j] denotes the cost to complete the j th job by the i th worker. Any worker can be assigned to perform any job. The task is to assign the jobs such that exactly one worker can perform exactly one job in such a way that the total cost of the assignment is minimized.
Input: arr[][] = {{3, 5}, {10, 1}} Output: 4 Explanation: The optimal assignment is to assign job 1 to the 1st worker, job 2 to the 2nd worker. Hence, the optimal cost is 3 + 1 = 4. Input: arr[][] = {{2500, 4000, 3500}, {4000, 6000, 3500}, {2000, 4000, 2500}} Output: 4 Explanation: The optimal assignment is to assign job 2 to the 1st worker, job 3 to the 2nd worker and job 1 to the 3rd worker. Hence, the optimal cost is 4000 + 3500 + 2000 = 9500.
Different approaches to solve this problem are discussed in this article .
Approach: The idea is to use the Hungarian Algorithm to solve this problem. The algorithm is as follows:
- For each row of the matrix, find the smallest element and subtract it from every element in its row.
- Repeat the step 1 for all columns.
- Cover all zeros in the matrix using the minimum number of horizontal and vertical lines.
- Test for Optimality : If the minimum number of covering lines is N , an optimal assignment is possible. Else if lines are lesser than N , an optimal assignment is not found and must proceed to step 5.
- Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to step 3.
Consider an example to understand the approach:
Let the 2D array be: 2500 4000 3500 4000 6000 3500 2000 4000 2500 Step 1: Subtract minimum of every row. 2500, 3500 and 2000 are subtracted from rows 1, 2 and 3 respectively. 0 1500 1000 500 2500 0 0 2000 500 Step 2: Subtract minimum of every column. 0, 1500 and 0 are subtracted from columns 1, 2 and 3 respectively. 0 0 1000 500 1000 0 0 500 500 Step 3: Cover all zeroes with minimum number of horizontal and vertical lines. Step 4: Since we need 3 lines to cover all zeroes, the optimal assignment is found. 2500 4000 3500 4000 6000 3500 2000 4000 2500 So the optimal cost is 4000 + 3500 + 2000 = 9500
For implementing the above algorithm, the idea is to use the max_cost_assignment() function defined in the dlib library . This function is an implementation of the Hungarian algorithm (also known as the Kuhn-Munkres algorithm) which runs in O(N 3 ) time. It solves the optimal assignment problem.
Below is the implementation of the above approach:
Time Complexity: O(N 3 ) Auxiliary Space: O(N 2 )
Please Login to comment...
Similar reads.
- How to Get a Free SSL Certificate
- Best SSL Certificates Provider in India
- Elon Musk's xAI releases Grok-2 AI assistant
- What is OpenAI SearchGPT? How it works and How to Get it?
- Content Improvement League 2024: From Good To A Great Article
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
- Implementation of the Hungarian algorithm
- Connection to the Successive Shortest Path Algorithm
- Task examples
- Practice Problems
Hungarian algorithm for solving the assignment problem ¶
Statement of the assignment problem ¶.
There are several standard formulations of the assignment problem (all of which are essentially equivalent). Here are some of them:
There are $n$ jobs and $n$ workers. Each worker specifies the amount of money they expect for a particular job. Each worker can be assigned to only one job. The objective is to assign jobs to workers in a way that minimizes the total cost.
Given an $n \times n$ matrix $A$ , the task is to select one number from each row such that exactly one number is chosen from each column, and the sum of the selected numbers is minimized.
Given an $n \times n$ matrix $A$ , the task is to find a permutation $p$ of length $n$ such that the value $\sum A[i]\left[p[i]\right]$ is minimized.
Consider a complete bipartite graph with $n$ vertices per part, where each edge is assigned a weight. The objective is to find a perfect matching with the minimum total weight.
It is important to note that all the above scenarios are " square " problems, meaning both dimensions are always equal to $n$ . In practice, similar " rectangular " formulations are often encountered, where $n$ is not equal to $m$ , and the task is to select $\min(n,m)$ elements. However, it can be observed that a "rectangular" problem can always be transformed into a "square" problem by adding rows or columns with zero or infinite values, respectively.
We also note that by analogy with the search for a minimum solution, one can also pose the problem of finding a maximum solution. However, these two problems are equivalent to each other: it is enough to multiply all the weights by $-1$ .
Hungarian algorithm ¶
Historical reference ¶.
The algorithm was developed and published by Harold Kuhn in 1955. Kuhn himself gave it the name "Hungarian" because it was based on the earlier work by Hungarian mathematicians Dénes Kőnig and Jenő Egerváry. In 1957, James Munkres showed that this algorithm runs in (strictly) polynomial time, independently from the cost. Therefore, in literature, this algorithm is known not only as the "Hungarian", but also as the "Kuhn-Mankres algorithm" or "Mankres algorithm". However, it was recently discovered in 2006 that the same algorithm was invented a century before Kuhn by the German mathematician Carl Gustav Jacobi . His work, About the research of the order of a system of arbitrary ordinary differential equations , which was published posthumously in 1890, contained, among other findings, a polynomial algorithm for solving the assignment problem. Unfortunately, since the publication was in Latin, it went unnoticed among mathematicians.
It is also worth noting that Kuhn's original algorithm had an asymptotic complexity of $\mathcal{O}(n^4)$ , and only later Jack Edmonds and Richard Karp (and independently Tomizawa ) showed how to improve it to an asymptotic complexity of $\mathcal{O}(n^3)$ .
The $\mathcal{O}(n^4)$ algorithm ¶
To avoid ambiguity, we note right away that we are mainly concerned with the assignment problem in a matrix formulation (i.e., given a matrix $A$ , you need to select $n$ cells from it that are in different rows and columns). We index arrays starting with $1$ , i.e., for example, a matrix $A$ has indices $A[1 \dots n][1 \dots n]$ .
We will also assume that all numbers in matrix A are non-negative (if this is not the case, you can always make the matrix non-negative by adding some constant to all numbers).
Let's call a potential two arbitrary arrays of numbers $u[1 \ldots n]$ and $v[1 \ldots n]$ , such that the following condition is satisfied:
(As you can see, $u[i]$ corresponds to the $i$ -th row, and $v[j]$ corresponds to the $j$ -th column of the matrix).
Let's call the value $f$ of the potential the sum of its elements:
On one hand, it is easy to see that the cost of the desired solution $sol$ is not less than the value of any potential.
Lemma. $sol\geq f.$
The desired solution of the problem consists of $n$ cells of the matrix $A$ , so $u[i]+v[j]\leq A[i][j]$ for each of them. Since all the elements in $sol$ are in different rows and columns, summing these inequalities over all the selected $A[i][j]$ , you get $f$ on the left side of the inequality, and $sol$ on the right side.
On the other hand, it turns out that there is always a solution and a potential that turns this inequality into equality . The Hungarian algorithm described below will be a constructive proof of this fact. For now, let's just pay attention to the fact that if any solution has a cost equal to any potential, then this solution is optimal .
Let's fix some potential. Let's call an edge $(i,j)$ rigid if $u[i]+v[j]=A[i][j].$
Recall an alternative formulation of the assignment problem, using a bipartite graph. Denote with $H$ a bipartite graph composed only of rigid edges. The Hungarian algorithm will maintain, for the current potential, the maximum-number-of-edges matching $M$ of the graph $H$ . As soon as $M$ contains $n$ edges, then the solution to the problem will be just $M$ (after all, it will be a solution whose cost coincides with the value of a potential).
Let's proceed directly to the description of the algorithm .
Step 1. At the beginning, the potential is assumed to be zero ( $u[i]=v[i]=0$ for all $i$ ), and the matching $M$ is assumed to be empty.
Step 2. Further, at each step of the algorithm, we try, without changing the potential, to increase the cardinality of the current matching $M$ by one (recall that the matching is searched in the graph of rigid edges $H$ ). To do this, the usual Kuhn Algorithm for finding the maximum matching in bipartite graphs is used. Let us recall the algorithm here. All edges of the matching $M$ are oriented in the direction from the right part to the left one, and all other edges of the graph $H$ are oriented in the opposite direction.
Recall (from the terminology of searching for matchings) that a vertex is called saturated if an edge of the current matching is adjacent to it. A vertex that is not adjacent to any edge of the current matching is called unsaturated. A path of odd length, in which the first edge does not belong to the matching, and for all subsequent edges there is an alternating belonging to the matching (belongs/does not belong) - is called an augmenting path. From all unsaturated vertices in the left part, a depth-first or breadth-first traversal is started. If, as a result of the search, it was possible to reach an unsaturated vertex of the right part, we have found an augmenting path from the left part to the right one. If we include odd edges of the path and remove the even ones in the matching (i.e. include the first edge in the matching, exclude the second, include the third, etc.), then we will increase the matching cardinality by one.
If there was no augmenting path, then the current matching $M$ is maximal in the graph $H$ .
Step 3. If at the current step, it is not possible to increase the cardinality of the current matching, then a recalculation of the potential is performed in such a way that, at the next steps, there will be more opportunities to increase the matching.
Denote by $Z_1$ the set of vertices of the left part that were visited during the last traversal of Kuhn's algorithm, and through $Z_2$ the set of visited vertices of the right part.
Let's calculate the value $\Delta$ :
Lemma. $\Delta > 0.$
Suppose $\Delta=0$ . Then there exists a rigid edge $(i,j)$ with $i\in Z_1$ and $j\notin Z_2$ . It follows that the edge $(i,j)$ must be oriented from the right part to the left one, i.e. $(i,j)$ must be included in the matching $M$ . However, this is impossible, because we could not get to the saturated vertex $i$ except by going along the edge from j to i. So $\Delta > 0$ .
Now let's recalculate the potential in this way:
for all vertices $i\in Z_1$ , do $u[i] \gets u[i]+\Delta$ ,
for all vertices $j\in Z_2$ , do $v[j] \gets v[j]-\Delta$ .
Lemma. The resulting potential is still a correct potential.
We will show that, after recalculation, $u[i]+v[j]\leq A[i][j]$ for all $i,j$ . For all the elements of $A$ with $i\in Z_1$ and $j\in Z_2$ , the sum $u[i]+v[j]$ does not change, so the inequality remains true. For all the elements with $i\notin Z_1$ and $j\in Z_2$ , the sum $u[i]+v[j]$ decreases by $\Delta$ , so the inequality is still true. For the other elements whose $i\in Z_1$ and $j\notin Z_2$ , the sum increases, but the inequality is still preserved, since the value $\Delta$ is, by definition, the maximum increase that does not change the inequality.
Lemma. The old matching $M$ of rigid edges is valid, i.e. all edges of the matching will remain rigid.
For some rigid edge $(i,j)$ to stop being rigid as a result of a change in potential, it is necessary that equality $u[i] + v[j] = A[i][j]$ turns into inequality $u[i] + v[j] < A[i][j]$ . However, this can happen only when $i \notin Z_1$ and $j \in Z_2$ . But $i \notin Z_1$ implies that the edge $(i,j)$ could not be a matching edge.
Lemma. After each recalculation of the potential, the number of vertices reachable by the traversal, i.e. $|Z_1|+|Z_2|$ , strictly increases.
First, note that any vertex that was reachable before recalculation, is still reachable. Indeed, if some vertex is reachable, then there is some path from reachable vertices to it, starting from the unsaturated vertex of the left part; since for edges of the form $(i,j),\ i\in Z_1,\ j\in Z_2$ the sum $u[i]+v[j]$ does not change, this entire path will be preserved after changing the potential. Secondly, we show that after a recalculation, at least one new vertex will be reachable. This follows from the definition of $\Delta$ : the edge $(i,j)$ which $\Delta$ refers to will become rigid, so vertex $j$ will be reachable from vertex $i$ .
Due to the last lemma, no more than $n$ potential recalculations can occur before an augmenting path is found and the matching cardinality of $M$ is increased. Thus, sooner or later, a potential that corresponds to a perfect matching $M^*$ will be found, and $M^*$ will be the answer to the problem. If we talk about the complexity of the algorithm, then it is $\mathcal{O}(n^4)$ : in total there should be at most $n$ increases in matching, before each of which there are no more than $n$ potential recalculations, each of which is performed in time $\mathcal{O}(n^2)$ .
We will not give the implementation for the $\mathcal{O}(n^4)$ algorithm here, since it will turn out to be no shorter than the implementation for the $\mathcal{O}(n^3)$ one, described below.
The $\mathcal{O}(n^3)$ algorithm ¶
Now let's learn how to implement the same algorithm in $\mathcal{O}(n^3)$ (for rectangular problems $n \times m$ , $\mathcal{O}(n^2m)$ ).
The key idea is to consider matrix rows one by one , and not all at once. Thus, the algorithm described above will take the following form:
Consider the next row of the matrix $A$ .
While there is no increasing path starting in this row, recalculate the potential.
As soon as an augmenting path is found, propagate the matching along it (thus including the last edge in the matching), and restart from step 1 (to consider the next line).
To achieve the required complexity, it is necessary to implement steps 2-3, which are performed for each row of the matrix, in time $\mathcal{O}(n^2)$ (for rectangular problems in $\mathcal{O}(nm)$ ).
To do this, recall two facts proved above:
With a change in the potential, the vertices that were reachable by Kuhn's traversal will remain reachable.
In total, only $\mathcal{O}(n)$ recalculations of the potential could occur before an augmenting path was found.
From this follow these key ideas that allow us to achieve the required complexity:
To check for the presence of an augmenting path, there is no need to start the Kuhn traversal again after each potential recalculation. Instead, you can make the Kuhn traversal in an iterative form : after each recalculation of the potential, look at the added rigid edges and, if their left ends were reachable, mark their right ends reachable as well and continue the traversal from them.
Developing this idea further, we can present the algorithm as follows: at each step of the loop, the potential is recalculated. Subsequently, a column that has become reachable is identified (which will always exist as new reachable vertices emerge after every potential recalculation). If the column is unsaturated, an augmenting chain is discovered. Conversely, if the column is saturated, the matching row also becomes reachable.
To quickly recalculate the potential (faster than the $\mathcal{O}(n^2)$ naive version), you need to maintain auxiliary minima for each of the columns:
$minv[j]=\min_{i\in Z_1} A[i][j]-u[i]-v[j].$
It's easy to see that the desired value $\Delta$ is expressed in terms of them as follows:
$\Delta=\min_{j\notin Z_2} minv[j].$
Thus, finding $\Delta$ can now be done in $\mathcal{O}(n)$ .
It is necessary to update the array $minv$ when new visited rows appear. This can be done in $\mathcal{O}(n)$ for the added row (which adds up over all rows to $\mathcal{O}(n^2)$ ). It is also necessary to update the array $minv$ when recalculating the potential, which is also done in time $\mathcal{O}(n)$ ( $minv$ changes only for columns that have not yet been reached: namely, it decreases by $\Delta$ ).
Thus, the algorithm takes the following form: in the outer loop, we consider matrix rows one by one. Each row is processed in time $\mathcal{O}(n^2)$ , since only $\mathcal{O}(n)$ potential recalculations could occur (each in time $\mathcal{O}(n)$ ), and the array $minv$ is maintained in time $\mathcal{O}(n^2)$ ; Kuhn's algorithm will work in time $\mathcal{O}(n^2)$ (since it is presented in the form of $\mathcal{O}(n)$ iterations, each of which visits a new column).
The resulting complexity is $\mathcal{O}(n^3)$ or, if the problem is rectangular, $\mathcal{O}(n^2m)$ .
Implementation of the Hungarian algorithm ¶
The implementation below was developed by Andrey Lopatin several years ago. It is distinguished by amazing conciseness: the entire algorithm consists of 30 lines of code .
The implementation finds a solution for the rectangular matrix $A[1\dots n][1\dots m]$ , where $n\leq m$ . The matrix is 1-based for convenience and code brevity: this implementation introduces a dummy zero row and zero column, which allows us to write many cycles in a general form, without additional checks.
Arrays $u[0 \ldots n]$ and $v[0 \ldots m]$ store potential. Initially, they are set to zero, which is consistent with a matrix of zero rows (Note that it is unimportant for this implementation whether or not the matrix $A$ contains negative numbers).
The array $p[0 \ldots m]$ contains a matching: for each column $j = 1 \ldots m$ , it stores the number $p[j]$ of the selected row (or $0$ if nothing has been selected yet). For the convenience of implementation, $p[0]$ is assumed to be equal to the number of the current row.
The array $minv[1 \ldots m]$ contains, for each column $j$ , the auxiliary minima necessary for a quick recalculation of the potential, as described above.
The array $way[1 \ldots m]$ contains information about where these minimums are reached so that we can later reconstruct the augmenting path. Note that, to reconstruct the path, it is sufficient to store only column values, since the row numbers can be taken from the matching (i.e., from the array $p$ ). Thus, $way[j]$ , for each column $j$ , contains the number of the previous column in the path (or $0$ if there is none).
The algorithm itself is an outer loop through the rows of the matrix , inside which the $i$ -th row of the matrix is considered. The first do-while loop runs until a free column $j0$ is found. Each iteration of the loop marks visited a new column with the number $j0$ (calculated at the last iteration; and initially equal to zero - i.e. we start from a dummy column), as well as a new row $i0$ - adjacent to it in the matching (i.e. $p[j0]$ ; and initially when $j0=0$ the $i$ -th row is taken). Due to the appearance of a new visited row $i0$ , you need to recalculate the array $minv$ and $\Delta$ accordingly. If $\Delta$ is updated, then the column $j1$ becomes the minimum that has been reached (note that with such an implementation $\Delta$ could turn out to be equal to zero, which means that the potential cannot be changed at the current step: there is already a new reachable column). After that, the potential and the $minv$ array are recalculated. At the end of the "do-while" loop, we found an augmenting path ending in a column $j0$ that can be "unrolled" using the ancestor array $way$ .
The constant INF is "infinity", i.e. some number, obviously greater than all possible numbers in the input matrix $A$ .
To restore the answer in a more familiar form, i.e. finding for each row $i = 1 \ldots n$ the number $ans[i]$ of the column selected in it, can be done as follows:
The cost of the matching can simply be taken as the potential of the zero column (taken with the opposite sign). Indeed, as you can see from the code, $-v[0]$ contains the sum of all the values of $\Delta$ , i.e. total change in potential. Although several values of $u[i]$ and $v[j]$ could change at once, the total change in the potential is exactly equal to $\Delta$ , since until there is an augmenting path, the number of reachable rows is exactly one more than the number of the reachable columns (only the current row $i$ does not have a "pair" in the form of a visited column):
Connection to the Successive Shortest Path Algorithm ¶
The Hungarian algorithm can be seen as the Successive Shortest Path Algorithm , adapted for the assignment problem. Without going into the details, let's provide an intuition regarding the connection between them.
The Successive Path algorithm uses a modified version of Johnson's algorithm as reweighting technique. This one is divided into four steps:
- Use the Bellman-Ford algorithm, starting from the sink $s$ and, for each node, find the minimum weight $h(v)$ of a path from $s$ to $v$ .
For every step of the main algorithm:
- Reweight the edges of the original graph in this way: $w(u,v) \gets w(u,v)+h(u)-h(v)$ .
- Use Dijkstra 's algorithm to find the shortest-paths subgraph of the original network.
- Update potentials for the next iteration.
Given this description, we can observe that there is a strong analogy between $h(v)$ and potentials: it can be checked that they are equal up to a constant offset. In addition, it can be shown that, after reweighting, the set of all zero-weight edges represents the shortest-path subgraph where the main algorithm tries to increase the flow. This also happens in the Hungarian algorithm: we create a subgraph made of rigid edges (the ones for which the quantity $A[i][j]-u[i]-v[j]$ is zero), and we try to increase the size of the matching.
In step 4, all the $h(v)$ are updated: every time we modify the flow network, we should guarantee that the distances from the source are correct (otherwise, in the next iteration, Dijkstra's algorithm might fail). This sounds like the update performed on the potentials, but in this case, they are not equally incremented.
To deepen the understanding of potentials, refer to this article .
Task examples ¶
Here are a few examples related to the assignment problem, from very trivial to less obvious tasks:
Given a bipartite graph, it is required to find in it the maximum matching with the minimum weight (i.e., first of all, the size of the matching is maximized, and secondly, its cost is minimized). To solve it, we simply build an assignment problem, putting the number "infinity" in place of the missing edges. After that, we solve the problem with the Hungarian algorithm, and remove edges of infinite weight from the answer (they could enter the answer if the problem does not have a solution in the form of a perfect matching).
Given a bipartite graph, it is required to find in it the maximum matching with the maximum weight . The solution is again obvious, all weights must be multiplied by minus one.
The task of detecting moving objects in images : two images were taken, as a result of which two sets of coordinates were obtained. It is required to correlate the objects in the first and second images, i.e. determine for each point of the second image, which point of the first image it corresponded to. In this case, it is required to minimize the sum of distances between the compared points (i.e., we are looking for a solution in which the objects have taken the shortest path in total). To solve, we simply build and solve an assignment problem, where the weights of the edges are the Euclidean distances between points.
The task of detecting moving objects by locators : there are two locators that can't determine the position of an object in space, but only its direction. Both locators (located at different points) received information in the form of $n$ such directions. It is required to determine the position of objects, i.e. determine the expected positions of objects and their corresponding pairs of directions in such a way that the sum of distances from objects to direction rays is minimized. Solution: again, we simply build and solve the assignment problem, where the vertices of the left part are the $n$ directions from the first locator, the vertices of the right part are the $n$ directions from the second locator, and the weights of the edges are the distances between the corresponding rays.
Covering a directed acyclic graph with paths : given a directed acyclic graph, it is required to find the smallest number of paths (if equal, with the smallest total weight) so that each vertex of the graph lies in exactly one path. The solution is to build the corresponding bipartite graph from the given graph and find the maximum matching of the minimum weight in it. See separate article for more details.
Tree coloring book . Given a tree in which each vertex, except for leaves, has exactly $k-1$ children. It is required to choose for each vertex one of the $k$ colors available so that no two adjacent vertices have the same color. In addition, for each vertex and each color, the cost of painting this vertex with this color is known, and it is required to minimize the total cost. To solve this problem, we use dynamic programming. Namely, let's learn how to calculate the value $d[v][c]$ , where $v$ is the vertex number, $c$ is the color number, and the value $d[v][c]$ itself is the minimum cost needed to color all the vertices in the subtree rooted at $v$ , and the vertex $v$ itself with color $c$ . To calculate such a value $d[v][c]$ , it is necessary to distribute the remaining $k-1$ colors among the children of the vertex $v$ , and for this, it is necessary to build and solve the assignment problem (in which the vertices of the left part are colors, the vertices of the right part are children, and the weights of the edges are the corresponding values of $d$ ). Thus, each value $d[v][c]$ is calculated using the solution of the assignment problem, which ultimately gives the asymptotic $\mathcal{O}(nk^4)$ .
If, in the assignment problem, the weights are not on the edges, but on the vertices, and only on the vertices of the same part , then it's not necessary to use the Hungarian algorithm: just sort the vertices by weight and run the usual Kuhn algorithm (for more details, see a separate article ).
Consider the following special case . Let each vertex of the left part be assigned some number $\alpha[i]$ , and each vertex of the right part $\beta[j]$ . Let the weight of any edge $(i,j)$ be equal to $\alpha[i]\cdot \beta[j]$ (the numbers $\alpha[i]$ and $\beta[j]$ are known). Solve the assignment problem. To solve it without the Hungarian algorithm, we first consider the case when both parts have two vertices. In this case, as you can easily see, it is better to connect the vertices in the reverse order: connect the vertex with the smaller $\alpha[i]$ to the vertex with the larger $\beta[j]$ . This rule can be easily generalized to an arbitrary number of vertices: you need to sort the vertices of the first part in increasing order of $\alpha[i]$ values, the second part in decreasing order of $\beta[j]$ values, and connect the vertices in pairs in that order. Thus, we obtain a solution with complexity of $\mathcal{O}(n\log n)$ .
The Problem of Potentials . Given a matrix $A[1 \ldots n][1 \ldots m]$ , it is required to find two arrays $u[1 \ldots n]$ and $v[1 \ldots m]$ such that, for any $i$ and $j$ , $u[i] + v[j] \leq a[i][j]$ and the sum of elements of arrays $u$ and $v$ is maximum. Knowing the Hungarian algorithm, the solution to this problem will not be difficult: the Hungarian algorithm just finds such a potential $u, v$ that satisfies the condition of the problem. On the other hand, without knowledge of the Hungarian algorithm, it seems almost impossible to solve such a problem.
This task is also called the dual problem of the assignment problem: minimizing the total cost of the assignment is equivalent to maximizing the sum of the potentials.
Literature ¶
Ravindra Ahuja, Thomas Magnanti, James Orlin. Network Flows [1993]
Harold Kuhn. The Hungarian Method for the Assignment Problem [1955]
James Munkres. Algorithms for Assignment and Transportation Problems [1957]
Practice Problems ¶
UVA - Crime Wave - The Sequel
UVA - Warehouse
SGU - Beloved Sons
UVA - The Great Wall Game
UVA - Jogging Trails
- Alessandro Minisini (92.97%)
- Oleksandr Kulkov (7.03%)
Index Assignment problem Hungarian algorithm Solve online

The assignment problem
The assignment problem deals with assigning machines to tasks, workers to jobs, soccer players to positions, and so on. The goal is to determine the optimum assignment that, for example, minimizes the total cost or maximizes the team effectiveness. The assignment problem is a fundamental problem in the area of combinatorial optimization.
Assume for example that we have four jobs that need to be executed by four workers. Because each worker has different skills, the time required to perform a job depends on the worker who is assigned to it.
The matrix below shows the time required (in minutes) for each combination of a worker and a job. The jobs are denoted by J1, J2, J3, and J4, the workers by W1, W2, W3, and W4.
| 82 | 83 | 69 | 92 | |
| 77 | 37 | 49 | 92 | |
| 11 | 69 | 5 | 86 | |
| 8 | 9 | 98 | 23 |
Each worker should perform exactly one job and the objective is to minimize the total time required to perform all jobs.
It turns out to be optimal to assign worker 1 to job 3, worker 2 to job 2, worker 3 to job 1 and worker 4 to job 4. The total time required is then 69 + 37 + 11 + 23 = 140 minutes. All other assignments lead to a larger amount of time required.
The Hungarian algorithm can be used to find this optimal assignment. The steps of the Hungarian algorithm can be found here , and an explanation of the Hungarian algorithm based on the example above can be found here .
HungarianAlgorithm.com © 2013-2024
Hungarian Method: Assignment Problem
Hungarian Method is an efficient method for solving assignment problems .
This method is based on the following principle:
- If a constant is added to, or subtracted from, every element of a row and/or a column of the given cost matrix of an assignment problem, the resulting assignment problem has the same optimal solution as the original problem.
Hungarian Algorithm
The objective of this section is to examine a computational method - an algorithm - for deriving solutions to the assignment problems. The following steps summarize the approach:
Steps in Hungarian Method
1. Identify the minimum element in each row and subtract it from every element of that row.
2. Identify the minimum element in each column and subtract it from every element of that column.
3. Make the assignments for the reduced matrix obtained from steps 1 and 2 in the following way:
- For every zero that becomes assigned, cross out (X) all other zeros in the same row and the same column.
- If for a row and a column, there are two or more zeros and one cannot be chosen by inspection, then you are at liberty to choose the cell arbitrarily for assignment.
4. An optimal assignment is found, if the number of assigned cells equals the number of rows (and columns). In case you have chosen a zero cell arbitrarily, there may be alternate optimal solutions. If no optimal solution is found, go to step 5.
5. Draw the minimum number of vertical and horizontal lines necessary to cover all the zeros in the reduced matrix obtained from step 3 by adopting the following procedure:
- Mark all the rows that do not have assignments.
- Mark all the columns (not already marked) which have zeros in the marked rows.
- Mark all the rows (not already marked) that have assignments in marked columns.
- Repeat steps 5 (i) to (iii) until no more rows or columns can be marked.
- Draw straight lines through all unmarked rows and marked columns.
You can also draw the minimum number of lines by inspection.
6. Select the smallest element from all the uncovered elements. Subtract this smallest element from all the uncovered elements and add it to the elements, which lie at the intersection of two lines. Thus, we obtain another reduced matrix for fresh assignment.
7. Go to step 3 and repeat the procedure until you arrive at an optimal assignment.
For the time being we assume that number of jobs is equal to number of machines or persons. Later in the chapter, we will remove this restrictive assumption and consider a special case where no. of facilities and tasks are not equal.
Share This Article
Operations Research Simplified Back Next
Goal programming Linear programming Simplex Method Transportation Problem
Formation construction and reconfiguration control of UAV swarms: a perspective from distributed assignment and optimization
- Original Paper
- Published: 26 August 2024
Cite this article

- Jiangyuan Tian ORCID: orcid.org/0000-0002-4770-6524 1 ,
- Ruixuan Wei 2 &
- Longting Jiang 1
28 Accesses
Explore all metrics
This article proposes a framework for the swarm of unmanned aerial vehicles (UAVs) to swiftly construct a formation. The framework also enables the swarm to reconfigure the formation effectively in a distributed way when the number of UAVs changes. Different from the classic formation methods, we endow each UAV with an objective function and an assignment vector. Then, a novel distributed optimization protocol is designed for the formation construction, which enables the swarm to construct the desired formation within a prescribed time. The formation needs to be reconfigured when some UAVs leave or join the swarm. A distributed assignment protocol is raised for the reconfiguration problem, which aims at reassigning the relative positions for the UAVs and reconfiguring the swarm formation. This article integrates these two protocols into one framework, where the transition between the formation construction and its reconfiguration is smooth. The distributed design of the framework improves the individual UAV’s decision-making ability. We further give the proofs of consensus and optimality of the two protocols. The simulation results confirm the effectiveness of the framework.
This is a preview of subscription content, log in via an institution to check access.
Access this article
Subscribe and save.
- Get 10 units per month
- Download Article/Chapter or eBook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
Price includes VAT (Russian Federation)
Instant access to the full article PDF.
Rent this article via DeepDyve
Institutional subscriptions
Similar content being viewed by others

Distributed Formation Control and Collision Avoidance for Heterogeneous UAV Swarm

No-reference Path Receding Horizon Control for Multi-UAV Formation Reconfiguration Based on Adaptive Differential Evolution

Consensus-Based Algorithms for Controlling Swarms of Unmanned Aerial Vehicles
Explore related subjects.
- Automotive Engineering
Code Availability
The code during the current study are not publicly available but are available from the first author on reasonable request.
Data availability
The datas in this paper are availability under request.
Hayat, S., Yanmaz, E., Muzaffar, R.: Survey on unmanned aerial vehicle networks for civil applications: a communications viewpoint. IEEE Commun. Surv. Tutor. 18 (4), 2624–2661 (2016). https://doi.org/10.1109/COMST.2016.2560343
Article Google Scholar
Mozaffari, M., Saad, W., Bennis, M., Nam, Y.-H., Debbah, M.: A tutorial on UAVS for wireless networks: applications, challenges, and open problems. IEEE Commun. Surv. Tutor. 21 (3), 2334–2360 (2019). https://doi.org/10.1109/COMST.2019.2902862
Zhao, B., Xian, B., Zhang, Y., Zhang, X.: Nonlinear robust adaptive tracking control of a quadrotor UAV via immersion and invariance methodology. IEEE Trans. Ind. Electron. 62 (5), 2891–2902 (2015). https://doi.org/10.1109/TIE.2014.2364982
Wu, J., Luo, C., Luo, Y., Li, K.: Distributed UAV swarm formation and collision avoidance strategies over fixed and switching topologies. IEEE Trans. Cybern. 52 (10), 10969–10979 (2022). https://doi.org/10.1109/TCYB.2021.3132587
Shakhatreh, H., Sawalmeh, A.H., Al-Fuqaha, A., Dou, Z., Almaita, E., Khalil, I., Othman, N.S., Khreishah, A., Guizani, M.: Unmanned aerial vehicles (UAVS): a survey on civil applications and key research challenges. IEEE Access 7 , 48572–48634 (2019). https://doi.org/10.1109/ACCESS.2019.2909530
Iscold, P., Pereira, G.A.S., Torres, L.A.B.: Development of a hand-launched small UAV for ground reconnaissance. IEEE Trans. Aerosp. Electron. Syst. 46 (1), 335–348 (2010). https://doi.org/10.1109/TAES.2010.5417166
Wang, T., Li, M., Zhang, M.-Y.: Cooperative coverage reconnaissance of multi-UAV. In: 2020 IEEE 5th Information Technology and Mechatronics Engineering Conference (ITOEC), pp. 1647–1651. IEEE, Chongqing (2020). https://doi.org/10.1109/ITOEC49072.2020.9141873
Zhou, L., Leng, S., Liu, Q., Wang, Q.: Intelligent UAV swarm cooperation for multiple targets tracking. IEEE Internet Things J. 9 (1), 743–754 (2022). https://doi.org/10.1109/JIOT.2021.3085673
Wang, X., Zhou, W., Wang, X.: Research on multi-UAV cooperative tracking target based on PSO predictive control algorithm. IOP Conf. Ser. Mater. Sci. Eng. 646 (1), 012038 (2019). https://doi.org/10.1088/1757-899X/646/1/012038
Xu, Y., Ren, G., Chen, J., Zhang, X., Jia, L., Kong, L.: Interference-aware cooperative anti-jamming distributed channel selection in UAV communication networks. Appl. Sci. 8 (10), 1911 (2018). https://doi.org/10.3390/app8101911
Duan, H., Huo, M., Yang, Z., Shi, Y., Luo, Q.: Predator-prey pigeon-inspired optimization for UAV ALS longitudinal parameters tuning. IEEE Trans. Aerosp. Electron. Syst. 55 (5), 2347–2358 (2019). https://doi.org/10.1109/TAES.2018.2886612
Xing, D., Zhen, Z., Gong, H.: Offense-defense confrontation decision making for dynamic UAV swarm versus UAV swarm. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 233 (15), 5689–5702 (2019). https://doi.org/10.1177/0954410019853982
Liu, X., Ansari, N.: Resource allocation in UAV-assisted m2m communications for disaster rescue. IEEE Wirel. Commun. Lett. 8 (2), 580–583 (2019). https://doi.org/10.1109/LWC.2018.2880467
Ouyang, Q., Wu, Z., Cong, Y., Wang, Z.: Formation control of unmanned aerial vehicle swarms: a comprehensive review. Asian J. Control 25 (1), 570–593 (2023). https://doi.org/10.1002/asjc.2806
Kim, M.-H., Baik, H., Lee, S.: Response threshold model based UAV search planning and task allocation. J. Intell. Robot. Syst. 75 (3–4), 625–640 (2014). https://doi.org/10.1007/s10846-013-9887-6
Malvankar-Mehta, M.S., Mehta, S.S.: Optimal task allocation in multi-human multi-robot interaction. Optim. Lett. 9 (8), 1787–1803 (2015). https://doi.org/10.1007/s11590-015-0890-7
Article MathSciNet Google Scholar
Zhang, X., Duan, H.: An improved constrained differential evolution algorithm for unmanned aerial vehicle global route planning. Appl. Soft Comput. 26 , 270–284 (2015). https://doi.org/10.1016/j.asoc.2014.09.046
Liang, X., Meng, G., Luo, H., Chen, X.: Dynamic path planning based on improved boundary value problem for unmanned aerial vehicle. Clust. Comput. 19 (4), 2087–2096 (2016). https://doi.org/10.1007/s10586-016-0650-1
Lau, S.Y., Naeem, W.: Co-operative tensegrity-based formation control algorithm for a multi-aircraft system. In: 2015 American Control Conference (ACC), pp. 750–756. IEEE, Chicago (2015). https://doi.org/10.1109/ACC.2015.7170824
Liao, F., Teo, R., Wang, J.L., Dong, X., Lin, F., Peng, K.: Distributed formation and reconfiguration control of VTOL UAVs. IEEE Trans. Control Syst. Technol. 25 (1), 270–277 (2017). https://doi.org/10.1109/TCST.2016.2547952
Dong, X., Yu, B., Shi, Z., Zhong, Y.: Time-varying formation control for unmanned aerial vehicles: theories and applications. IEEE Trans. Control Syst. Technol. 23 (1), 340–348 (2015). https://doi.org/10.1109/TCST.2014.2314460
Li, N.H.M., Liu, H.H.T.: Formation UAV flight control using virtual structure and motion synchronization. In: 2008 American Control Conference, pp. 1782–1787. IEEE, Seattle (2008). https://doi.org/10.1109/ACC.2008.4586750
Xu, J., Guo, Q., Xiao, L., Chen, G., Guan, X.: An autonomous planning method for UAV based on behavior-conditional model. In: 2019 IEEE 7th International Conference on Computer Science and Network Technology (ICCSNT), pp. 255–261. IEEE, Dalian (2019). https://doi.org/10.1109/ICCSNT47585.2019.8962520
Ge, X., Han, Q.-L.: Distributed formation control of networked multi-agent systems using a dynamic event-triggered communication mechanism. IEEE Trans. Ind. Electron. 64 (10), 8118–8127 (2017). https://doi.org/10.1109/TIE.2017.2701778
You, K., Xie, L.: Network topology and communication data rate for consensusability of discrete-time multi-agent systems. IEEE Trans. Autom. Control 56 (10), 2262–2275 (2011). https://doi.org/10.1109/TAC.2011.2164017
Yang, T., Yi, X., Wu, J., Yuan, Y., Wu, D., Meng, Z., Hong, Y., Wang, H., Lin, Z., Johansson, K.H.: A survey of distributed optimization. Annu. Rev. Control. 47 , 278–305 (2019). https://doi.org/10.1016/j.arcontrol.2019.05.006
Molzahn, D.K., Dorfler, F., Sandberg, H., Low, S.H., Chakrabarti, S., Baldick, R., Lavaei, J.: A survey of distributed optimization and control algorithms for electric power systems. IEEE Trans. Smart Grid 8 (6), 2941–2962 (2017). https://doi.org/10.1109/TSG.2017.2720471
Lin, Z., Liu, H.H.T.: Topology-based distributed optimization for multi-UAV cooperative wildfire monitoring: topology-based distributed optimization for multi-UAV cooperative wildfire monitoring. Opt. Control Appl. Methods 39 (4), 1530–1548 (2018). https://doi.org/10.1002/oca.2424
Rajasree, R., Jisha, V.R.: Optimal formation control of unmanned aerial vehicles with reconfiguration. In: 2015 International Conference on Control Communication & Computing India (ICCC), pp. 36–41. IEEE, Trivandrum (2015). https://doi.org/10.1109/ICCC.2015.7432866
Zhang, H., Zhao, G., Xu, G.: Time-optimal control for formation reconfiguration of multiple unmanned aerial vehicles. In: 2016 35th Chinese Control Conference (CCC), pp. 5630–5635. IEEE, Chengdu (2016). https://doi.org/10.1109/ChiCC.2016.7554234
Sperandio Giacomin, P.A., Hemerly, E.M.: Reconfiguration between longitudinal and circular formations for multi-UAV systems by using segments. J. Intell. Robot. Syst. 78 (2), 339–355 (2015). https://doi.org/10.1007/s10846-014-0063-4
Zhou, Y., Rao, B., Wang, W.: UAV swarm intelligence: recent advances and future trends. IEEE Access 8 , 183856–183878 (2020). https://doi.org/10.1109/ACCESS.2020.3028865
Godsil, C., Royle, G.: Algebraic Graph Theory. Graduate Texts in Mathematics, vol. 207. Springer, New York (2001). https://doi.org/10.1007/978-1-4613-0163-9
Book Google Scholar
Zhang, F.: Matrix Theory: Basic Results and Techniques. Springer, New York (2011). https://doi.org/10.1007/978-1-4614-1099-7
Li, T., Li, Y., Qian, Y.: Improved Hungarian algorithm for assignment problems of serial-parallel systems. J. Syst. Eng. Electron. 27 (4), 858–870 (2016). https://doi.org/10.21629/JSEE.2016.04.14
Ding, C., Shi, C., Chen, Y.: Nonsingular prescribed-time stabilization of a class of uncertain nonlinear systems: a novel coordinate mapping method. Int. J. Robust Nonlinear Control 30 (9), 3566–3581 (2020). https://doi.org/10.1002/rnc.4949
Download references
Acknowledgements
This work was supported in part by Science and Technology Innovation 2030-Key Project of “New Generation Artificial Intelligence” under grant 2018AAA0102403. National Natural Science Foundation of China underGrant 61573373.
Author information
Authors and affiliations.
Graduate College, Air Force Engineering University, Baqiao, Xi’an, 710038, Shaanxi, China
Jiangyuan Tian & Longting Jiang
Aeronautics Engineering College, Air Force Engineering University, Baqiao, Xi’an, 710038, Shaanxi, China
Ruixuan Wei
You can also search for this author in PubMed Google Scholar
Contributions
All authors contributed to the study conception and design. The manuscript was written by Jiangyuan Tian. All authors read and approved the manuscript.
Corresponding author
Correspondence to Ruixuan Wei .
Ethics declarations
Conflict of interest.
The authors declare that they have no Conflict of interest.
Ethical standards
This manuscript is in compliance with ethical standards.
Additional information
Publisher's note.
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This appendix gives an extension of the simulation in the 3-dimensional scenario.
Although the result in the Fig. 16 illustrates that our method can make the UAVs track the mobile locating points and construct the formation within the prescribed time, the crossed trajectories in the 2-dimensional space still reflect that there is a latent risk of collisions between UAVs. In order to eliminate this risk, we extend the space to 3-dimension. The \(X-Y\) plane is for the formation mission and the introduction of the Z direction provides us with an additional dimension for collision avoidance between UAVs.
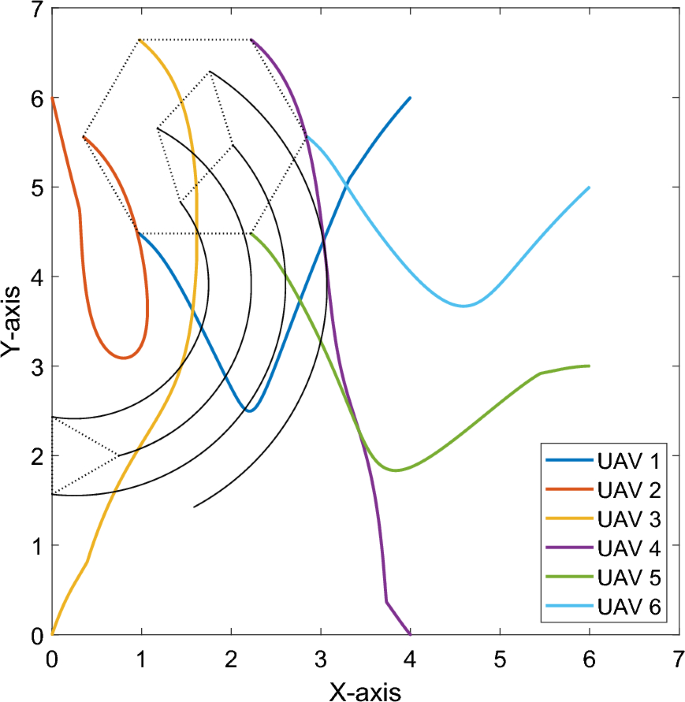
Trajectories of UAVs
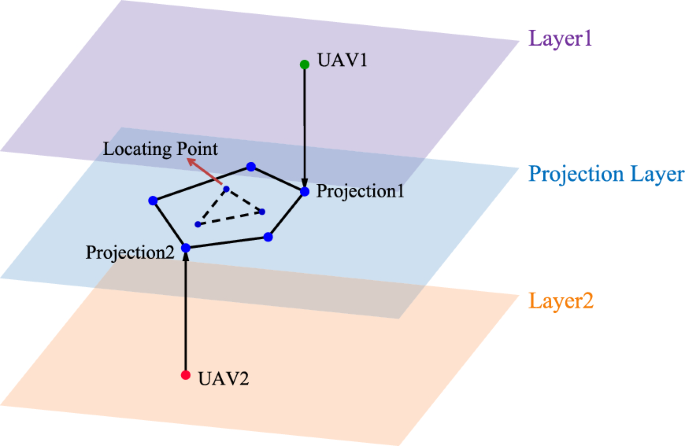
Projection of UAVs
As is shown in the Fig. 17 , the locating points as well as the final formation are in the projection layer. The UAVs are initialized in different layers. Then the whole mission can be devided in 2 independent control problems: the control of the UAVs’ projections to construct the formation and the control of the Z coordinate to make the UAVs reach the projection layer. We have proposed our method for the first control problem in the previous article. Next we commence solving the second control problem.
Without causing any ambiguity, in this appendix we denote the Z coordinate of the i th UAV and the projection layer as \(z_i\) and \(z_d\) respectively. Then we propose a control protocol for the i th UAV to drive it to the projection layer:
Obviously, with the application of the protocol described in Eq. A1 , \(z_i\) will reach \(z_d\) as \(t\rightarrow \infty \) . Then we prove that the protocol described in Eq. A1 can also realize the collision avoidance between UAVs.
For \(\forall i,j\in \left\{ 1,2,\ldots ,n \right\} ,i\ne j\) , if \(z_i(0) > z_j(0)\) , then we have \(z_i(t) \ge z_j(t)\) for \(\forall t\ge 0\) and the equal sign is taken when \(t\rightarrow \infty \) .
Let \(F(t)=z_i(t)-z_j(t)\) . Take the derivative of F ( t ), we have:
Solve the differential equation A2 and take the initial condition into consideration, we have
It indicates that F ( t ) is a monotonic decreasing function and \(F(t) \ge 0\) for \(\forall t\ge 0\) . \(\square \)
The Theorem 3 implies that if the initial Z coordinate of the UAV i is greater than that of the UAV j , then during the whole formation process, the UAV i will be above the UAV j all the time until they both reach the projection layer in the end. We can realize the collision avoidance through guaranteeing that different UAVs will have different Z coordinates at the same time.
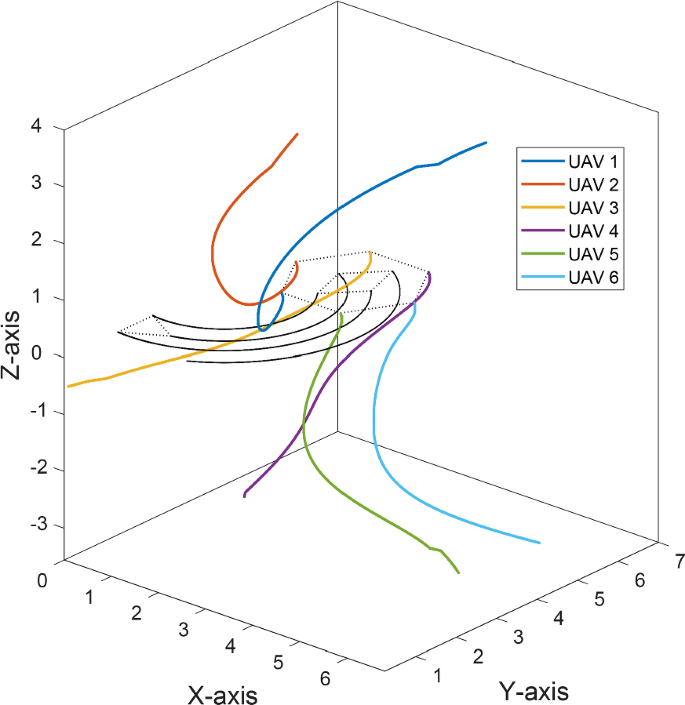
Trajectories of UAVs in 3-dimensional space
Then we give the simulation of the Sect. 4.3 in 3-dimensional space. All the simulation conditions, parameters and dynamic equations are the same as those in the Sect. 4.3 . The only difference is the Z coordinate needs to be added into the position information. The Z coordinate of the projection layer is set as 0. The initial Z coordinates of the 6 UAVs are set as 3, 2, \(-0.5\) , \(-1.5\) , \(-3\) , \(-3.5\) respectively. The simulation result is demonstrated in the Fig. 18 . From the result we can see that the trajectories of the UAVs don’t cross with each other. The Fig. 18 illustrates that with the addition of the Z direction and the application of the protocol described in Eq. A1 , the UAVs can construct the formation without the risk of collisions.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
Reprints and permissions
About this article
Tian, J., Wei, R. & Jiang, L. Formation construction and reconfiguration control of UAV swarms: a perspective from distributed assignment and optimization. Nonlinear Dyn (2024). https://doi.org/10.1007/s11071-024-10024-z
Download citation
Received : 25 June 2023
Accepted : 10 July 2024
Published : 26 August 2024
DOI : https://doi.org/10.1007/s11071-024-10024-z
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Unmanned aerial vehicle swarm
- Formation control
- Formation reconfiguration
- Distributed assignment
- Distributed optimization
- Find a journal
- Publish with us
- Track your research

IMAGES
COMMENTS
The Hungarian algorithm, aka Munkres assignment algorithm, utilizes the following theorem for polynomial runtime complexity ( worst case O (n3)) and guaranteed optimality: If a number is added to or subtracted from all of the entries of any one row or column of a cost matrix, then an optimal assignment for the resulting cost matrix is also an ...
Hungarian algorithm The Hungarian method is a combinatorial optimization algorithm that solves the assignment problem in polynomial time and which anticipated later primal-dual methods. It was developed and published in 1955 by Harold Kuhn, who gave it the name "Hungarian method" because the algorithm was largely based on the earlier works of two Hungarian mathematicians, Dénes Kőnig and ...
The Hungarian method is a computational optimization technique that addresses the assignment problem in polynomial time and foreshadows following primal-dual alternatives.
Hungarian Method Examples Now we will examine a few highly simplified illustrations of Hungarian Method for solving an assignment problem. Later in the chapter, you will find more practical versions of assignment models like Crew assignment problem, Travelling salesman problem, etc.
Hungarian method for assignment problem Step 1. Subtract the entries of each row by the row minimum.
The Hungarian algorithm: An example We consider an example where four jobs (J1, J2, J3, and J4) need to be executed by four workers (W1, W2, W3, and W4), one job per worker. The matrix below shows the cost of assigning a certain worker to a certain job. The objective is to minimize the total cost of the assignment.
Also, our problem is a special case of binary integer linear programming problem (which is NP-hard). But, due to the specifics of the problem, there are more efficient algorithms to solve it. We'll handle the assignment problem with the Hungarian algorithm (or Kuhn-Munkres algorithm).
In this lesson we learn what is an assignment problem and how we can solve it using the Hungarian method.
THE HUNGARIAN METHOD FOR THE ASSIGNMENT. PROBLEM'. H. W. Kuhn. Bryn Y a w College. Assuming that numerical scores are available for the perform- ance of each of n persons on each of n jobs, the "assignment problem" is the quest for an assignment of persons to jobs so that the sum of the. n scores so obtained is as large as possible.
1. INTRODUCTION The Hungarian Method [ 11 is an algorithm for solving assignment problems that is based on the work of D. Konig and J. Egervgry. In one possible interpretation, an assignment problem asks for the best assignment of a set of persons to a set of jobs, where the feasible assignments are ranked by the total scores or ratings of the ...
The Hungarian method, also known as the Kuhn-Munkres algorithm, is a computational technique used to solve the assignment problem in polynomial time. It's a precursor to many primal-dual methods used today.
For implementing the above algorithm, the idea is to use the max_cost_assignment () function defined in the dlib library. This function is an implementation of the Hungarian algorithm (also known as the Kuhn-Munkres algorithm) which runs in O (N3) time.
The Hungarian algorithm The Hungarian algorithm consists of the four steps below. The first two steps are executed once, while Steps 3 and 4 are repeated until an optimal assignment is found. The input of the algorithm is an n by n square matrix with only nonnegative elements.
The Hungarian method is a combinatorial optimization algorithm which solves the assignment problem in polynomial time Later it was discovered that it was a primal-dual Simplex method .
Solve an assignment problem online Fill in the cost matrix of an assignment problem and click on 'Solve'. The optimal assignment will be determined and a step by step explanation of the hungarian algorithm will be given.
Textbooks: https://amzn.to/2VgimyJ https://amzn.to/2CHalvx https://amzn.to/2Svk11k In this video, we'll talk about how to solve a special case of the transportation problem called the assignment ...
Here is the video about assignment problem - Hungarian method with algorithm.NOTE: After row and column scanning, If you stuck with more than one zero in th...
The Assignment Problem and the Hungarian Method Example 1: You work as a sales manager for a toy manufacturer, and you currently have three salespeople on the road meeting buyers. Your salespeople are in Austin, TX; Boston, MA; and Chicago, IL. You want them to fly to three other cities: Denver, CO; Edmonton, Alberta; and Fargo, ND.
The Hungarian algorithm can be seen as the Successive Shortest Path Algorithm, adapted for the assignment problem. Without going into the details, let's provide an intuition regarding the connection between them. The Successive Path algorithm uses a modified version of Johnson's algorithm as reweighting technique.
This paper has always been one of my favorite “children,” combining as it does elements of the duality of linear programming and combinatorial tools from graph theory. It may be of some interest to tell the story of its origin.
The assignment problem deals with assigning machines to tasks, workers to jobs, soccer players to positions, and so on. The goal is to determine the optimum assignment that, for example, minimizes the total cost or maximizes the team effectiveness. The assignment problem is a fundamental problem in the area of combinatorial optimization.
Hungarian Method is an efficient method for solving assignment problems. This method is based on the following principle: If a constant is added to, or subtracted from, every element of a row and/or a column of the given cost matrix of an assignment problem, the resulting assignment problem has the same optimal solution as the original problem.
This article proposes a distributed assignment and optimization method for the formation construction and reconfiguration control of the UAV swarm. Based on the classical Hungarian algorithm for the assignment problem, we remodel the problem in a distributed way and design an distributed assignment protocol described in Eq. 12. By virtue of the ...
📒⏩Comment Below If This Video Helped You 💯Like 👍 & Share With Your Classmates - ALL THE BEST 🔥Do Visit My Second Channel - https://bit.ly/3rMGcSAThis vi...
[12]H. W. Kuhn, The hungarian method for the assignment problem, Naval Research Logistics Quarterly 2 (1955) 83-97. [13]S. Giordani, M. Lujak, F. Martinelli, A distributed multi-agent production planning and scheduling framework for mobile robots, Computers & Industrial Engineering 64 (2013) 19-30.